加油！一定能找到好工作！

模型评估

模型评估常用方法

一般情况来说，单一评分标准无法完全评估一个机器学习模型。只用good和bad偏离真实场景去评估某个模型，都是一种欠妥的评估方式。下面介绍常用的分类模型和回归模型评估方法。

分类模型常用评估方法：

指标	描述
Accuracy	准确率
Precision	精准度/查准率
Recall	召回率/查全率
P-R曲线	查准率为纵轴，查全率为横轴，作图
F1	F1值
Confusion Matrix	混淆矩阵
ROC	ROC曲线
AUC	ROC曲线下的面积

F1 是基于查准率与查全率的调和平均(harmonic mean)定义的： $\frac{1}{F 1}=\frac{1}{2} \cdot\left(\frac{1}{P}+\frac{1}{R}\right)$
\[ F 1=\frac{2 \times P \times R}{P+R} = =\frac{2 \times TP }{样例总数 + TP - TN} \]
用于综合考虑查准率、查全率的性能度量。

回归模型常用评估方法：

指标	描述
Mean Square Error (MSE, RMSE)	均方误差
Absolute Error (MAE, RAE)	绝对误差
R-Squared	R平方值

机器学习中的Bias和Variance有什么区别和联系

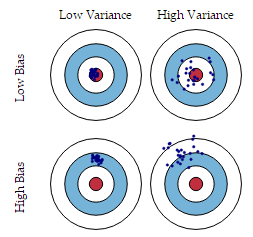
Bias(偏差)与Variance(方差)分别是用于衡量一个模型泛化误差的两个方面
- Bias(偏差)： 指的是模型预测的期望值与真实值之间的差（描述模型的拟合能力）
- Variance(方差)： 指的是模型预测的期望值与预测值之间的差的平方和（描述模型的稳定性）

在监督学习中，模型的泛化误差可分解为偏差、方差与噪声之和。

\[ Err(x) = Bias^2 + Variance + Irreducible\ Error \]

噪声：表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度

经验误差与泛化误差

经验误差（empirical error）：也叫训练误差（training error），模型在训练集上的误差。
泛化误差（generalization error）：模型在新样本集（测试集）上的误差。

深度学习中的偏差与方差

神经网络的拟合能力非常强，因此它的训练误差（偏差）通常较小；
但是过强的拟合能力会导致较大的方差，使模型的测试误差（泛化误差）增大；
因此深度学习的核心工作之一就是研究如何降低模型的泛化误差，这类方法统称为正则化方法。

偏差方差与Boosting和Bagging联系

Boosting 能提升弱分类器性能的原因是降低了偏差
Bagging 则是降低了方差

Boosting 方法：
Boosting 的基本思路就是在不断减小模型的训练误差（拟合残差或者加大错类的权重），加强模型的学习能力，从而减小偏差；
但 Boosting 不会显著降低方差，因为其训练过程中各基学习器是强相关的，缺少独立性。
Bagging 方法：
对 n 个独立不相关的模型预测结果取平均，方差是原来的 1/n；
假设所有基分类器出错的概率是独立的，超过半数基分类器出错的概率会随着基分类器的数量增加而下降。

偏差与方差的计算公式

记在训练集 D 上学得的模型为
\[ f(\boldsymbol{x} ; D) \]
模型的期望预测为
\[ \hat{f}(\boldsymbol{x})=\mathbb{E}_{D}[f(\boldsymbol{x} ; D)] \]
偏差（Bias）
\[ \operatorname{bias}^{2}(\boldsymbol{x})=(\hat{f}(\boldsymbol{x})-y)^{2} \]

偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力；

方差（Variance）
\[ \operatorname{var}(\boldsymbol{x})=\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\hat{f}(\boldsymbol{x}))^{2}\right] \]

方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响（模型的稳定性）；

噪声
\[ \varepsilon^{2}=\mathbb{E}_{D}\left[\left(y_{D}-y\right)^{2}\right] \]

噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。

“偏差-方差分解”表明模型的泛化能力是由算法的能力、数据的充分性、任务本身的难度共同决定的

偏差与方差的权衡（过拟合与模型复杂度的权衡）

给定学习任务，
当训练不足时，模型的拟合能力不够（数据的扰动不足以使模型产生显著的变化），此时偏差主导模型的泛化误差；
随着训练的进行，模型的拟合能力增强（模型能够学习数据发生的扰动），此时方差逐渐主导模型的泛化误差；
当训练充足后，模型的拟合能力过强（数据的轻微扰动都会导致模型产生显著的变化），此时即发生过拟合（训练数据自身的、非全局的特征也被模型学习了）
偏差和方差的关系和模型容量（模型复杂度）、欠拟合和过拟合的概念紧密相联
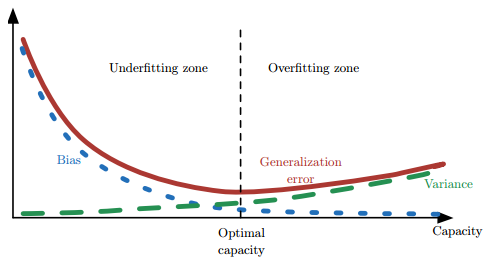
当模型的容量增大（x 轴）时，偏差（用点表示）随之减小，而方差（虚线）随之增大
沿着 x 轴存在最佳容量，小于最佳容量会呈现欠拟合，大于最佳容量会导致过拟合。

欠拟合与过拟合

欠拟合指模型不能在训练集上获得足够低的训练误差
过拟合指模型的训练误差与测试误差（泛化误差）之间差距过大
反映在评价指标上，就是模型在训练集上表现良好，但是在测试集和新数据上表现一般（泛化能力差）

根据不同的坐标方式，图解欠拟合与过拟合

横轴为训练样本数量，纵轴为误差

模型欠拟合：在训练集以及测试集上同时具有较高的误差，此时模型的偏差较大；
模型过拟合：在训练集上具有较低的误差，在测试集上具有较高的误差，此时模型的方差较大。
模型正常：在训练集以及测试集上，同时具有相对较低的偏差以及方差。

横轴为模型复杂程度，纵轴为误差

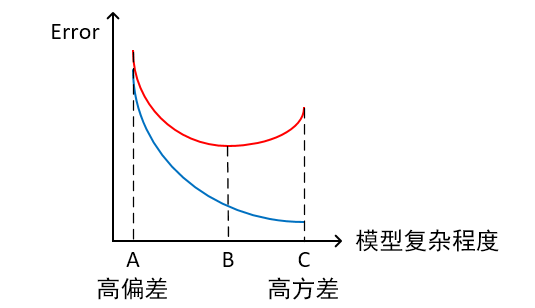
红线为测试集上的Error, 蓝线为训练集上的Error

模型欠拟合：模型在点A处，在训练集以及测试集上同时具有较高的误差，此时模型的偏差较大。
模型过拟合：模型在点C处，在训练集上具有较低的误差，在测试集上具有较高的误差，此时模型的方差较大。
模型正常：模型复杂程度控制在点B处为最优。

横轴为正则项系数，纵轴为误差

红线为测试集上的Error,蓝线为训练集上的Error

模型欠拟合：模型在点C处，在训练集以及测试集上同时具有较高的误差，此时模型的偏差较大。
模型过拟合：模型在点A处，在训练集上具有较低的误差，在测试集上具有较高的误差，此时模型的方差较大。
模型正常：模型复杂程度控制在点B处为最优。

降低过拟合的方法

数据增强
图像：平移、旋转、缩放
利用生成对抗网络（GAN）生成新数据
NLP：利用机器翻译生成新数据
增加正则化项（权值约束）
L1 正则化
L2 正则化
增大正则化项系数
降低模型复杂度
神经网络：减少网络层、神经元个数
决策树：降低树的深度、剪枝
采用Dropout方法
Dropout方法，通俗的讲就是在训练的时候让神经元以一定的概率不工作
提前终止 early stopping
集成学习
神经网络：Dropout
决策树：随机森林、GBDT

降低欠拟合的方法

加入新的特征
交叉特征、多项式特征、…
深度学习：因子分解机、Deep-Crossing、自编码器
增加模型复杂度
线性模型：添加高次项
神经网络：增加网络层数、神经元个数
减小正则化项的系数
添加正则化项是为了限制模型的学习能力，减小正则化项的系数则可以放宽这个限制
模型通常更倾向于更大的权重，更大的权重可以使模型更好的拟合数据

L1/L2 范数正则化

L1/L2 范数的作用、异同

相同点

限制模型的学习能力——通过限制参数的规模，使模型偏好于权值较小的目标函数，防止过拟合。

不同点

L1 正则化可以产生更稀疏的权值矩阵，可以用于特征选择，同时一定程度上防止过拟合；L2 正则化主要用于防止模型过拟合
L1 正则化适用于特征之间有关联的情况；L2 正则化适用于特征之间没有关联的情况。

为什么 L1 和 L2 正则化可以防止过拟合？

L1 & L2 正则化会使模型偏好于更小的权值。
更小的权值意味着更低的模型复杂度；添加 L1 & L2 正则化相当于为模型添加了某种先验，限制了参数的分布，从而降低了模型的复杂度。
模型的复杂度降低，意味着模型对于噪声与异常点的抗干扰性的能力增强，从而提高模型的泛化能力。——直观来说，就是对训练数据的拟合刚刚好，不会过分拟合训练数据（比如异常点，噪声）——奥卡姆剃刀原理

为什么 L1 正则化可以产生稀疏权值，而 L2 不会？

对目标函数添加范数正则化，训练时相当于在范数的约束下求目标函数 J 的最小值
带有L1 范数（左）和L2 范数（右）约束的二维图示

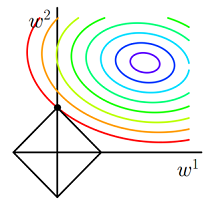
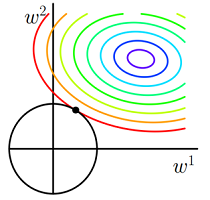
图中 J 与 L1 首次相交的点即是最优解。L1 在和每个坐标轴相交的地方都会有“顶点”出现，多维的情况下，这些顶点会更多；在顶点的位置就会产生稀疏的解。而 J 与这些“顶点”相交的机会远大于其他点，因此 L1 正则化会产生稀疏的解。
L2 不会产生“顶点”，因此 J 与 L2 相交的点具有稀疏性的概率就会变得非常小。

交叉验证的主要作用

为了得到更为稳健可靠的模型，使用验证集对模型的泛化误差进行评估，得到模型泛化误差的近似值。当有多个模型可以选择时，我们通常选择“泛化误差”最小的模型。

常用的交叉验证方法：留一交叉验证、k折交叉验证

$k$ 折交叉验证

$k$ 折交叉验证：将含有 $N$ 个样本的数据集，分成 $k$ 份，每份含有 $N/k$ 个样本。选择其中1份作为测试集，另外 $k-1$ 份作为训练集。这样就可以获得 $K$ 组训练/测试集，从而可以进行 $k$ 次训练和测试，最终返回这 $k$ 个测试结果的均值，做为模型最终的泛化误差。一般 $2 \leq k \leq 10$ ，$k$ 最常用的取值是 10，此时称为10折交叉验证：

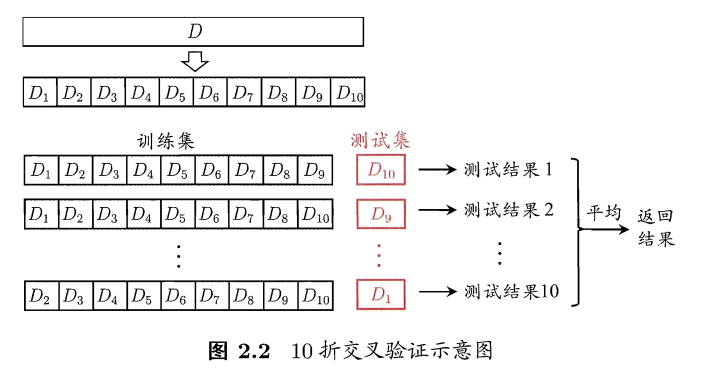
10次10折交叉验证： 则是如上重复做了10次，每次的10折交叉验证随机使用不同的划分。

训练集和测试集必须从完整的数据集中均匀取样。均匀取样的目的是希望减少训练集、测试集与原数据集之间的偏差。当样本数量足够多时，通过随机取样，便可以实现均匀取样的效果。

Precision和Recall

对于二分类问题，可将样例根据其真实类别与学习器预测类别的组合划分为：

TP (True Positive)：预测为真，实际为真
FP (False Positive)：预测为真，实际为假
TN (True Negative)：预测为假，实际为假
FN (False Negative)：预测为假，实际为真

令 TP、FP、TN、FN分别表示其对应的样例数，则显然有 TP + FP + TN + FN = 样例总数分类结果的 “混淆矩阵” 如下：

	实际为真 T	实际为假 F
预测为正例 P	TP (预测为1，实际为1)	FP (预测为1，实际为0)
预测为负例 N	FN (预测为0，实际为1)	TN (预测为0，实际为0)

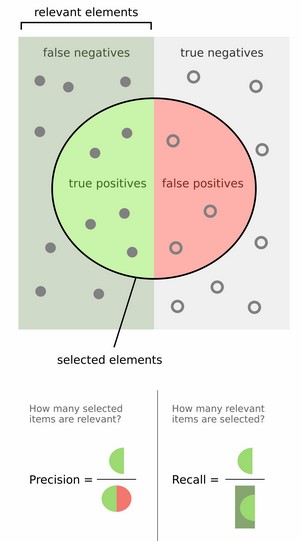
\[ （查准率）Precision = \frac{TP}{TP + FP} \\ \\ \\ {\color{Purple}{（预测的好瓜中有多少是真的好瓜）}} \]

\[ （查全率）Recall = \frac{TP}{TP + FN} \\ \\ {\color{Purple}{（所有真正的好瓜中有多少被真的挑出来了）}} \]

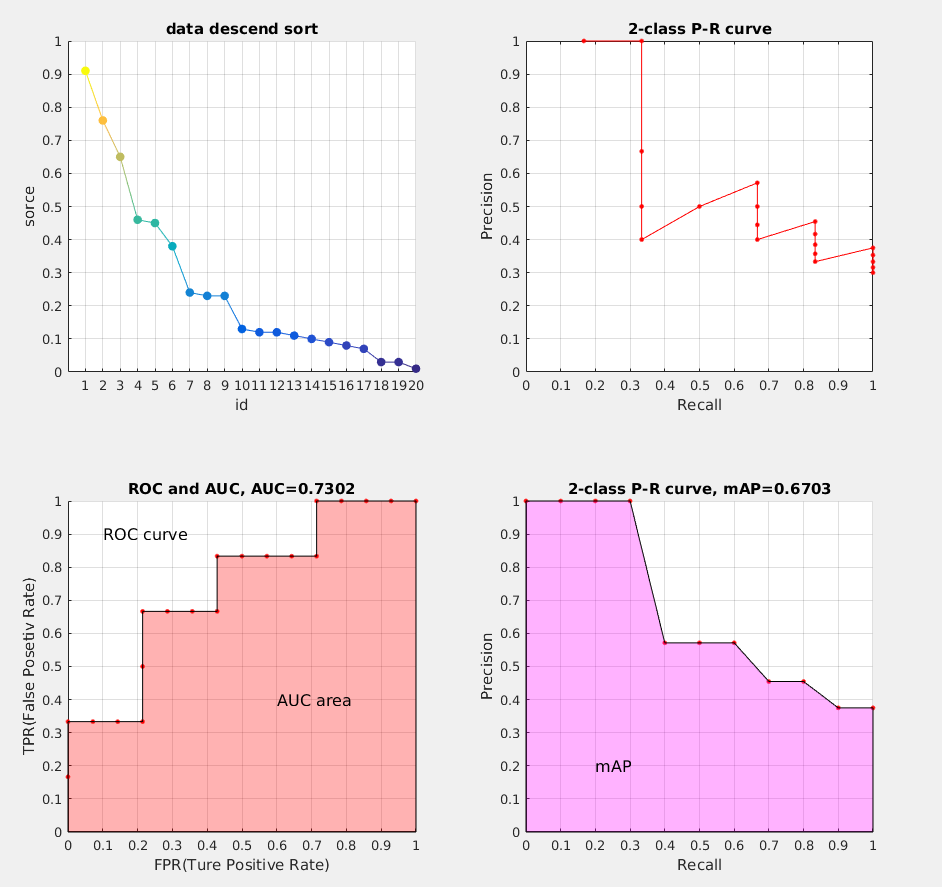
P-R曲线

一般来说，查准率高时，查全率往往偏低，而查全率高时，查准率往往偏低。通常只有在一些简单任务中，才可能使得查全率和查准率都很高。在很多情况，我们可以根据学习器的预测结果，得到对应预测的 confidence scores 得分(有多大的概率是正例)，按照得分对样例进行排序，排在前面的是学习器认为”最可能“是正例的样本，排在最后的则是学习器认为“最不可能”是正例的样本。每次选择当前第 $i$ 个样例的得分作为阈值 $(1 \leq i \leq 样例个数)$，计算当前预测的前 $i$ 为正例的查全率和查准率。然后以查全率为横坐标，查准率为纵坐标作图，就得到了我们的查准率-查全率曲线: P-R曲线

ROC与AUC

ROC 全称是“受试者工作特征”（Receiver Operating Characteristic）。ROC 曲线下的面积就是 AUC（Area Under the Curve）。AUC用于衡量“二分类问题”机器学习算法性能（泛化能力）。

思想：和计算 P-R 曲线方法基本一致，只是这里计算的是真正率(True Positive rate) 和假正率(False Positive rate)，以 FPR 为横轴，TPR 为纵轴，绘制的曲线就是 ROC 曲线，ROC 曲线下的面积，即为 AUC

\[ （真正率）TPR = \frac{TP}{TP + FN} \]

\[ （假正率）FPR = \frac{FP}{FP + TN} \]

mAP

接下来说说 AP 的计算，此处参考的是 PASCAL VOC CHALLENGE 的计算方法。首先按照 P-R曲线计算方式计算 Precision 和 Recall。然后设定一组阈值，[0, 0.1, 0.2, …, 1]，计算 Recall 大于第 $i$ 个阈值的R-P集合中，对应的 Precision 的最大值。这样，我们就计算出了11个 Precision。mAP 即为这11个 Precision 的平均值。这种方法英文叫做 11-point interpolated average precision
相应的Precision-Recall曲线（这条曲线是单调递减的）如下：

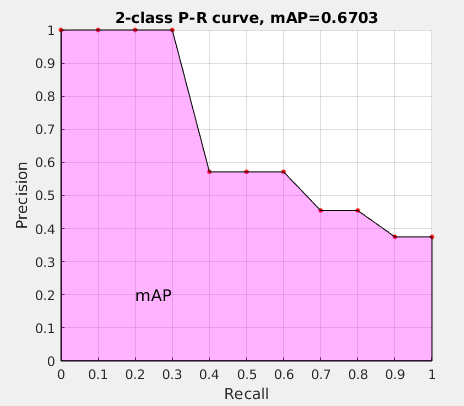
AP 衡量的是学出来的模型在每个类别上的好坏，mAP 衡量的是学出的模型在所有类别上的好坏，得到 AP 后 mAP 的计算就变得很简单了，就是取所有 AP 的平均值。

为什么要设置单一数字评估指标，设置指标的意义

在训练模型时，无论是调整超参数，还是调整不同的模型算法，我们都需要一个有效的评价指标，这个评价标准能帮助我们快速了解新的尝试后模型的性能是否更优。例如在分类时，我们通常会选择选择准确率，当样本不平衡时，查准率和查全率又会是更好的评价指标。所以在训练模型时，如果设置了单一数字的评估指标通常能很快的反应出我们模型的改进是否直接产生了收益，从而加速我们的算法改进过程。若在训练过程中，发现优化目标进一步深入，现有指标无法完全反应进一步的目标时，就需要重新选择评估指标了。

训练/验证/测试集的定义及划分

训练、验证、测试集在机器学习领域是非常重要的三个内容。三者共同组成了整个项目的性能的上限和走向。

训练集：用于模型训练的样本集合，样本占用量是最大的；
验证集：用于训练过程中的模型性能评价，跟着性能评价才能更好的调参；
测试集：用于最终模型的一次最终评价，直接反应了模型的性能。

在划分上，可以分两种情况：

1、在样本量有限的情况下，有时候会把验证集和测试集合并。实际中，若划分为三类，那么训练集：验证集：测试集=6:2:2；若是两类，则训练集：验证集=7:3。这里需要主要在数据量不够多的情况，验证集和测试集需要占的数据比例比较多，以充分了解模型的泛化性。

2、在海量样本的情况下，这种情况在目前深度学习中会比较常见。此时由于数据量巨大，我们不需要将过多的数据用于验证和测试集。例如拥有1百万样本时，我们按训练集：验证集：测试集=98:1:1的比例划分，1%的验证和1%的测试集都已经拥有了1万个样本。这已足够验证模型性能了。

此外，三个数据集的划分不是一次就可以的，若调试过程中发现，三者得到的性能评价差异很大时，可以重新划分以确定是数据集划分的问题导致还是由模型本身导致的。其次，若评价指标发生变化，而导致模型性能差异在三者上很大时，同样可重新划分确认排除数据问题，以方便进一步的优化。

什么是TOP5错误率

在很多情况，我们可以根据学习器的预测结果，得到对应预测的 confidence scores 得分(有多大的概率是正例)，按照得分对样例进行排序，取得分最高的前5个，计算这前5个都不是正例的概率，即为TOP5错误率。

如何通过模型重新观察数据

通过模型分析错误数据，推断是否存在错误标注或者漏标注等问题。此外，对于出现一些过拟合的情况，我们也可以通过观察来了解模型。例如分类任务，样本严重不平衡时，模型全预测到了一边时，其正确率仍然很高，但显然模型已经出现了问题。

有哪些改善模型的思路

改善模型本质是如何优化模型，这本身是个很宽泛的问题。也是目前学界一直探索的目的，而从目前常规的手段上来说，一般可取如下几点。

数据角度

增强数据集。无论是有监督还是无监督学习，数据永远是最重要的驱动力。更多的类型数据对良好的模型能带来更好的稳定性和对未知数据的可预见性。对模型来说，“看到过的总比没看到的更具有判别的信心”。但增大数据并不是盲目的，模型容限能力不高的情况下即使增大数据也对模型毫无意义。而从数据获取的成本角度，对现有数据进行有效的扩充也是个非常有效且实际的方式。良好的数据处理，常见的处理方式如数据缩放、归一化和标准化等。

模型角度

模型的容限能力决定着模型可优化的空间。在数据量充足的前提下，对同类型的模型，增大模型规模来提升容限无疑是最直接和有效的手段。但越大的参数模型优化也会越难，所以需要在合理的范围内对模型进行参数规模的修改。而不同类型的模型，在不同数据上的优化成本都可能不一样，所以在探索模型时需要尽可能挑选优化简单，训练效率更高的模型进行训练。

调参优化角度

如果你知道模型的性能为什么不再提高了，那已经向提升性能跨出了一大步。超参数调整本身是一个比较大的问题。一般可以包含模型初始化的配置，优化算法的选取、学习率的策略以及如何配置正则和损失函数等等。这里需要提出的是对于同一优化算法，相近参数规模的前提下，不同类型的模型总能表现出不同的性能。这实际上就是模型优化成本。从这个角度的反方向来考虑，同一模型也总能找到一种比较适合的优化算法。所以确定了模型后选择一个适合模型的优化算法也是非常重要的手段。

训练角度

很多时候我们会把优化和训练放一起。但这里我们分开来讲，主要是为了强调充分的训练。在越大规模的数据集或者模型上，诚然一个好的优化算法总能加速收敛。但你在未探索到模型的上限之前，永远不知道训练多久算训练完成。所以在改善模型上充分训练永远是最必要的过程。充分训练的含义不仅仅只是增大训练轮数。有效的学习率衰减和正则同样是充分训练中非常必要的手段。

激活函数

为什么需要激活函数？

激活函数对模型学习、理解非常复杂的、和非线性的函数具有重要作用
使用激活函数的目的是为了向网络中加入非线性因素 。从而加强网络的表示能力，解决线性模型无法解决的问题

为什么要使用非线性激活函数？

神经网络的万能近似定理认为，神经网络具有至少一个非线性隐藏层，那么只要给予网络足够数量的隐藏单元，它就可以以任意的精度来近似拟合任何从一个有限维空间到另一个有限维空间的函数。

如果不使用非线性激活函数，那么每一层输出都是上层输入的线性组合；此时无论网络有多少层，其整体也将是线性的，就做不到用非线性来逼近任意函数，导致失去万能近似的性质
使用非线性激活函数，可以增强网络的表示能力，使它可以学习从输入到输出之间复杂的非线性的映射。而且，仅部分层是纯线性是可以接受的，这有助于减少网络中的参数。

什么时候可以用线性激活函数

输出层，大多使用线性激活函数
在隐含层可能会使用一些线性激活函数
一般用到的线性激活函数很少

常见的激活函数

$Sigmoid$

$Sigmod$ 又叫作 $Logistic$ 激活函数，它将实数值压缩进 0 到 1 的区间内，还可以在预测概率的输出层中使用。该函数将大的负数转换成 0，将大的正数转换成 1
数学公式为：
\[ y = \sigma(x) = \frac{1}{1 + e^{-x}} \\ y' = y * (1 - y) \]
下图展示了 Sigmoid 函数及其导数：

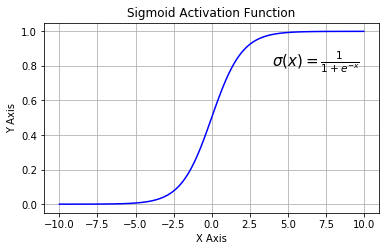
Sigmoid激活函数

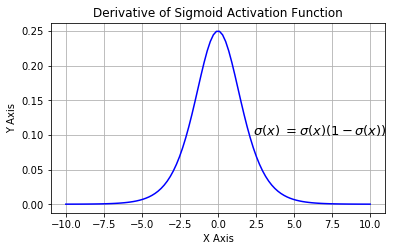
Sigmoid激活函数导数

$Sigmoid$ 函数的三个主要缺陷：
梯度消失：$Sigmoid$ 函数在输入取绝对值非常大的正值或负值时会出现饱和现象，在图像上表现为变得很平缓，此时函数会对输入的微小变化不敏感，即此时的梯度趋近于0，造成梯度消失，网络权重更新缓慢或不更新。
计算成本高昂：$exp()$ 函数与其他非线性激活函数相比，计算成本高昂
不以零为中心：Sigmoid 输出不以零为中心的

$Tanh$ 函数

\[ \tanh (x)=2 \sigma(2 x)-1=\frac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{\mathrm{e}^{x}+\mathrm{e}^{-x}} \\ \tanh ^{\prime}(x)=1-\tanh ^{2}(x) \]

$Tanh$ 函数又叫作双曲正切激活函数。与 $Sigmoid$ 函数类似，区别是值域为 $(-1, 1)$ ，且 $Tanh$ 函数的输出以零为中心，因为区间在 $-1$ 到 $1$ 之间。

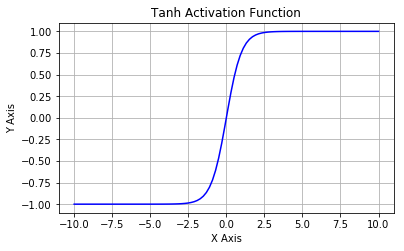
Tanh函数

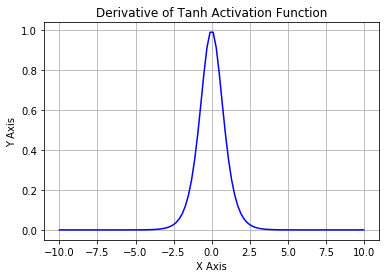
Tanh函数导数

缺点：
梯度消失： $Tanh$ 函数也会有梯度消失的问题，因此在饱和时也会「杀死」梯度。
计算成本高昂：$exp()$ 函数与其他非线性激活函数相比，计算成本高昂

为什么Tanh收敛速度比Sigmoid快

$tanh^{'}(x)=1-tanh(x)^{2}\in (0,1)$
$s^{'}(x)=s(x)*(1-s(x))\in (0,\frac{1}{4}]$

由上面两个公式可知 $Tanh$ 梯度消失的问题比 $Sigmoid$ 轻，所以 $Tanh$ 收敛速度比 $Sigmoid$ 快。

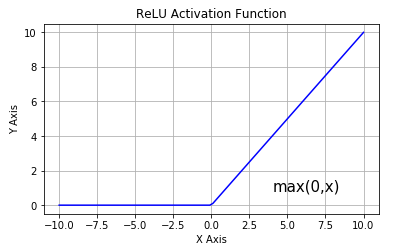
$Relu$ 函数

$ReLU$ 是从底部开始半修正的一种函数，数学公式为：
\[ f(x) = max(0, x) \]

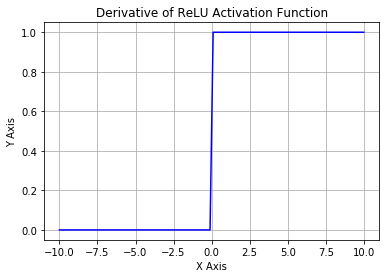
优点：
加速网络训练：当输入 $x < 0$ 时，输出为 0，当 $x > 0$ 时，输出为 $x$。该激活函数使网络更快速地收敛。
避免梯度消失： $ReLU$ 的导数始终是一个常数，负半区为 0，正半区为 1，所以不会发生梯度消失现象。而 $Sigmoid$ 函数在输入取绝对值非常大的正值或负值时会出现饱和现象.
减缓过拟合：$ReLU$ 在负半区的输出为 0。一旦神经元的激活值进入负半区，那么该激活值就不会产生梯度/不会被训练，造成了网络的稀疏性——稀疏激活 。这有助于减少参数的相互依赖，缓解过拟合问题的发生
加速计算：$ReLU$ 的求导不涉及浮点运算，所以速度更快
缺点：
不以零为中心：和 $Sigmoid$ 激活函数类似，$ReLU$ 函数的输出不以零为中心。
容易造成神经元死亡现象Dead ReLU Reference：比如对于一个神经元，当有一个比较大的梯度传递过来，导致该神经元的参数分布发生比较大的变化，变成一个低方差，中心在-0.1的高斯分布，这样以后，大部分数据输入该神经元之后为0，不能通过反向传播更新其参数，造成神经元死亡。这于是就引入了 $Leaky\ ReLU$ 来解决该问题。

$Leaky\ ReLU$

该函数试图缓解 dead ReLU 问题。数学公式为：
\[ f(x) = max(0.1x, x) \]

$Leaky\ ReLU$ 的概念是：当 $x < 0$ 时，它得到 0.1 的正梯度。该函数一定程度上缓解了 dead ReLU 问题，但是使用该函数的结果并不连贯。尽管它具备 $ReLU$ 激活函数的所有特征，如计算高效、快速收敛、在正区域内不会饱和。

$Leaky\ ReLU$ 可以得到更多扩展。不让 $x$ 乘常数项，而是让 $x$ 乘超参数，这看起来比 $Leaky\ ReLU$ 效果要好。该扩展就是 $Parametric\ ReLU$。

$Parametric\ ReLU$

\[ f(x) = max(ax, x) \]

其中 $\alpha$ 是一个可以学习的参数，因为你可以对它进行反向传播。这使神经元能够选择负区域最好的梯度，有了这种能力，它们可以变成 ReLU 或 Leaky ReLU。

怎样理解 ReLU（< 0 时）是非线性激活函数

从 $ReLU$ 的图像可以看出具有一下特点：

单侧抑制
相对宽阔的兴奋边界
稀疏激活性

$ReLU$ 函数从图像上看，是一个分段线性函数，把所有的负值都变为 0，而正值不变，这样就成为单侧抑制。因为有了这单侧抑制，才使得神经网络中的神经元也具有了稀疏激活性。

损失函数/代价函数

损失函数 $| y_i-f(x_i)|$ ，一般是针对单个样本 $i$

代价函数 $\frac{1}{N}\sum_{i=1}^{N}{| y_i-f(x_i)}|$ ，一般是针对总体$N$

目标函数 $\frac{1}{N}\sum_{i=1}^{N}{| y_i-f(x_i)}| + 正则化项$

(其实 损失函数 和 代价函数 可以理解成同一个东西)

损失函数（loss function）是用来估量模型的预测值 $f(X)$ 与真实值 $Y$ 的不一致程度，它是一个非负实值函数，通常使用 $L(Y, f(X))$ 来表示，损失函数越小，模型的鲁棒性就越好。训练数据集的平均损失称为经验风险 。结构风险最小化 是为了防止过拟合而提出来的策略，结构风险在经验风险基础上加上正则化项(regularizer)或惩罚项(penalty term)，[李航P8] 通常可以表示为如下形式：
\[ \theta^{*}=\arg \min _{\theta} \frac{1}{N} \sum_{i=1}^{N} L\left(y_{i}, f\left(x_{i} ; \theta\right)\right)+\lambda \Phi(\theta) \]
其中，前面的均值函数表示的是经验风险函数，$L$ 代表的是损失函数，后面的 $Φ$ 是正则化项，它可以是 $L1$，也可以是 $L2$，或者其他的正则函数。整个式子表示的意思是找到使目标函数最小时的 $θ$ 值。

为什么需要损失/代价函数

用于找到最优解的目标/假设函数（用于衡量假设函数的准确性）比如：为了得到逻辑回归模型的参数，需要一个代价函数，通过训练代价函数来得到参数。

损失/代价函数的作用及原理

使用线性回归的例子说明，用一条直线，拟合给定的数据，使用均方误差损失函数，梯度下降法来拟合。

为什么损失/代价函数要非负

目标函数存在一个下界，在优化过程当中，如果优化算法能够使目标函数不断减小，根据单调有界准则，这个优化算法就能证明是收敛有效的。只要设计的目标函数有下界，基本上都可以，代价函数非负更为方便。

常用的损失函数

（1）0-1 损失函数

如果预测值 $f(X)$ 和目标值 $Y$ 相等，值为 0，如果不相等，值为 1：
\[ L(Y, f(X)) = \begin{cases} 1,& Y\ne f(X)\\ 0,& Y = f(X) \end{cases} \]
一般的在实际使用中，相等的条件过于严格，可适当放宽条件：
\[ L(Y, f(X)) = \begin{cases} 1,& |Y-f(X)|\geqslant T\\ 0,& |Y-f(X)|< T \end{cases} \]
（2）绝对值损失函数（L1 Loss、LAE）

L1范数损失函数，也称作最小绝对值偏差( least absolute deviations, LAD)，最小绝对值误差(least absolute errors, LAE)。目的是将估计值 $f(X)$ 和目标值 $Y$ 的绝对差值的总和 $L$ 最小化：
\[ L(Y, f(X)) = |Y-f(X)| \\ \color{green}{（此时的 \ X \ 是只有一个样本的输入）} \]
在实际应用中，$X$ 样本个数为 $m$ ，通常会使用 平均最小绝对值误差 (MAE) 做为 L1 Loss 形式：
\[ L(Y, f(X)) = \frac{1}{m}\sum_{i=1}^m|Y-f(X)| \\ \color{green}{（此时的 \ X \ 有 \ m \ 个样本的输入）} \]
（3）平方损失函数 (L2 Loss、LSE、最小二乘法OLS)

基于均方误差最小化(平方损失函数)来进行模型求解的方法称为: $\mathbf{\color{green}{最小二乘法}}$. 在线性回归中，最小二乘法就是试图找到一条直线，使得所有样本到直线上的欧氏距离之和最小. (其假设样本和噪声都服从$\mathbf{\color{blue}{高斯分布}}$，然后通过极大似然估计(MLE)可以推导出最小二乘式子)
即 OLS 是基于距离的，而这个距离就是我们用的最多的欧几里得距离。为什么它会选择使用欧式距离作为误差度量呢？ (即Mean squared error， MSE)，主要有以下几个原因：

简单，计算方便

欧氏距离是一种很好的相似性度量标准

在不同的表示域变换后特征性质不变

平方损失（Square loss）的标准形式如下：

\[ L(Y,f(X))=(Y-f(X))^2. \]
- 当样本个数为 $m$ 时，此时损失函数变为：

\[ L(Y, f(X)) = \sum_{i = 1}^{m}(Y - f(X)) \]

$Y-f(X)$ 表示的是残差，整个式子表示的是 残差的平方和，而我们的目的就是最小化这个目标函数值 (注：该式子未加入正则项)，也就是最小化残差的平方和（residual sum of squares, RSS）
而在实际应用中，通常会使用 均方误差 (MSE) 作为一项衡量指标，公式如下：
\[ MSE = \frac{1}{m}\sum_{i = 1}^{m}(Y - f(X))^2 \]
> 最常用的是平方损失，然而其缺点是对于异常点会施以较大的惩罚，因而不够robust。如果有较多异常点，则绝对值损失表现较好，但绝对值损失的缺点是在 $y-f(x)=0$ 处不连续可导，因而不容易优化。

（4）对数损失函数（逻辑回归）
\[ L(Y,P(Y|X))=-logP(Y|X). \]
常见的逻辑回归使用的就是对数损失函数，而不是平方损失。逻辑回归它假设样本服从 $\mathbf{\color{blue}{伯努利分布（0-1分布）}}$，进而求得满足该分布的似然函数，接着取对数求极值等。而逻辑回归并没有求似然函数的极值，而是把极大化当做是一种思想，进而推导出它的经验风险函数为：最小化负的似然函数，从损失函数的角度看，就是 $log$ 损失函数。

损失函数 $L(Y, P(Y|X))$ 表达的是样本 $X$ 在分类 $Y$ 的情况下，使概率 $P(Y|X)$ 达到最大值（换言之，就是利用已知的样本分布，找到最有可能（即最大概率）导致这种分布的参数值；或者说什么样的参数才能使我们观测到目前这组数据的概率最大）因为 $log$ 函数是单调递增的，所以 $logP(Y|X)$ 也会达到最大值，因此在前面加上负号之后，最大化 $P(Y|X)$ 就等价于最小化 $L$ 了。

逻辑回归 的 $P(Y=y|x)$ 表达式如下（为了将类别标签 $y$ 统一为1和0，下面将表达式分开表示）：
\[ P(Y=y | x)=\left\{\begin{array}{cc}{h_{\theta}(x)=g(f(x))=\frac{1}{1+\exp (-f(x)\}}} & {, y=1} \\ {1-h_{\theta}(x)=1-g(f(x))=\frac{1}{1+\exp (f(x)\}}} & {, y=0}\end{array}\right. \]
将它带入到上式，通过推导可以得到logistic的损失函数表达式，如下：
\[ L(y, P(Y=y | x))=\left\{\begin{array}{cc}{\log (1+\exp \{-f(x)\})} & {, y=1} \\ {\log (1+\exp \{f(x)\})} & {, y=0}\end{array}\right. \]
逻辑回归最后得到的目标式子如下：
\[ J(\theta)=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right] \]
（5）指数损失函数

指数损失函数的标准形式为：
\[ L(y|f(x))=exp[-yf(x)]. \]
例如 AdaBoost 就是以指数损失函数为损失函数。

（6）Hinge 损失函数

Hinge 损失函数的标准形式如下：
\[ L(y)=max(0, 1-ty). \]
其中 $y$ 是预测值，范围为 $(-1,1), $ $t$ 为目标值，其为 $-1 或 1$。
在线性支持向量机中，最优化问题可等价于：
\[ \underset{w,b}{min}\sum_{i=1}^{N}(1-y_i(wx_i+b))+\lambda \lVert w^2 \rVert \]

\[ \frac{1}{m}\sum_{i=1}^{N}l(wx_i+by_i))+\lVert w^2 \rVert \]

其中 $l(wx_i+by_i))$ 是Hinge损失函数，$\lVert w^2 \rVert$ 可看做为正则化项。

Reference: 机器学习-损失函数

Softmax损失函数

Softmax 函数 $\sigma(z)=\left({\color{Red}{\sigma_{1}(z)}}, \ldots, \sigma_{m}(z)\right)$ 定义如下：
\[ {\color{Green}{o_i}} = {\color{Red}{\sigma_{i}(z)}} =\frac{\exp \left(z_{i}\right)}{\sum_{j=1}^{m} \exp \left(z_{j}\right)}, \quad i=1, \ldots, m \\ {\color{Green}{\small{【观察到的数据 \ x \ (或z)\ 属于类别\ i\ 的概率，或者称作似然 (Likelihood)】}}} \]
它在 Logistic Regression 里其到的作用是将线性预测值转化为类别概率：$m$ 代表类别数，假设 $z_{i}=\theta_{i}^{T} x$ 是第 $i$ 个类别的线性预测结果，带入 $Softmax$ 的结果其实就是先对每一个 $z_i$ 取 exponential 变成非负，然后除以所有项之和进行归一化，现在每个 $o_{i}=\sigma_{i}(z)$ 就可以解释成：观察到的数据 $x$ 属于类别 $i$ 的概率，或者称作似然 (Likelihood)。

然后 Logistic Regression 的目标函数是根据最大似然原则来建立的，假设数据 $x$ 所对应的类别为 $y$，则根据我们刚才的计算最大似然就是要最大化 $o_y$ 的值 (通常是使用 negative log-likelihood 而不是 likelihood，也就是说最小化 $-log(o_y)$ 的值，这两者结果在数学上是等价的)。后面这个操作就是 caffe 文档里说的 Multinomial Logistic Loss，具体写出来是这个样子：
\[ \ell(y, o)=-\log \left(o_{y}\right) \]
Softmax 函数梯度计算

Softmax层 输出为 $o_i = \sigma_i(z)$ ，其对输入 $z_k$ 的梯度为:
\[ \begin{aligned} \frac{\partial o_{i}}{\partial z_{k}} & = \frac{\partial}{\partial z_{k}} \frac{\exp \left(z_{i}\right)}{\sum_{j=1}^{m} \exp \left(z_{j}\right)} \\ & =\frac{\delta_{i k} e^{z_{i}}\left(\sum_{j=1}^{m} e^{z_{j}}\right)-e^{z_{i}} e^{z_{k}}}{\left(\sum_{j=1}^{m} e^{z_{j}}\right)^{2}} \\ & =\delta_{i k} o_{i}-o_{i} o_{k} \end{aligned} \]
即 Softmax 层的梯度为：
\[ \begin{aligned} \frac{\partial o_{i}}{\partial z_{k}} = \begin{cases} o_i(1 - o_k), & k = i \\ - o_i o_k, & k \ne i \end{cases} \end{aligned} \]

Softmax-Loss损失函数

而 Softmax-Loss 其实就是把两者结合到一起，只要把 $o_y$ 的定义展开即可：
\[ \tilde{\ell}(y, z)=-\log \left(\frac{e^{z_{y}}}{\sum_{j=1}^{m} e^{z_{j}}}\right)=\log \left(\sum_{j=1}^{m} e^{z_{j}}\right)-z_{y} \\ {\color{Green}{\small{【将观察到的数据 \ x \ (或z)\ 属于类别 \ y \ 的概率做最大似然估计，或最小\ negative\ log\ 似然】}}} \]
梯度计算：

计算输入数据 $z_k$ 属于类别 $y$ 的概率的极大似然估计。由于 Softmax-Loss 层是最顶层的输出层，则可以直接用最终输出 (loss): $\tilde{\ell}(y, z)$ 求对输入 $z_k$ 的偏导数：
\[ \begin{aligned} \frac{\partial \tilde{\ell}(y, z)}{\partial z_{k}} & = \frac{\partial}{\partial z_{k}} \left(\log \left(\sum_{j=1}^{m} e^{z_{j}}\right)-z_{y} \right)\\ & = \frac{\exp \left(z_{k}\right)}{\sum_{j=1}^{m} \exp \left(z_{j}\right)}-\delta_{k y}=\sigma_{k}(z)-\delta_{k y} \end{aligned} \]
其中 $\sigma_k(z)$ 是 Softmax-Loss 的中间步骤 Softmax 在 Forward Pass 的计算结果，而
\[ \delta_{k y}=\left\{\begin{array}{ll}{1} & {k=y} \\ {0} & {k \neq y}\end{array}\right. \]
即 Softmax-Loss 层的梯度为：
\[ \begin{aligned} \frac{\partial \tilde{\ell}(y, z)}{\partial z_{k}} = \begin{cases} \sigma_{k}(z) - 1 , & k = y \\ \sigma_{k}(z) , &k \ne y \end{cases} \end{aligned} \]

熵、条件熵、KL散度、交叉熵

信息论背后的原理是：从不太可能发生的事件中能学到更多的有用信息。

发生可能性较大的事件包含较少的信息。

发生可能性较小的事件包含较多的信息。

独立事件包含额外的信息。

【通俗理解】

熵：可以表示一个事件A的自信息量，也就是A包含多少信息（表示随机变量不确定性的度量，所有可能发生的事件产生的信息量的期望）

KL散度：可以用来表示从事件B的角度来看，事件A有多大不同

交叉熵：可以用来表示从事件B的角度来看，如何描述事件A

条件熵： H(Y|X) 表示已知随机变量X的条件下，随机变量Y的不确定性

【概括】：KL散度可以被用于计算代价，而在特定情况下最小化KL散度等价于最小化交叉熵。而交叉熵的运算更简单，所以用交叉熵来当做代价

熵(entropy)： 在信息论中表示一个事件所包含的信息量，所有可能发生事件产生的信息量的期望 (对A时间中的随机变量进行编码所需要的最小字节数)

越不可能发生的事件信息量越大，比如“我不会死”这句话信息量就很大。而确定事件的信息量就很低，比如“我是我妈生的”，信息量就很低甚至为0
独立事件的信息量可叠加。比如“a. 张三今天喝了阿萨姆红茶，b. 李四前天喝了英式早茶”的信息量就应该恰好等于a+b的信息量，如果张三李四喝什么茶是两个独立事件。

自信息：对于事件 $X = x$ ，定义自信息 self-information 为： $I(x) = -logP(x)$ 自信息仅仅处理单个输出，但是如果计算自信息的期望，它就是熵.

熵的定义：
\[ S(x)=-\sum_{i= 1}^{n} P\left(x_{i}\right) \log P\left(x_{i}\right) \]
$x$ 指不同的事件，比如喝茶。$P(x_i)$ 指的是某个事件发生的概率，比如喝红茶的概率。对于一个一定会发生的事件，其发生概率为1，$S(x)=-\log (1) * 1=-0 * 1=0$ ，信息量为0.

KL散度/相对熵(Kullback-Leibler Divergence)： 衡量两个事件(分布)之间的差异 (刻画了非真实分布B编码真实分布A带来的平均编码长度的增量)

对于给定的随机变量 $X$，它的两个单独的概率分布函数 $A(X) 和 B(X)$ 的区别，可以用 KL 散度来度量。KL散度，有时候也叫KL距离，一般被用于计算两个分布之间的差异。看名字似乎跟计算两个点之间的距离也很像，但实则不然，因为KL散度不具备有对称性。在距离上的对称性指的是A到B的距离等于B到A的距离。

KL散度的数学定义：

对于离散事件我们可以定义事件A和B的差别为(2.1)：

\[ D_{K L}(A \| B)=\sum_{i} P_{A}\left(x_{i}\right) \log \left(\frac{P_{A}\left(x_{i}\right)}{P_{B}\left(x_{i}\right)}\right)=\sum_{i} P_{A}\left(x_{i}\right) \log \left(P_{A}\left(x_{i}\right)\right)-P_{A}\left(x_{i}\right) \log \left(P_{B}\left(x_{i}\right)\right) \\ {\color{blue}{事件 A 与 B之间的对数差 \ 在 A上的期望}} \]

对于连续事件，那么我们只是把求和改为求积分而已(2.2)：

\[ D_{K L}(A \| B)=\int a(x) \log \left(\frac{a(x)}{b(x)}\right) \]

从公式中可以看出：

如果 $P_A=P_B$ ，即两个事件/分布完全相同，那么KL散度等于0
其中 $-\sum_{i} P_{A}\left(x_{i}\right) \log \left(P_{A}\left(x_{i}\right)\right)$ 就是事件A的熵
如果颠倒一下顺序求 $D_{KL}(B||A)$ ，那么就需要使用B的熵，答案就不一样了。所以KL散度来计算两个分布A与B的时候是不是对称的，有“坐标系”的问题，$D_{K L}(A \| B) \neq D_{K L}(B \| A)$

换句话说，KL散度由A自己的熵与B在A上的期望共同决定。当使用KL散度来衡量两个事件(连续或离散)，上面的公式意义就是求 A与B之间的对数差在 A上的期望值。

交叉熵(cross entropy) = KL散度 + 熵 描述两个事件之间的相互关系 (刻画了用非真实分布B来表示真实分布A中的样本的平均编码长度)

如果我们默认了用KL散度来计算两个分布间的不同，那还要交叉熵做什么？

事实上交叉熵和KL散度的公式非常相近，其实就是KL散度的后半部分(公式2.1)：A和B的交叉熵 = A与B的KL散度 + A的熵。$D_{K L}(A \| B)=-S(A)+H(A, B)$

KL散度的公式

熵的公式

\[ S(A)=-\sum_{i} P_{A}\left(x_{i}\right) \log P_{A}\left(x_{i}\right) \]

交叉熵公式

\[ H(A, B)=-\sum_{i} P_{A}\left(x_{i}\right) \log \left(P_{B}\left(x_{i}\right)\right) \]

如果 $S(A)$ 是一个常量，那么 $D_{KL}(A||B) = H(A,B)$ ，也就是说KL散度和交叉熵在特定条件下等价。 比如我们的A为真实分布，B为非真实分布，即KL散度前者是真实分布的熵，后者是交叉熵，由于真实分布是固定的，所以信息熵的值是固定的。此时的KL散度和交叉熵是等价的。

交叉熵性质
- 和KL散度相同，交叉熵也不具备对称性：$H(A, B) \neq H(B, A)$
- 从名字上来看，Cross(交叉)主要是用于描述两个事件之间的相互关系，对自己求交叉熵等于熵。即 $H(A, A)=S(A)$ ，注意只是非负而不一定等于0。
交叉熵和KL散度的联系
- 不同之处：交叉熵中不包括“熵”的部分
- 相同之处：a. 都不具备对称性 b. 都是非负的
- 等价条件：当 A 固定不变时，那么最小化KL散度 $D_{KL}(A||B) $ 等价于最小化交叉熵 $H(A,B)$ 。$D_{KL}(A||B) = H(A,B)$

条件熵(conditional entropy)： H(Y|X):表示已知随机变量X的条件下，随机变量Y的不确定性.

条件熵的公式
实例理解

\[ \begin{aligned} H(Y | X) &=\sum_{x \in X} p(x) H(Y | X=x) \\ &=-\sum_{x \in X} p(x) \sum_{y \in Y} p(y | x) \log p(y | x) \\ &=-\sum_{x \in X} \sum_{y \in Y} p(x, y) \log p(y | x) \end{aligned} \]

总结
- 其实条件熵意思是按一个新的变量的每个值对原变量进行分类，(比如上面这个题把嫁与不嫁按帅，不帅分成了俩类) 然后在每一个小类里面，都计算一个小熵，然后每一个小熵乘以各个类别的概率，然后求和。
- 我们用另一个变量对原变量分类后，原变量的不确定性就会减小了，因为新增了X的信息，可以感受一下。不确定程度减少了多少就是信息的增益。
性质

\[ H(X, Y)=H(Y | X)+H(X) \\ 即：描述 X 和 Y 所需要的信息是：描述 X 所需要的信息加上给定 X 条件下描述 Y 所需的额外信息。 \]

机器如何“学习”

在机器学习中，我们希望在训练数据上模型学到的分布 $P(model)$ 和真实数据的分布 $P(real)$ 越接近越好，所以我们可以使其相对熵最小。但是我们没有真实数据的分布，所以只能希望模型学到的分布 $P(model)$ 和训练数据的分布 $P(train)$ 尽量相同。假设训练数据是从总体中独立同分布采样的，那么我们可以通过最小化训练数据的经验误差来降低模型的泛化误差。即：

希望学到的模型的分布和真实分布一致，$P(model)≃P(real)$
但是真实分布不可知，假设训练数据是从真实数据中独立同分布采样的，$P(train)≃P(real)$
因此，我们希望学到的模型分布至少和训练数据的分布一致，$P(train)≃P(model)$

由此非常理想化的看法是如果模型(左)能够学到训练数据(中)的分布，那么应该近似的学到了真数据(右)的分布：$P(model)≃P(train)≃P(real)$

为什么交叉熵可以用作代价？

最小化模型分布 $P(model)$ 与训练数据上的分布 $P(train)$ 的差异，等价于最小化这两个分布间的KL散度，也就是最小化 $D_{KL}(P(train)||P(model))$

对比上面的KL散度公式

A就是数据的真实分布：$P(train)$
B就是模型从训练数据上学到的分布：$P(model)$

而训练数据的分布A是给定的，是固定的，即A的信息熵是固定的，此时求 $D_KL(A||B)$ 等价于求 $H(A, B)$ ，也就是 A 与 B 的交叉熵。得证，交叉熵可以用于计算“学习模型的分布”与“训练数据分布”之间的不同。当交叉熵最低时(等于训练数据分布的熵)，我们学到了“最好的模型”。

Reference: 参考一参考二参考三参考四参考五

为什么用交叉熵代替二次代价(均方误差)函数

二次代价函数（quadratic cost）

当使用 sigmoid 函数作为激活函数：$\sigma(z)=\frac{1}{1+e^{-z}}$ ，此时的二次代价函数为
\[ J(\theta) = \frac{1}{2m}\sum_{i = 1}^{m}(h(x^{(i)} - y^{(i)})^2) \]
假如使用梯度下降法（Gradient descent）来调整权值的参数大小，为了说明方便，我们用单个样本为例，此时二次代价函数为：
\[ J = \frac{(a - y)^2}{2} \]
a = σ(z) 表示该神经元的输入，$y$ 表示真实值，参数调整需要求损失函数的偏导：
\[ \begin{aligned} \frac{\partial J}{\partial w} &=(a-y) \sigma^{\prime}(z) x \\ \frac{\partial J}{\partial b} &=(a-y) \sigma^{\prime}(z) \end{aligned} \]
参数沿着梯度方向调整参数大小，不足的地方在于，当初始的误差越大，收敛得越缓慢 (sigmoid输入绝对值非常大的值，是饱和区域，梯度很小 Reference)

交叉熵代价函数（cross-entropy）
\[ J = -\frac{1}{n}\sum_x[y\ln a + (1-y)\ln{(1-a)}] \]

其中, a = σ(z)最终求导得到更新权重时的偏导:
\[ \begin{aligned} \frac{\partial J}{\partial w} &=\frac{1}{n} \sum_{x}(\sigma(z)-y) x_{j} \\ \frac{\partial J}{\partial b} &=\frac{1}{n} \sum_{x}(\sigma(z)-y) \end{aligned} \]
当误差越大时，梯度就越大，权值 $w$ 和偏置 $b$ 调整就越快，训练的速度也就越快，从而达到更快收敛的目。

范数

什么是范数？

我们知道距离的定义是一个宽泛的概念，只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化了的距离概念，它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解，我们可以把范数当作距离来理解。

在数学上，范数包括 向量范数 和 矩阵范数，向量范数表征向量空间中向量的大小，矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是，对应向量范数，向量空间中的向量都是有大小的，这个大小如何度量，就是用范数来度量的，不同的范数都可以来度量这个大小，就好比米和尺都可以来度量远近一样；对于矩阵范数，学过线性代数，我们知道，通过运算 $AX=B$，可以将向量 $X$ 变化为 $B$，矩阵范数就是来度量这个变化大小的。这里简单地介绍以下几种向量范数的定义和含义

L-P范数

与闵可夫斯基距离的定义一样，L-P范数不是一个范数，而是一组范数，其定义如下：
\[ Lp=\sqrt[p]{\sum\limits_{i = 1}^n x_i^p}，x=(x_1,x_2,\cdots,x_n) \]
根据 $p$ 的变化，范数也有着不同的变化，一个经典的有关 $p$ 范数的变化图如下：

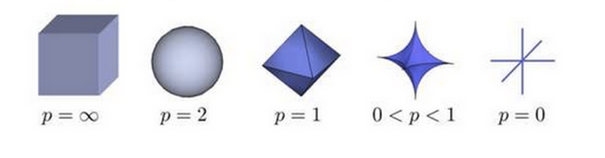
上图表示了 $p$ 从无穷到0变化时，三维空间中到原点的距离（范数）为1的点构成的图形的变化情况。以常见的 L-2范数(p=2)为例，此时的范数也即欧氏距离，空间中到原点的欧氏距离为1的点构成了一个球面。
实际上，在 $0≤p<1$ 时，$L_p$ 并不满足三角不等式的性质，也就不是严格意义下的范数。以$p=0.5$ ，二维坐标 $(1,4)、(4,1)、(1,9)$ 为例，$\sqrt[0.5]{(1+\sqrt{4})}+\sqrt[0.5]{(\sqrt{4}+1)}<\sqrt[0.5]{(1+\sqrt{9})}$ ，因此这里的 L-P 范数只是一个概念上的宽泛说法。

L0范数

当 $p=0$ 时，也就是 L0 范数，由上面可知，L0范数并不是一个真正的范数，它主要被用来度量向量中非零元素的个数。用上面的L-P定义可以得到的L-0的定义为：
\[ ||x||_{0}=\sqrt[0]{\sum\limits_1^nx_i^0}，x=(x_1,x_2,\cdots,x_n) \]
这里就有点问题了，我们知道非零元素的零次方为1，但零的零次方，非零数开零次方都是什么鬼，很不好说明 L0 的意义，所以在通常情况下，大家都用的是：

$||x_0||$ = # $( i|x_i\neq 0)$

表示向量 $x$ 中非零元素的个数。

对于L0范数，其优化问题为：
\[ min||x||_0 \\ s.t. Ax=b \]
在实际应用中，由于 L0 范数本身不容易有一个好的数学表示形式，给出上面问题的形式化表示是一个很难的问题，故被人认为是一个NP难问题。所以在实际情况中，L0的最优问题会被放宽到 L1 或 L2 下的最优化。

L1范数

L1范数是我们经常见到的一种范数，它的定义如下：
\[ ||x||_1=\sum_i|x_i| \]

表示向量 $x$ 中非零元素的绝对值之和

L1范数有很多的名字，例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异，如绝对误差和（Sum of Absolute Difference）：
\[ SAD(x_1,x_2)=\sum_i|x_{1i}-x_{2i}| \]
对于 L1 范数，它的优化问题如下：
\[ min||x||_1 \\ s.t.Ax=b \]
由于 L1 范数的天然性质，对 L1 优化的解是一个稀疏解，因此 L1范数也被叫做稀疏规则算子。通过L1 可以实现特征的稀疏，去掉一些没有信息的特征，例如在对用户的电影爱好做分类的时候，用户有100个特征，可能只有十几个特征是对分类有用的，大部分特征如身高体重等可能都是无用的，利用 L1 范数就可以过滤掉。

L2范数

L2范数是我们最常见最常用的范数了，我们用的最多的度量距离欧氏距离就是一种 L2 范数，它的定义如下：
\[ ||x||_2=\sqrt{\sum_ix_i^2} \]

表示向量元素的平方和再开平方

像 L1 范数一样，L2 也可以度量两个向量间的差异，如平方差和（Sum of Squared Difference）:
\[ SSD(x_1,x_2)=\sum_i(x_{1i}-x_{2i})^2 \]
对于L2范数，它的优化问题如下：
\[ min||x||_2 \\ s.t.Ax=b \]
L2 范数通常会被用来做优化目标函数的正则化项，防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力。

L-∞范数

当 $P=∞$ 时，也就是 $L∞$ 范数，它主要被用来度量向量元素的最大值。用上面的 L-P 定义可以得到的 $L∞$ 的定义为：
\[ ||x||_\infty=\sqrt[\infty]{\sum\limits_1^nx_i^\infty}，x=(x_1,x_2,\cdots,x_n) \]
与 L0 一样，在通常情况下，大家都用的是：
\[ ||x||_\infty=max(|x_i|) \]
来表示 $L∞$

欧式距离与余弦相似度

区别

假设 2人对三部电影的评分分别是 A = [3, 3, 3] 和 B = [5, 5, 5]
那么2人的欧式距离是 $\sqrt{12} = 3.46$， A、B的余弦相似度是1（方向完全一致）

余弦值的范围是[-1, 1], 越接近于1，说明2个向量的方向越相近

欧式距离和余弦相似度都能度量2个向量之间的相似度，但是欧式距离从2点之间的距离去考量，余弦相似从2个向量之间的夹角去考量。从上例可以发出，2人对三部电影的评价趋势是一致的，但是欧式距离并不能反映出这一点，余弦相似则能够很好地反应。余弦相似可以很好地规避指标刻度的差异，最常见的应用是计算 文本的相似度 。

联系

（1）欧式距离和余弦相似度都能度量 2 个向量之间的相似度

（2）放到向量空间中看，欧式距离衡量两点之间的直线距离，而余弦相似度计算的是两个向量之间的夹角

（3）没有归一化时，欧式距离的范围是 [0, +∞]，而余弦相似度的范围是 [-1, 1]；余弦距离是计算相似程度，而欧氏距离计算的是相同程度（对应值的相同程度）

（4）归一化的情况下，可以将空间想象成一个超球面（三维），欧氏距离就是球面上两点的直线距离，而向量余弦值等价于两点的球面距离，本质是一样。

例题解释

假设二维空间两个点： $A(x_1, y_1),\ B(x_2,y_2)$

欧氏距离（Euclidean Distance）

\[ euc = \sqrt{(x_1 - y_1)^2 + (x_2-y_2)^2} \]

余弦定义

\[ \cos (\theta)=\frac{<A, B>}{|A||B|} \ \ \ \ (分子为乡里的内积) \]

然后归一化为单位向量， $A\left(\frac{x_{1}}{\sqrt{x_{1}^{2}+y_{1}^{2}}}, \frac{y_{1}}{\sqrt{x_{1}^{2}+y_{1}^{2}}}\right), B\left(\frac{x_{2}}{\sqrt{x_{2}^{2}+y_{2}^{2}}}, \frac{y_{2}}{\sqrt{x_{2}^{2}+y_{2}^{2}}}\right)$

余弦相似度为：$\cos =\frac{x_{1}}{\sqrt{x_{1}^{2}+y_{1}^{2}}} \times \frac{x_{2}}{\sqrt{x_{2}^{2}+y_{2}^{2}}}+\frac{y_{1}}{\sqrt{x_{1}^{2}+y_{1}^{2}}} \times \frac{y_{2}}{\sqrt{x_{2}^{2}+y_{2}^{2}}}，(分母是1省略了)$

欧式距离为：$e u c=\sqrt{\left(\frac{x_{1}}{\sqrt{x_{1}^{2}+y_{1}^{2}}}-\frac{x_{2}}{\sqrt{x_{2}^{2}+y_{2}^{2}}}\right)^{2}+\left(\frac{y_{1}}{\sqrt{x_{1}^{2}+y_{1}^{2}}}-\frac{y_{2}}{\sqrt{x_{2}^{2}+y_{2}^{2}}}\right)^{2}}$

简化后就是：$e u c=\sqrt{2-2 \times \cos }$ ，即化简后计算的欧式距离是关于余弦相似度的单调函数，可以认为归一化后，余弦相似与欧式距离效果是一致的（欧式距离越小等价于余弦相似度越大）

因此可以将 求余弦相似转为求欧式距离 ，余弦相似的计算复杂度过高（需要两两比较 $O(n^2)$），转为求欧式距离后，可以借助 KDTree（KNN算法用到）或者 BallTree（对高维向量友好）来降低复杂度。

欧氏距离和余弦相似度的区别是什么？另一个总结几种距离度量方法比较

线性回归

岭回归、Lasso回归和弹性网络回归

逻辑回归

回归划分

广义线性模型家族里，依据因变量不同，可以有如下划分：

如果是连续的，就是多重线性回归
如果是二项分布(0-1分布)，就是逻辑回归
如果是泊松(Poisson)分布，就是泊松回归
如果是负二项分布，就是负二项回归
逻辑回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最常用的就是二分类的逻辑回归。

逻辑回归适用性

用于概率预测。用于可能性预测时，得到的结果有可比性。比如根据模型进而预测在不同的自变量情况下，发生某病或某种情况的概率有多大。
用于分类。实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。进行分类时，仅需要设定一个阈值即可，可能性高于阈值是一类，低于阈值是另一类。
寻找危险因素。寻找某一疾病的危险因素等。
仅能用于线性问题。只有当目标和特征是线性关系时，才能用逻辑回归。在应用逻辑回归时注意两点：一是当知道模型是非线性时，不适用逻辑回归；二是当使用逻辑回归时，应注意选择和目标为线性关系的特征。
各特征之间不需要满足条件独立假设，但各个特征的贡献独立计算。

逻辑回归与朴素贝叶斯的区别

逻辑回归是判别模型，朴素贝叶斯是生成模型，所以生成和判别的所有区别它们都有。

判别模型：由数据直接学习决策函数 $f(X)$ 或者条件概率分布 $P(Y|X)$ 做为预测的模型，即判别模型。判别方法关系的是对给定的输入 $X$，应该预测什么样的输出 $Y$
生成模型：由数据学习联合概率分布 $P(X, Y)$，然后求出条件概率分布 $P(Y|X)$ 作为预测的模型，即生成模型：　$P(Y|X) = \frac{P(X, Y)}{P(X)}$

朴素贝叶斯属于贝叶斯，逻辑回归是极大似然，两种概率哲学间的区别。
朴素贝叶斯需要条件独立假设。
逻辑回归需要求特征参数间是线性的。

逻辑回归与线性回归的联系与区别

联系： 线性回归与逻辑回归都是广义的线性回归

区别	线性回归（liner regression）	LR（logistics regression）
构建方法	最小二乘法	极大似然函数
解决问题	主要用于预测，解决回归问题也可以用来分类，但是鲁棒性差	解决分类问题
输出	输出实数域上连续值	输出值被S型函数映射到[0,1] 通过设置阈值转换成分类类别
拟合函数	$h_{\theta}(x)=\theta ^{T}x=\theta _{1}x _{1}+\theta _{2}x _{2}+...+\theta _{n}x _{n}$	$h_{\theta}(x)=P(y=1\|x;\theta )=g(\theta ^{T}x)$，其中，$g(z)=\frac{1}{1+e^{-z}}$

线性回归的拟合函数，是对 $h_{\theta}(x)$ 的输出变量 $y$ 的拟合（通过房屋大小，预测房价）
逻辑回归的拟合函数，通过已确定的参数，计算出输入变量 $y = 1$ 的可能性，即是对为1类样本的概率的拟合（疾病预测）

逻辑回归与 SVM 的联系与区别 *

相同点：

都是分类算法
都是监督学习算法
都是判别模型
如果不考虑核函数，LR 与 SVM 都是线性分类算法，也就是说他们的分类决策面都是线性的

不同点：

LR 和 SVM 的本质区别来自于 loss function的不同
LR 使用的是交叉熵损失函数/对数损失函数 (cross entropy / log loss)

\[ J(\theta)=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right] \]

SVM 是 合页损失函数 (hinge loss)

\[ \mathcal{L}(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{n} \alpha_{i}\left(y_{i}\left(w^{T} x_{i}+b\right)-1\right) \]

LR 基于概率理论，假设样本为1的概率可以用sigmoid函数来表示，然后通过极大似然估计的方法估计出参数的值。SVM 基于几何间隔最大化原理，认为存在最大几何间隔的分类面为最优分类面。线性SVM依赖数据表达的距离测度，所以需要对数据先做normalization，LR不受其影响
LR 可以产生概率，SVM 不能产生概率
SVM 只考虑局部的边界线附近的点，而逻辑回归考虑全局（远离的点对边界线的确定也起作用）
SVM的损失函数自带正则（结构风险最小化），而LR需要额外在损失函数上添加正则项

逻辑回归与随机森林区别

随机森林等树算法都是非线性的，而LR是线性的。LR更侧重全局优化，而树模型主要是局部的优化。

SVM

支持向量机（Support Vector Machines, SVM）是一种二分类模型。思想：间隔最大化来得到最优的分离超平面。方法：是将这个问题形式化为一个凸二次规划问题，也等价于一个正则化的合页损失函数最小化问题。其基本模型是定义在特征空间上的间隔最大的线性分类器。还可以通过使用核技巧，使其成为实质上的非线性分类器。SVM 的最优化算法是求解凸二次规划的最优化算法。

什么是支持向量

训练数据集中与分离超平面距离最近的样本点的实例称为支持向量
更通俗的解释：
数据集中的某些点，位置比较特殊。比如 x+y-2=0 这条直线，假设出现在直线上方的样本记为 A 类，下方的记为 B 类。
在寻找找这条直线的时候，一般只需看两类数据，它们各自最靠近划分直线的那些点，而其他的点起不了决定作用。
这些点就是所谓的“支持点”，在数学中，这些点称为向量，所以更正式的名称为“支持向量”。

SVM中支持向量的通俗解释！！！要结合这个一起看

支持向量机的分类

线性可分支持向量机
当训练数据线性可分时，通过硬间隔最大化，学习一个线性分类器，即线性可分支持向量机，又称硬间隔支持向量机。
线性支持向量机
当训练数据接近线性可分时，通过软间隔最大化，学习一个线性分类器，即线性支持向量机，又称软间隔支持向量机。
非线性支持向量机
当训练数据线性不可分时，通过使用核技巧及软间隔最大化，学习非线性支持向量机。

最大间隔超平面背后的原理

机器学习技法 (1-5) - 林轩田

相当于在最小化权重时对训练误差进行了约束——对比 L2 范数正则化，则是在最小化训练误差时，对权重进行约束

与 L2 正则化的区别

相当于限制了模型复杂度——在一定程度上防止过拟合，具有更强的泛化能力

支持向量机推导

SVM 由简至繁包括：线性可分支持向量机、线性支持向量机以及非线性支持向量机

一、线性可分支持向量机推导

《统计学习方法》 & 支持向量机SVM推导及求解过程 - CSDN博客

当训练数据线性可分时，通过硬间隔最大化，学习一个线性分类器，即线性可分支持向量机，又称硬间隔支持向量机。
线性 SVM 的推导分为两部分

如何根据间隔最大化的目标导出 SVM 的标准问题；
拉格朗日乘子法对偶问题的求解过程.

符号定义

训练集 $T$

\[ T= \{(x_{1}, y_{1}),(x_{2}, y_{2}), \cdots,(x_{N}, y_{N})\} \]

分离超平面 $(w, b)$

\[ w^{*} \cdot x+b^{*}=0 \]

如果使用映射函数，那么分离超平面为
\[ w^{*} \cdot \Phi(x)+b^{*}=0 \]

映射函数 $Φ(x)$ 定义了从输入空间到特征空间的变换，特征空间通常是更高维的，甚至无穷维；方便起见，这里假设 $Φ(x)$ 做的是恒等变换。

分类决策函数 $f(x)$

\[ f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right) \]

SVM 标准问题的推导

从“函数间隔”到“几何间隔”

在分离超平面 $w \cdot x+b =0$ 确定的情况下，$|w \cdot x+b|$ 能够相对地表示点 $x$ 距离超平面的远近. 而 $w \cdot x+b$ 的符号与类别标记 $y$ 的符号一致时表示分类正确。所以可以用 $y(w^{*} \cdot x+b^{*})$ 来表示分类的正确性，这就是 函数间隔

给定训练集 $T$ 和超平面 $(w, b)$

定义超平面关于样本点 $(x_i, y_i)$ 的函数间隔 $\hat{\gamma}_i$

\[ \hat{\gamma}_{i}=y_{i}\left(w \cdot x_{i}+b\right) \]

定义超平面 $(w, b)$ 关于数据集 $T$ 的 $\mathbf{\color{red}{函数间隔 \ \hat{\gamma}}}$ 为，超平面 $(w, b)$ 关于 $T$ 中所有样本点 $(x_i, y_i)$ 的函数间隔之最小值，即

\[ \begin{aligned} \hat{\gamma} &=\min _{i=1, \cdots, N} y_{i}\left(w \cdot x_{i}+b\right) \\ &=\min _{i=1, \cdots, N} \hat{\gamma}_{i} \end{aligned} \]

函数间隔如果成比例的改变 $w$ 和 $b$ (比如都扩大2倍)，此时超平面没有改变，但是函数间隔却成了原来的 2 倍。为此，可以对超平面的法向量 $w$ 进行规范化， $||w|| = 1$，使得间隔是确定的，这时的函数间隔就转换成为 几何间隔。（几何间隔最大的分离超平面是唯一的）

对 $w$ 作规范化，使函数间隔成为$\mathbf{\color{red}{几何间隔} \ \gamma}$
\[ \begin{aligned} \gamma &=\min _{i=1, \cdots, N} y_{i}\left(\frac{w}{\color{red}{\|w\|}} x_{i}+\frac{b}{\color{red}{\|w\|}}\right) \\ &=\min _{i=1, \cdots, N} \frac{\gamma_{i}}{\color{red}{\|w\|}} \end{aligned} \]

超平面关于样本点$(x_i, y_i)$ 的几何间隔，是实例点到超平面的带符号的距离，分类正确时，就是距离。

函数间隔 $\hat{\gamma}$ 和几何间隔 $\gamma$ 的关系：
\[ \gamma=\frac{\hat{\gamma}}{\|w\|} \]

最大化几何间隔

要得到最大间隔的分离超平面，即几何间隔最大的分离超平面。即可将问题表示为下面的约束最优化问题：
\[ \begin{array} {ll} &{\color{Red}{\underset{w,b}{\max}}} \quad \gamma \\ & {\mathrm{s.t.} \quad\ y_i(\frac{w}{\color{Red} {\| w \|}}x_i+\frac{b}{\color{Red} {|| w ||}}) \geq \gamma,\quad i=1,2,\cdots,N} \end{array} \]
即我们希望最大化超平面 $(w, b)$ 关于训练数据集的几何间隔 $\gamma$ ，约束条件表示的是超平面 $(w, b)$ 关于每个训练样本的几何间隔至少是 $\gamma$

由函数间隔与几何间隔的关系，等价于
\[ \begin{array}{ll} {\color{Red}{\underset{w,b}{\max}}} & {\frac{\hat{\gamma}}{\color{Red}{\|w\|}}} \\ {\text { s.t. }} & {y_{i}\left(w \cdot x_{i}+b\right) \geqslant \hat{\gamma}, \quad i=1,2, \cdots, N}\end{array} \]
函数间隔 $\hat{\gamma}$ 的取值不会影响最终的超平面 $(w, b)$ ，比如将 $w$ 和 $b$ 按比例改变为 $\lambda w$ 和 $\lambda b$，此时函数间隔为 $\lambda \hat{\gamma}$，此时的不等式约束没有影响，对目标函数的优化也没有影响，所以可取 $\hat{\gamma} = 1$

又最大化 $\frac{1}{\|w\|}$ 等价于最小化 $\frac{1}{2}\|w\|^{2}$，于是得到 $\mathbf{\color{red}{线性可分支持向量机的最优化问题，即SVM的标准问题}}$：
\[ \begin{array}{ll} {\color{Red}{\underset{w,b}{\min}}} & {\frac{1}{2} {\color{red}{ \|w\|^{2}}}} \\ {\text { s.t. }} & {y_{i}\left(w x_{i}+b\right) {\color{red}{-1}} \geq 0, \quad i=1,2, \cdots, N}\end{array} \\ {\color{green} {主问题（primal \ problem）}} \]

为什么令 $\hat{\gamma} = 1$？——比例改变 $(ω,b)$，超平面不会改变，但函数间隔 $\hat{\gamma}$ 会成比例改变，因此可以通过等比例改变 $(ω,b)$ 使函数间隔 $\hat{\gamma} = 1$

这是一个凸二次优化问题，这种带约束的最优化问题，我们可以使用拉格朗日乘子法来求解。并且可以自然的引入核函数，进而推广到非线性的情况。

凸优化问题是指约束最优化问题：
\[ \begin{array}{ll}{\min _{w}} & {f(w)} \\ {\text { s.t. }} & {g_{i}(w) \leqslant 0, \quad i=1,2, \cdots, k} \\ & {h_{i}(w)=0, \quad i=1,2, \cdots, l}\end{array} \]
其中，目标函数 $f(w)$ 约束函数 $g_i(w)$ 都是 $\mathbf{R}^{n}$ 上的连续可微的凸函数，约束函数 $h_i(w)$ 是 $\mathbf{R}^{n}$ 上的仿射函数。

当目标函数 $f(w)$ 是二次函数，且约束函数 $g_i(w)$ 是仿射函数时，上述凸优化问题成为凸二次规划问题。

$f(x)$ 称为仿射函数，如果它满足 $f(x) = a \cdot x + b, \quad a \in \mathbf{R}^{n}, \quad b \in \mathbf{R}, \quad x \in \mathbf{R}^{n}$

SVM 对偶算法的推导

构建拉格朗日函数
\[ \begin{aligned} L(w,b,{\color{Red} \alpha})=&\frac{1}{2}w^Tw-\sum_{i=1}^N{\color{Red} {\alpha_i}}[y_i(w^Tx_i+b)-1]\\ &{\color{Red}{\alpha_i \geq 0}},\quad i=1,2,\cdots,N \end{aligned} \]
标准问题是求极小极大问题：

\[ \begin{aligned} {\color{Red}{\underset{w,b}{\min}}}\ {\color{Blue} {\underset{\alpha}{\max}}}\ L(w,b,\alpha) \end{aligned} \]
其对偶问题为：

\[ \begin{aligned} {\color{Blue} {\underset{\alpha}{\max}}}\ {\color{Red} {\underset{w,b}{\min}}}\ L(w,b,\alpha) \end{aligned} \]

求 $L$ 对 $(w,b)$ 的极小

\[ \begin{aligned} \mathrm{set}\quad \frac{\partial L}{\partial w}=0 \;\;&\Rightarrow\; w-\sum_{i=1}^N {\color{Red}{\alpha_i y_i x_i}}=0\\ &\Rightarrow\; w=\sum_{i=1}^N {\color{Red} {\alpha_i y_i x_i}} \end{aligned} \]

\[ \begin{aligned} \mathrm{set}\quad \frac{\partial L}{\partial b}=0 \;\;&\Rightarrow\; \sum_{i=1}^N {\color{Red} {\alpha_i y_i}}=0 \end{aligned} \]

结果代入 $L$，有：
\[ \begin{aligned} L(w,b,{\color{Red} \alpha}) &=\frac{1}{2}w^Tw-\sum_{i=1}^N{\color{Red} {\alpha_i}}[y_i(w^Tx_i +b)-1]\\ &=\frac{1}{2}w^Tw-w^T\sum_{i=1}^N \alpha_iy_ix_i-b\sum_{i=1}^N \alpha_iy_i +\sum_{i=1}^N \alpha_i\\ &=\frac{1}{2}w^Tw-w^Tw +\sum_{i=1}^N \alpha_i\\ &=-\frac{1}{2}w^Tw +\sum_{i=1}^N \alpha_i\\ &=-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_j\cdot y_iy_j\cdot {\color{Red} {x_i^Tx_j}} +\sum_{i=1}^N \alpha_i \end{aligned} \]
即

\[ \min _{w, b} \quad L(w, b, \alpha)=-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} \cdot y_{i} y_{j} \cdot {\color{Red}{x_{i}^{T} x_{j}}}+\sum_{i=1}^{N} \alpha_{i} \]

求 $L$ 对 $α$ 的极大，即
\[ \begin{aligned} &\underset{\alpha}{\max} \quad -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_j\cdot y_iy_j\cdot x_i^Tx_j+\sum_{i=1}^N \alpha_i\\ &\ \mathrm{s.t.}\quad\; \sum_{i=1}^N \alpha_i y_i=0,\\ & \quad\; \quad\; \ {\color{Red} {\alpha_i \geq 0}},\quad i=1,2,\cdots,N \end{aligned} \]
该问题的对偶问题为：
\[ \begin{aligned} &{\color{Red} {\underset{\alpha}{\min}}} \quad\ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_j\cdot y_iy_j\cdot x_i^Tx_j-\sum_{i=1}^N \alpha_i\\ &\ \mathrm{s.t.}\quad\; \sum_{i=1}^N \alpha_i y_i=0, \\ & \ \quad\; \quad\; \ {\color{Red} {\alpha_i \geq 0}}, \quad i=1,2,\cdots,N \end{aligned} \]
于是，标准问题最后等价于求解该对偶问题

继续求解该优化问题，有 SMO 方法

SMO思想：先固定 $a_i$ 之外的所有参数，然后求 $a_i$ 上的极值。由于存在约束 $\sum^m_{i=1} a_i y_i = 0$，若固定 $a_i$ 之外的其他变量，则 $a_i$ 可由其他变量导出。于是，SMO不断执行如下两个步骤直至收敛：

选取一对需要更新的变量 $a_i$ 和 $a_j$

固定 $a_i$ 和 $a_j$ 以外的参数，求解上述对偶问题，获得更新后的 $a_i$ 和 $a_j$

设 $α$ 的解为 $α^*$，则存在下标 $j$ 使 $α_j > 0$，可得标准问题的解为：
\[ \begin{aligned} w^{*} &=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} \\ b^{*} &={\color{Red}{y_{j}}}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x_{i}^{T} {\color{Red}{x_{j}}}\right) \end{aligned} \]
可得分离超平面及分类决策函数为：
\[ \begin{array}{c}{w^{*} \cdot x+b^{*}=0} \\ {f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right)} \end{array} \]

二、线性支持向量机

当训练数据接近线性可分时，训练数据中有一些异常点，将这些异常点去除后，剩下的大部分的样本点组成的集合是线性可分的。通过软间隔最大化，学习一个线性分类器，即线性支持向量机，又称软间隔支持向量机。

通过增加松弛因子 $\xi_{i} \geq 0$ 使函数间隔加上松弛变量大于等于1，则约束条件变成：
\[ y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i} \]
对每个松弛变量 $\xi_{i}$，添加一个代价，目标函数为：
\[ \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} \]
$C > 0$ 为惩罚参数，$C$ 值大时对误分类的惩罚增大，$C$ 值小时对误分类的惩罚减小。即最小化目标函数包含两层含义：使 $\frac{1}{2}||w||^2$ 尽量小即间隔尽量大，同事使误分类点的个数尽量小，$C$ 是调和二者的系数。

$\mathbf{\color{red}{线性支持向量机的最优化问题}}$

\[ \begin{array}{ll}{\color{red}{\underset{w, b, \xi}{\min}}} & {\frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i}} \\ {\text { s.t. }} & {y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N} \\ {} & {\xi_{i} \geqslant 0, \quad i=1,2, \cdots, N}\end{array} \]

构造拉格朗日函数

\[ L(w, b, \xi, \alpha, \mu) = \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i}-\sum_{i=1}^{N} \alpha_{i}\left(y_{i}\left(w \cdot x_{i}+b\right)-1+\xi_{i}\right)-\sum_{i=1}^{N} \mu_{i} \xi_{i} \\ 其中，\alpha_{i} \geqslant 0, \mu_{i} \geqslant 0 \]

对 $w, b, \xi$ 求偏导

\[ \begin{array}{l}{\frac{\partial L}{\partial w}=0 \Rightarrow w=\sum_{i=1}^{n} \alpha_{i} y_{i} x_{i}} \\ {\frac{\partial L}{\partial b}=0 \Rightarrow \sum_{i=1}^{n} \alpha_{i} y_{i}} = 0 \\ {\frac{\partial L}{\partial \xi}=0 \Rightarrow C-\alpha_{i}-u_{i}=0}\end{array} \]

将三式带入 $L$ 中，得

\[ {\color{red}{\min _{w, b, \xi}}} \ L(w, b, \xi, \alpha, \mu)=-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \]

再对 ${\color{red}{\underset{w, b, \xi}{\min}}} \ L(w, b, \xi, \alpha, \mu)$ 求 $a$ 的极大，即得对偶问题：

\[ \begin{aligned} & {\color{blue}{\max _{\alpha}}} \quad\ -\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \\ &\ \mathrm{s.t.}\quad\; \sum_{i=1}^N \alpha_i y_i=0, \end{aligned} \]

\[ \begin{array}{l}{C-\alpha_{i}-u_{i}=0} \\ {\alpha_{i} \geq 0} \\ {u_{i} \geq 0, i=1,2, \cdots, n}\end{array} \} \Rightarrow 0 \leq \alpha_{i} \leq C \]

整理得到对偶问题的最优化问题：

\[ \begin{aligned} &{\color{red}{\min _{\alpha}}} \quad\ \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} x_{j}\right)-\sum_{i=1}^{n} \alpha_{i} \\ & s.t. \quad\ \sum^n_{i = 1} a_i y_i \\ & \quad\ \quad\ \ 0 \leq \alpha_{i} \leq C, i=1,2, \cdots, N \end{aligned} \]

求得最优解 $a^*$，则存在下标 $j$ 使 $0 < α_j < C$，可得标准问题的解为：
\[ \begin{aligned} w^{*} &=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} \\ b^{*} &={\color{Red}{y_{j}}}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x_{i}^{T} {\color{Red}{x_{j}}}\right) \end{aligned} \]
可得分离超平面及分类决策函数为：
\[ \begin{array}{c}{w^{*} \cdot x+b^{*}=0} \\ {f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right)} \\ \end{array} \]

三、核函数

引入核函数目的：把原坐标系里线性不可分的数据用核函数Kernel投影到另一个空间，尽量使得数据在新的空间里线性可分。

核函数表示将输入从输入空间映射到特征空间后得到的特征向量之间的内积

核函数方法的广泛应用，与其特点是分不开的：

1）核函数的引入避免了“维数灾难”，大大减小了计算量。而输入空间的维数n对核函数矩阵无影响。因此，核函数方法可以有效处理高维输入。

2）无需知道非线性变换函数Φ的形式和参数。

3）核函数的形式和参数的变化会隐式地改变从输入空间到特征空间的映射，进而对特征空间的性质产生影响，最终改变各种核函数方法的性能。

4）核函数方法可以和不同的算法相结合，形成多种不同的基于核函数技术的方法，且这两部分的设计可以单独进行，并可以为不同的应用选择不同的核函数和算法。

常见的核函数

SVM为什么用对偶问题来求解

对偶问题将原始问题中的约束转为了对偶问题中的等式约束
方便核函数的引入
改变了问题的复杂度。由求特征向量 $w$ 转化为求比例系数 $a$，在原始问题下，求解的复杂度与样本的维度有关，即 $w$ 的维度。在对偶问题下，只与样本数量有关。
求解更高效，因为只用求解比例系数 $a$，而比例系数 $a$ 只有支持向量才为非0，其他全为0.

为何令间隔为1

什么是拉格朗日对偶

什么是KKT条件

http://whatbeg.com/2017/04/13/svmlearning.html

* 反向传播

KNN

给定一个训练数据集，对于新输入的实例，在训练数据集中找到与该实例最近的 $k$ 个实例，这 $k$ 个实例属于哪个类最多，就把该输入实例分为那个类。

决策树

决策树是一种基本的分类与回归方法。学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型。测试时，对新的数据集，利用决策树模型进行分类。
决策树是一种自上而下，对样本数据进行树形分类的过程，由结点和有向边组成。结点分为内部结点和叶结点，其中每个内部结点表示一个特征或属性，叶结点表示类别。从顶部根结点开始，所有样本聚在一起。经过根结点的划分，样本被分到不同的子结点中。再根据子结点的特征进一步划分，直至所有样本都被归到某一个类别（即叶结点）中。

决策树的三要素

决策树的训练通常由三部分组成：特征选择、树的生成、剪枝

特征选择：从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准，如何选择特征有着很多不同量化评估标准，从而衍生出不同的决策树算法。
树的生成：根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则决策树停止生长。
剪枝：决策树容易过拟合，一般来需要剪枝，缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。

剪枝处理的作用及策略

作用：缩小树的规模、缓解过拟合问题。

在决策树算法中，为了尽可能正确分类训练样本，节点划分过程不断重复，有时候会造成决策树分支过多，以至于将训练样本集自身特点当作泛化特点，而导致过拟合。因此可以采用剪枝处理来去掉一些分支来降低过拟合的风险。

剪枝的基本策略有预剪枝(pre-pruning) 和后剪枝(post-pruning)

预剪枝：在决策树生成过程中，在每个节点划分前先估计其划分后的泛化性能，如果不能提升，则停止划分，将当前节点标记为叶结点。
后剪枝：生成决策树以后，再自下而上对非叶结点进行考察，若将此节点标记为叶结点可以带来泛化性能提升，则修改之。

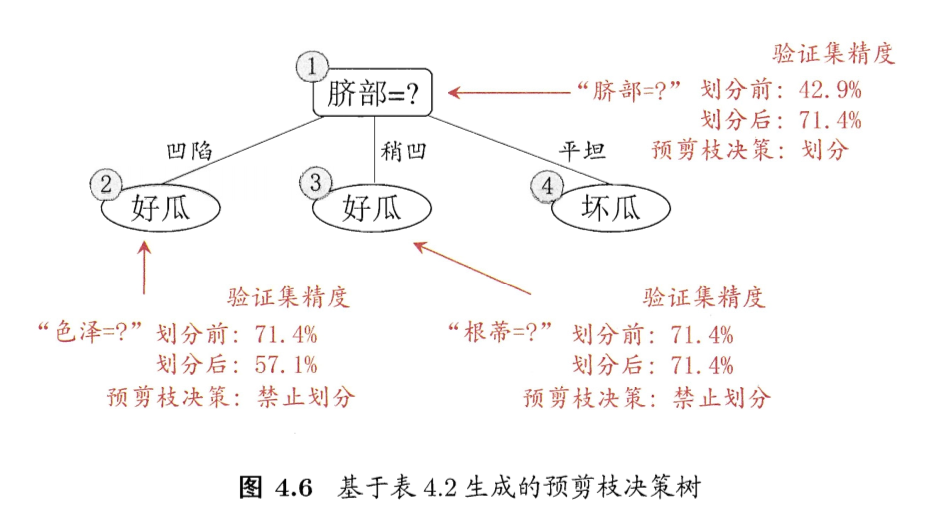
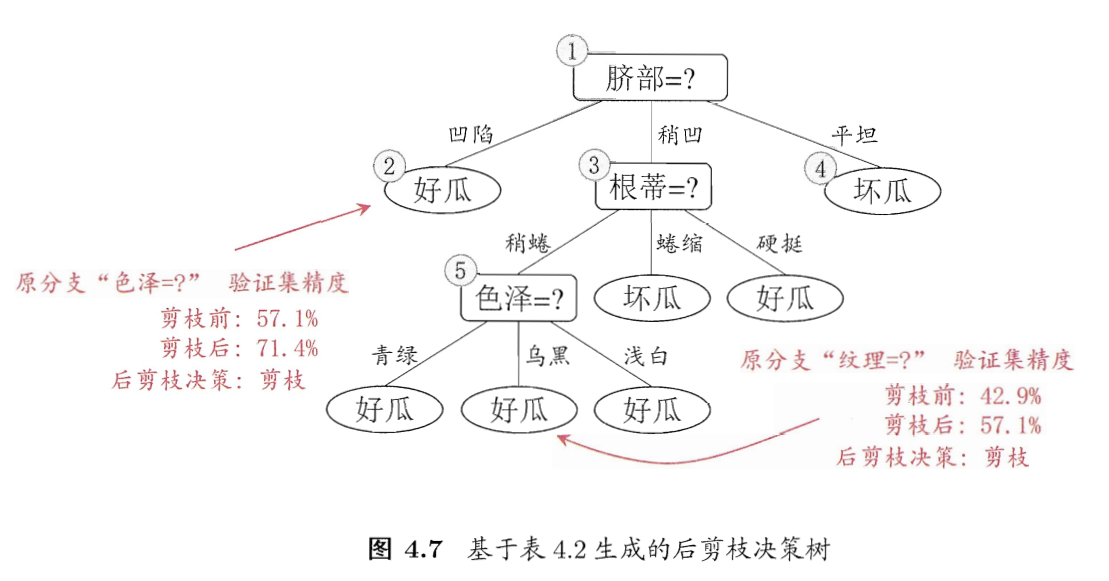
决策树学习基本算法

[分类树] ID3 决策树与 C4.5 决策树

ID3 决策树和 C4.5 决策树的区别在于：前者使用 信息增益 来进行特征选择，而后者使用 信息增益比。

[回归树] - CART 决策树

CART 使用 基尼指数 来选择属性划分

熵

熵：度量随机变量的不确定性。
定义：假设随机变量 $X$ 的可能取值有 $x_{1},x_{2},...,x_{n}$，对于每一个可能的取值 $x_{i}$，其概率为$P(X=x_{i})=p_{i}, \ \ i=1,2, ...n$。随机变量的熵为：
\[ H(X)=-\sum_{i=1}^{n}p_{i}log_{2}p_{i} \]
对于样本集合 $D$，类别数为 $K$，每个类别的概率为$\frac{|C_{k}|}{|D|}$，其中 ${|C_{k}|}$为类别为 $k$ 的样本个数，$|D|$为样本总数。样本集合 $D$ 的熵为：
\[ H(D)=-\sum_{k=1}^{K}\frac{|C_{k}|}{|D|}log_{2}\frac{|C_{k}|}{|D|} \]

条件熵

计算某个特征 $A$ 对于数据集 $D$ 的条件熵 $H(D|A)$ 为：
\[ H(D | A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D |}\left(-\sum_{k=1}^{K} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log _{2} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|}\right) \]
其中， $D_i$ 表示 $D$ 中特征 $A$ 取第 $i$ (年龄、长相、工资、写代码)个值的样本子集， $D_{ik}$ 表示 $D_i$ 中属于第 $k$ (见、不见)类的样本子集。

信息增益

定义：以某特征划分数据集前后的熵的差值。

以表示样本集合的不确定性，熵越大，样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合 $D$ 划分效果的好坏。

假设划分前样本集合 $D$ 的熵为 $H(D)$ 。使用某个特征 $A$ 划分数据集 $D$，计算划分后的数据子集的熵为 $H(D|A)$。
则信息增益为：
\[ g(D,A)=H(D)-H(D|A) \]

注：在决策树构建的过程中我们总是希望集合往最快到达纯度更高的子集合方向发展，因此我们总是选择使得信息增益最大的特征来划分当前数据集 $D$。

思想：计算所有特征划分数据集 $D$，得到多个特征划分数据集 $D$ 的信息增益，从这些信息增益中选择最大的，因而当前结点的划分特征便是使信息增益最大的划分所使用的特征。
缺点：信息增益对取值数目较多的属性有所偏好
举例说明

假设共有5个人追求场景中的女孩，年龄有两个属性（老，年轻），长相有三个属性（帅，一般，丑），工资有三个属性（高，中等，低），会写代码有两个属性（会，不会），最终分类结果有两类（见，不见）。我们根据女孩有监督的主观意愿可以得到下表：

	年龄	长相	工资	写代码	类别
小A	老	帅	高	不会	不见
小B	年轻	一般	中等	会	见
小C	年轻	丑	高	不会	不见
小D	年轻	一般	高	会	见
小L	年轻	一般	低	不会	不见

（1）首先计算数据集 $D$ 的信息熵
\[ H(D)=-\sum_{k=1}^{K}\frac{|C_{k}|}{|D|}log_{2}\frac{|C_{k}|}{|D|} \ \ \ \ \ ，(k：见/不见) \]

\[ H(D)=-\frac{3}{5} \log _{2} \frac{3}{5}-\frac{2}{5} \log _{2} \frac{2}{5}=0.971 \]

（2）然后计算每个特征对数据集的条件熵：
\[ H(D | A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D |}\left(-\sum_{k=1}^{K} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log _{2} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|}\right) \]

\[ \begin{align*} H(D|年龄) & = \frac{1}{5}H(老) + \frac{4}{5}H(年轻) \\ & =\frac{1}{5}(-0)+\frac{4}{5}\left(-\frac{2}{4} \log _{2} \frac{2}{4}-\frac{2}{4} \log _{2} \frac{2}{4}\right)=0.8 \\ H(D|长相) & = \frac{1}{5}H(帅) + \frac{3}{5}H(一般) + \frac{1}{5}H(丑) \\ & =0+\frac{3}{5}\left(-\frac{2}{3} \log _{2} \frac{2}{3}-\frac{1}{3} \log _{2} \frac{1}{3}\right)+0=0.551 \\ H(D|工资) & = \frac{1}{5}H(高) + \frac{3}{5}H(中等) + \frac{1}{5}H(低) \\ & =\frac{3}{5}\left(-\frac{2}{3} \log _{2} \frac{2}{3}-\frac{1}{3} \log _{2} \frac{1}{3}\right)+0+0=0.551 \\ H(D|写代码) & = \frac{3}{5}H(不会) + \frac{2}{5}H(会) \\ & =\frac{3}{5}(0)+\frac{2}{5}(0)=0 \end{align*} \]

（3）然后计算每个特征的信息增益：
\[ g(D,A)=H(D)-H(D|A) \]

\[ g(D, 年龄) = H(D) - H(D|年龄) = 0.971 - 0.8 = 0.171 \\ g(D|长相) = 0.42 \\ g(D|工资) = 0.42 \\ g(D|写代码) = 0.971 \]

信息增益率

（2）信息增益率

信息增益率本质：在信息增益的基础之上乘上一个惩罚参数。特征个数较多时，惩罚参数较小；特征个数较少时，惩罚参数较大。
惩罚参数：数据集 $D$ 以特征 $A$ 作为随机变量的熵的倒数。
\[ {\color{red}{信息增益率}} = {\color{red}{惩罚参数}} \times {\color{red}{信息增益}} \\ \begin{align*} 信息增益率：& g_{R}(D, A)=\frac{g(D, A)}{H_{A}(D)} \\ 数据集D以A作为随机变量的熵(取值熵)：&H_{A}(D)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D |} \log _{2} \frac{\left|D_{i}\right|}{|D|}\\ (惩罚参数的倒数) \end{align*} \]

缺点：信息增益率对取值数目较少的属性有所偏好
所以 C4.5 算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

计算数据集 $D$ 关于每个特征的取值熵：
\[ H_{年龄}(D) = -\frac{1}{5}log_2\frac{1}{5} - \frac{4}{5}log_2\frac{4}{5} = 0.722 \\ H_{长相}(D) = -\frac{1}{5}log_2\frac{1}{5} - \frac{3}{5}log_2\frac{3}{5} - \frac{1}{5}log_2\frac{1}{5}= 1.371 \\ H_{工资}(D) = -\frac{3}{5}log_2\frac{3}{5} - \frac{1}{5}log_2\frac{1}{5} - \frac{1}{5}log_2\frac{1}{5}= 1.371 \\ H_{年龄}(D) = -\frac{3}{5}log_2\frac{3}{5} - \frac{2}{5}log_2\frac{2}{5} = 0.971 \]
然后计算各个特征的信息增益率：
\[ g_R(D, 年龄) = 0.236， g_R(D, 长相) = 0.402 \\ g_R(D, 工资) =0.402， g_R(D, 写代码) = 1 \]
信息增益比最大的仍是特征“写代码”，但通过信息增益比，特征“年龄”对应的指标上升了，而特征“长相”和特征“工资”却有所下降。

最大基尼指数（Gini）

Gini 描述的是数据的纯度，与信息熵含义类似。
\[ \operatorname{Gini}(D)=1-\sum_{k=1}^{K}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2} \]
CART 在每一次迭代中选择基尼指数最小的特征及其对应的切分点进行分类。但与ID3、 C4.5不同的是， CART是一颗二叉树，采用二元切割法，每一步将数据按特征A的取值切成两份，分别进入左右子树。 特征 $A$ 的Gini指数 定义为：
\[ \operatorname{Gini}(D | A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \operatorname{Gini}\left(D_{i}\right) \]
计算各个特征的 Gini 指数：
\[ Gini(D|年龄=老) = 0.4，Gini(D|年龄=年轻) = 0.4 \\ Gini(D|长相=帅) = 0.4，Gini(D|长相=丑) = 0.4 \\ Gini(D|写代码=会) = 0，Gini(D|写代码=不会) = 0 \\ Gini(D|工资=高) = 0.47，Gini(D|工资=中等) = 0.3，Gini(D|工资=低) = 0.4 \]
在“年龄”“长相”“工资”“写代码”四个特征中，我们可以很快地发现特征“写代码”的Gini指数最小为0，因此选择特征“写代码”作为最优特征， “写代码=会”为最优切分点。按照这种切分，从根结点会直接产生两个叶结点，基尼指数降为0，完成决策树生长。

ID3、C4.5、CART决策树区别与联系

决策树算法优缺点

优点：

易理解，解释起来简单
可以用于小数据集
复杂度较小，为用于训练决策树的数据点的对数
能够处理多输出的问题
对缺失值不敏感
可以处理不相关特征数据
效率高，决策树只需要一次构建，反复使用，每一次预测的最大计算次数不超过决策树的深度
相比于其他算法智能分析一种类型变量，决策树算法可处理数字和数据的类别

缺点：

对连续性的字段比较难预测
容易出现过拟合
当类别太多时，错误可能就会增加的比较快
在处理特征关联性比较强的数据时表现得不是太好
对于各类别样本数量不一致的数据，在决策树当中，信息增益的结果偏向于那些具有更多数值的特征

朴素贝叶斯

概率知识

条件概率

设 $P(A) > 0$ ，条件概率为：$P(B|A) = \frac{P(AB)}{P(A)}$，称为在 $A$ 发生条件下，$B$ 发生的概率

乘法公式

① $P(AB) = P(A) \cdot P(B|A)$

② $P(ABC) = P(A) \cdot P(B|A) \cdot P(C|AB)$

独立性

全概率公式

贝叶斯公式

图解极大似然估计

极大似然估计的原理，用一张图片来说明，如下图所示：

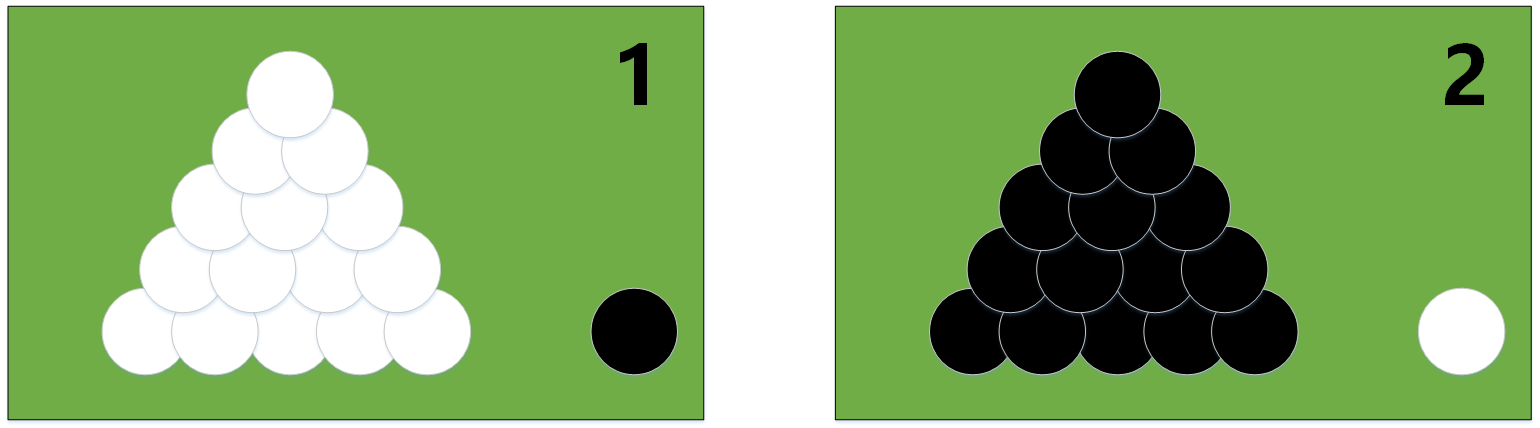
例：有两个外形完全相同的箱子，1号箱有99只白球，1只黑球；2号箱有1只白球，99只黑球。在一次实验中，取出的是黑球，请问是从哪个箱子中取出的？

一般的根据经验想法，会猜测这只黑球最像是从2号箱取出，此时描述的“最像”就有“最大似然”的意思，这种想法常称为“最大似然原理”。

极大似然估计原理

总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

极大似然估计是建立在极大似然原理的基础上的一个统计方法。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

由于样本集中的样本都是独立同分布，可以只考虑一类样本集$D$，来估计参数向量 $\vec\theta$。记已知的样本集为：
\[ D=\vec x_{1},\vec x_{2},...,\vec x_{n} \]
似然函数（likelihood function）：联合概率密度函数 $p(D|\vec\theta )$ 称为相对于 $\vec x_{1},\vec x_{2},...,\vec x_{n}$ 的 $\vec\theta$ 的似然函数。
\[ l(\vec\theta )=p(D|\vec\theta ) =p(\vec x_{1},\vec x_{2},...,\vec x_{n}|\vec\theta )=\prod_{i=1}^{n}p(\vec x_{i}|\vec \theta ) \]
如果 $\hat{\vec\theta}$ 是参数空间中能使似然函数 $l(\vec\theta)$ 最大的 $\vec\theta$ 值，则 $\hat{\vec\theta}$ 应该是“最可能”的参数值，那么 $\hat{\vec\theta}$ 就是$\theta$的极大似然估计量。它是样本集的函数，记作：
\[ \hat{\vec\theta}=d(D)= \mathop {\arg \max}_{\vec\theta} l(\vec\theta ) \]
$\hat{\vec\theta}(\vec x_{1},\vec x_{2},...,\vec x_{n})$ 称为极大似然函数估计值。

朴素贝叶斯

朴素贝叶斯法是基于 贝叶斯定理 和 特征条件独立假设 的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对给定的输入 $x$，利用贝叶斯定理求出后验概率最大的输出 $y$ .

输入空间 $\mathcal{X} \subseteq \mathbf{R}^{n}$ 为 $n$ 维向量的集合，输出空间为类别标记集合 $\mathcal{Y}=\left\{c_{1}\right. c_2, ..., c_k \}$. 输入特征向量$x \in \mathcal{X}$ ，输入为类别标记 $y \in \mathcal{Y}$. $X$ 是定义在输入空间上的随机向量， $Y$ 是定义在输出空间 $\mathcal{Y}$ 上的随机变量. $P(X, Y)$ 是 $X$ 和 $Y$ 的联合概率分布.

训练数据集： $T = \{(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\}$ ，由 $P(X, Y)独立同分布产生$.

朴素贝叶斯算法流程：

计算 先验概率

\[ P\left(Y=c_{k}\right), \quad k=1,2, \cdots, K \]

计算 条件概率

\[ \begin{aligned} P\left(X=x | Y=c_{k}\right) &=P\left(X^{(1)}=x^{(1)}, \cdots, X^{(n)}=x^{(n)} | Y=c_{k}\right) \\ &=\prod_{j=1}^{n} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right) \end{aligned} \\ \color{red}{(朴素贝叶斯对条件概率分布作了条件独立性假设)} \]

从而学习到联合概率分布 $P(X, Y)$。朴素贝叶斯法实际上学习到生成数据的机制，所以属于生成模型。条件独立假设等于说用于分类的特征在类确定的条件下都是条件独立的。

根据贝叶斯定理，将后验概率最大的类作为 $x$ 的类输出

\[ 贝叶斯定理： P(Y = c_k | X = x) = \frac{P(X = x|Y = c_k) P(Y = c_k)}{\sum_{k}P(X = x|Y = c_k)P(Y = c_k)} \]

\[ P\left(Y=c_{k} | X=x\right)=\frac{P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right)}{\sum_{k} P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right)}, \quad k=1,2, \cdots, K \]

以上是朴素贝叶斯法分类的基本公式。于是，朴素贝叶斯分类器可以表示为：
\[ y=f(x)=\arg \max _{c_{k}} \frac{P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right)}{\sum_{k} P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right)} \]
注意到，公式中分母对所有的 $c_k$ 都是相同的，所以：
\[ y=\arg \max _{a} P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} | Y=c_{k}\right) \]

举例说明

试由下表的训练数据学习一个朴素贝叶斯分类器，并确定 $x = (2, S)^T$ 的类的标记 $y$. 表中 $X^{1}, X{2}$ 为特征，取值的集合分别为 $A_1 = \{1, 2, 3\}, A_2 = \{S, M, L\}, Y$ 为类标记，$Y \in C=\{1,-1\}$

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
$X^{(1)}$	1	1	1	1	1	2	2	2	2	2	3	3	3	3	3
$X^{(2)}$	$S$	$M$	$M$	$S$	$S$	$S$	$M$	$M$	$L$	$L$	$L$	$M$	$M$	$L$	$L$
$Y$	-1	-1	1	1	-1	-1	-1	1	1	1	1	1	1	1	-1

计算先验概率

$P(Y=1)=\frac{9}{15}, \quad P(Y=-1)=\frac{6}{15}$

计算条件概率

$P\left(X^{(1)}=1 | Y=1\right)=\frac{2}{9}, \quad \quad P\left(X^{(1)}=2 | Y=1\right)=\frac{3}{9}, \quad \quad P\left(X^{(1)}=3 | Y=1\right)=\frac{4}{9}$
$P\left(X^{(2)}=S | Y=1\right)=\frac{1}{9}, \quad \quad P\left(X^{(2)}=M | Y=1\right)=\frac{4}{9}, \ \quad P\left(X^{(2)}=L | Y=1\right)=\frac{4}{9}$
$P\left(X^{(1)}=1 | Y=-1\right)=\frac{3}{6}, \ \quad P\left(X^{(1)}=2 | Y=-1\right)=\frac{2}{6}, \ \quad P\left(X^{(1)}=3 | Y=-1\right)=\frac{1}{6}$
$P\left(X^{(2)}=S | Y=-1\right)=\frac{3}{6}, \ \quad P\left(X^{(2)}=M | Y=-1\right)=\frac{2}{6}, \quad P\left(X^{(2)}=L | Y=-1\right)=\frac{1}{6}$

对于给定的 $x = (2, S)^T$，计算：
\[ \begin{array}{l}{P(Y=1) P\left(X^{(i)}=2 | Y=1\right) P\left(X^{(2)}=S | Y=1\right)=\frac{9}{15} \cdot \frac{3}{9} \cdot \frac{1}{9}=\frac{1}{45}} \\ {P(Y=-1) P\left(X^{(1)}=2 | Y=-1\right) P\left(X^{(2)}=S | Y=-1\right)=\frac{6}{15} \cdot \frac{2}{6} \cdot \frac{3}{6}=\frac{1}{15}}\end{array} \]
因为 $P(Y=-1) P\left(X^{(1)}=2 | Y=-1\right) P\left(X^{(2)}=S | Y=-1\right)$ 最大，所以 $y = -1$ .

K-means

算法流程

K-means 是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。
K-means 是一个迭代算法，假设我们想要将数据聚类成 $n$ 个组，其方法为:
（1）首先选择 $K$ 个随机的点，称为聚类中心（ cluster centroids）
（2）对于数据集中的每一个数据，按照距离 $K$ 个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类。
（3）计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置。
（4）重复步骤 2-4 直至中心点不再变化。

伪代码实现

import numpy as np
# 迭代方式计算样本点所属聚类中心索引
def findClosestCentroids(x, cent):
    k = np.size(cent, 0)
    idx = np.zeros((np.size(x, 0),), dtype=int)
    dist = np.zeros((k, 1))
    m = np.size(x, 0)
    for i in range(m):
        for j in range(k):
            dist[j] = np.sum((x[i, :] - cent[j, :])**2)
        idx[i] = np.argmin(dist)
    return idx

# 更新每组聚类中心
def computeCentroids(x, idx, k):
    m, n = np.shape(x)
    cent = np.zeros((k, n))
    for i in range(k):
        x_idx = np.where(idx == i)
        cent[i, :] = np.sum(x[x_idx], 0) / np.size(x[x_idx], 0)
    return cent

K值的选择手肘法

手肘法的核心指标是SSE(sum of the squared errors，误差平方和)
\[ S S E=\sum_{i=1}^{k} \sum_{p \in C_{i}}\left|p-m_{i}\right|^{2} \]
其中，$C_i$ 是第 $i$ 个簇，$p$ 是 $C_i$ 中的样本点，$m_i$ 是 $C_i$ 的质心（Ci中所有样本的均值），SSE是所有样本的聚类误差，代表了聚类效果的好坏。

手肘法的核心思想是：随着聚类数 $k$ 的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当 $k$ 小于真实聚类数时，由于 $k$ 的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当 $k$ 到达真实聚类数时，再增加 $k$ 所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着 $k$ 值的继续增大而趋于平缓，也就是说SSE和 $k$ 的关系图是一个手肘的形状，而这个肘部对应的 $k$ 值就是数据的真实聚类数。当然，这也是该方法被称为手肘法的原因。

PCA

思想总结

PCA就是将高维的数据通过线性变换投影到低维空间上去。
投影思想：找出最能够代表原始数据的投影方法，最大化样本的投影方差。被 PCA 降掉的那些维度只能是那些噪声或是冗余的数据。

算法总结

输入：$n$ 维样本集 $D = \left( x^{(1)},x^{(2)},...,x^{(m)} \right)$ ，目标降低到 $k$ 维

输出：降维后的新样本集 $D' = \left( z^{(1)},z^{(2)},...,z^{(m)} \right)$ 。

主要步骤如下：

对所有的样本进行归一化，$x^{(i)} = x^{(i)} - \frac{1}{m} \sum^m_{j=1} x^{(j)}$ ，如果特征是不同的数量级上，我们还要将其除以标准差
计算样本的协方差矩阵 $XX^T$
对协方差矩阵 $XX^T$ 进行特征值分解（或奇异值分解）
取出最大的 $k$ 个特征值对应的特征向量 $\{ w_1,w_2,...,w_{n'} \}$
标准化特征向量，得到特征向量矩阵 $W$
转化样本集中的每个样本 $z^{(i)} = W^T x^{(i)}$
得到输出矩阵 $D' = \left( z^{(1)},z^{(2)},...,z^{(n)} \right)$ 。

注：在降维时，有时不明确目标维数，而是指定降维到的主成分比重阈值 $k(k \epsilon(0,1])$ 。假设 $n$ 个特征值为 $\lambda_1 \geqslant \lambda_2 \geqslant ... \geqslant \lambda_n$ ，则 $n'$ 可从 $^{n’}_{i=1} i k ^n{i=1} _i $ 得到。

层次聚类

1 .算法

假设有 n 个待聚类的样本，对于层次聚类算法，它的步骤是：

步骤一：（初始化）将每个样本都视为一个聚类；
步骤二：计算各个聚类之间的相似度；
步骤三：寻找最近的两个聚类，将他们归为一类；
步骤四：重复步骤二，步骤三；直到所有样本归为一类。

整个过程就是建立一棵树，在建立的过程中，可以在步骤四设置所需分类的类别个数，作为迭代的终止条件，毕竟都归为一类并不实际。

2 . 聚类之间的相似度

聚类和聚类之间的相似度有什么来衡量呢？既然是空间中的点，可以采用距离的方式来衡量，一般有下面三种：

Single Linkage

又叫做 nearest-neighbor ，就是取两个类中距离最近的两个样本的距离作为这两个集合的距离。这种计算方式容易造成一种叫做 Chaining 的效果，两个 cluster 明明从“大局”上离得比较远，但是由于其中个别的点距离比较近就被合并了，并且这样合并之后 Chaining 效应会进一步扩大，最后会得到比较松散的 cluster 。

Complete Linkage

这个则完全是 Single Linkage 的反面极端，取两个集合中距离最远的两个点的距离作为两个集合的距离。其效果也是刚好相反的，限制非常大。这两种相似度的定义方法的共同问题就是指考虑了某个有特点的数据，而没有考虑类内数据的整体特点。

Average Linkage 这种方法就是把两个集合中的点两两的距离全部放在一起求均值，相对也能得到合适一点的结果。有时异常点的存在会影响均值，平常人和富豪平均一下收入会被拉高是吧，因此这种计算方法的一个变种就是取两两距离的中位数。

3 . 层次聚类的优缺点

优点：

一次性得到聚类树，后期再分类无需重新计算；
相似度规则容易定义；
可以发现类别的层次关系。

缺点：

计算复杂度高，不适合数据量大的；
算法很可能形成链状。

Reference: 1 2

LDA

线性判别分析（Linear Discriminant Analysis，LDA）是一种经典的降维方法。和主成分分析 PCA 不考虑样本类别输出的无监督降维技术不同，LDA 是一种监督学习的降维技术，数据集的每个样本有类别输出。

LDA 分类思想

多维空间中，数据处理分类问题较为复杂，LDA 算法将多维空间中的数据投影到一条直线上，将 $d$ 维数据转化成 $1$ 维数据进行处理。
对于训练数据，设法将多维数据投影到一条直线上，同类数据的投影点尽可能接近，异类数据点尽可能远离。
对新数据进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定样本的类别。

如果用一句话概括LDA思想，即 “投影后类内方差最小，类间方差最大”

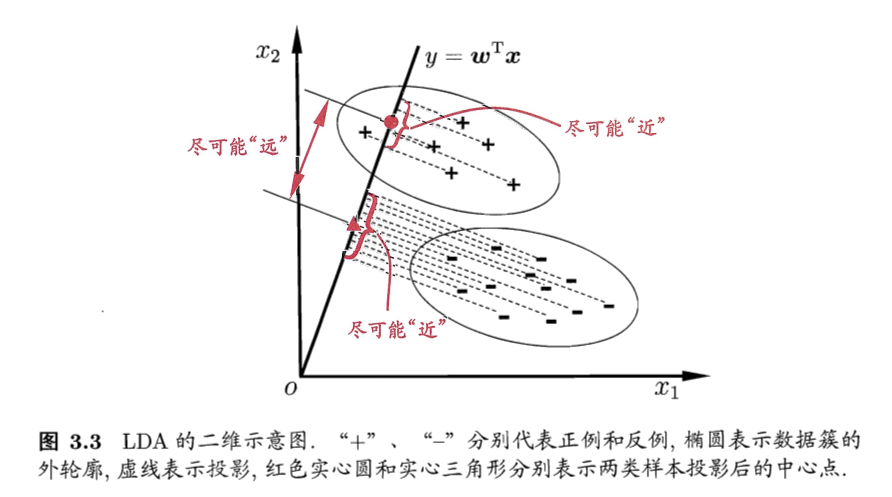
LDA 降维算法流程

输入：数据集 $D=\{(\boldsymbol x_1,\boldsymbol y_1),(\boldsymbol x_2,\boldsymbol y_2),...,(\boldsymbol x_m,\boldsymbol y_m)\}$，其中样本 $x_i $ 是 $n$ 维向量，$\boldsymbol y_i \epsilon \{0, 1\}$，降维后的目标维度 $d$ ，定义

$N_j(j=0,1)$ 为第 $j$ 类样本个数
$X_j(j=0,1)$ 为第 $j$ 类样本的集合
$u_j(j=0,1)$ 为第 $j$ 类样本的均值向量
$\sum_j(j=0,1)$ 为第 $j$ 类样本的协方差矩阵

其中
\[ u_j = \frac{1}{N_j} \sum_{\boldsymbol x\epsilon X_j}\boldsymbol x \ \ \ \ \ \ \ \ (j=0,1)， \\ \sum_j = \sum_{\boldsymbol x\epsilon X_j}(\boldsymbol x-u_j)(\boldsymbol x-u_j)^T \ \ \ \ \ (j=0,1) \]
假设投影直线是向量 $\boldsymbol w$，对任意样本 $\boldsymbol x_i$，它在直线 $\boldsymbol w$上的投影为 $\boldsymbol {w^Tx_i}$，两个类别的中心点 $u_0$, $u_1$在直线 $\boldsymbol w$ 的投影分别为 $\boldsymbol w^Tu_0$ 、$\boldsymbol w^Tu_1$。

LDA 的目标是让同类样例投影点尽可能近，既让同类样例投影点的协方差$\boldsymbol w^T \sum_0 \boldsymbol w$、$\boldsymbol w^T \sum_1 \boldsymbol w$ 尽量小，即最小化 $\boldsymbol w^T \sum_0 \boldsymbol w +\boldsymbol w^T \sum_1 \boldsymbol w$ 。而使异类样例的投影点尽可能远，即可让两类别的数据中心间的距离 $\| \boldsymbol w^Tu_0 - \boldsymbol w^Tu_1 \|^2_2$ 尽量大。

类内散度矩阵 $S_w$

\[ S_w = \sum_0 + \sum_1 = \sum_{\boldsymbol x\epsilon X_0}(\boldsymbol x-u_0)(\boldsymbol x-u_0)^T + \sum_{\boldsymbol x\epsilon X_1}(\boldsymbol x-u_1)(\boldsymbol x-u_1)^T \]
- 类间散度矩阵 $S_b$

\[ S_b = (u_0 - u_1)(u_0 - u_1)^T \]

据上分析，优化目标为
\[ \mathop{\arg\max}_\boldsymbol w J(\boldsymbol w) = \frac{\| \boldsymbol w^Tu_0 - \boldsymbol w^Tu_1 \|^2_2}{\boldsymbol w^T \sum_0\boldsymbol w + \boldsymbol w^T \sum_1\boldsymbol w} = \frac{\boldsymbol w^T(u_0-u_1)(u_0-u_1)^T\boldsymbol w}{\boldsymbol w^T(\sum_0 + \sum_1)\boldsymbol w} = \frac{\boldsymbol w^TS_b\boldsymbol w}{\boldsymbol w^TS_w\boldsymbol w} \]
根据广义瑞利商的性质，矩阵 $\frac{S_b}{S_w}$ 的最大特征值为 $J(\boldsymbol w)$ 的最大值，矩阵 $\frac{S_b}{S_w}$ 的最大特征值对应的特征向量即为 $\boldsymbol w$

LDA 降维算法流程总结

输入：数据集 $D = \{ (x_1,y_1),(x_2,y_2), ... ,(x_m,y_m) \}$，其中样本 $x_i $ 是 $n$ 维向量，$y_i \epsilon \{C_1, C_2, ..., C_k\}$，降维后的目标维度 $d$

输出：降维后的数据集 $ $

步骤：

计算类内散度矩阵 $S_w$
计算类间散度矩阵 $S_b$
计算矩阵 $\frac{S_b}{S_w}$
计算矩阵 $\frac{S_b}{S_w}$ 的最大的 $d$ 个特征值
计算 $d$ 个特征值对应的 $d$ 个特征向量，记投影矩阵为 $W$
转化样本集的每个样本，得到新样本 $P_i = W^Tx_i$
输出新样本集 $\overline{D} = \{ (p_1,y_1),(p_2,y_2),...,(p_m,y_m) \}$

LDA 和 PCA区别

异同点	LDA	PCA
相同点	1. 两者均可以对数据进行降维 2. 两者在降维时均使用了矩阵特征分解的思想； 3. 两者都假设数据符合高斯分布
不同点	有监督的降维方法	无监督的降维方法
	降维最多降到k-1维	降维多少没有限制
	可以用于降维，还可以用于分类	只用于降维
	选择分类性能最好的投影方向	选择样本点投影具有最大方差的方向
	更明确，更能反映样本间差异	目的较为模糊

EM

EM算法基本思想

最大期望算法（Expectation-Maximization algorithm, EM），是一类通过迭代进行极大似然估计的优化算法，通常作为牛顿迭代法的替代，用于对包含隐变量或缺失数据的概率模型进行参数估计。

最大期望算法基本思想是经过两个步骤交替进行计算：

第一步是计算期望（E），利用对隐藏变量的现有估计值，计算其最大似然估计值；
第二步是最大化（M），最大化在E步上求得的最大似然值来计算参数的值。
M步上找到的参数估计值被用于下一个E步计算中，这个过程不断交替进行。

EM算法推导

对于$m$个样本观察数据$x=(x^{1},x^{2},...,x^{m})$，现在想找出样本的模型参数$\theta$，其极大化模型分布的对数似然函数为：
\[ \theta = \mathop{\arg\max}_\theta\sum\limits_{i=1}^m logP(x^{(i)};\theta) \]
如果得到的观察数据有未观察到的隐含数据$z=(z^{(1)},z^{(2)},...z^{(m)})$，极大化模型分布的对数似然函数则为：
\[ \theta =\mathop{\arg\max}_\theta\sum\limits_{i=1}^m logP(x^{(i)};\theta) = \mathop{\arg\max}_\theta\sum\limits_{i=1}^m log\sum\limits_{z^{(i)}}P(x^{(i)}, z^{(i)};\theta) \tag{a} \]
由于上式不能直接求出 $\theta$，采用缩放技巧：
\[ \begin{align} \sum\limits_{i=1}^m log\sum\limits_{z^{(i)}}P(x^{(i)}, z^{(i)};\theta) & = \sum\limits_{i=1}^m log\sum\limits_{z^{(i)}}Q_i(z^{(i)})\frac{P(x^{(i)}, z^{(i)};\theta)}{Q_i(z^{(i)})} \\ & \geqslant \sum\limits_{i=1}^m \sum\limits_{z^{(i)}}Q_i(z^{(i)})log\frac{P(x^{(i)}, z^{(i)};\theta)}{Q_i(z^{(i)})} \end{align} \tag{1} \]
上式用到了 Jensen 不等式：
\[ log\sum\limits_j\lambda_jy_j \geqslant \sum\limits_j\lambda_jlogy_j\;\;, \lambda_j \geqslant 0, \sum\limits_j\lambda_j =1 \]
并且引入了一个未知的新分布$Q_i(z^{(i)})$。

此时，如果需要满足 Jensen 不等式中的等号，所以有：
\[ \frac{P(x^{(i)}, z^{(i)};\theta)}{Q_i(z^{(i)})} =c \ \ \ \ \ \ \ (c为常数) \]
由于$Q_i(z^{(i)})$是一个分布，所以满足
\[ \sum\limits_{z}Q_i(z^{(i)}) =1 \]
综上，可得：
\[ Q_i(z^{(i)}) = \frac{P(x^{(i)}， z^{(i)};\theta)}{\sum\limits_{z}P(x^{(i)}, z^{(i)};\theta)} = \frac{P(x^{(i)}, z^{(i)};\theta)}{P(x^{(i)};\theta)} = P( z^{(i)}|x^{(i)};\theta) \]
如果$Q_i(z^{(i)}) = P( z^{(i)}|x^{(i)};\theta)$ ，则第(1)式是我们的包含隐藏数据的对数似然的一个下界。如果我们能极大化这个下界，则也在尝试极大化我们的对数似然。即我们需要最大化下式：
\[ \mathop{\arg\max}_\theta \sum\limits_{i=1}^m \sum\limits_{z^{(i)}}Q_i(z^{(i)})log\frac{P(x^{(i)}， z^{(i)};\theta)}{Q_i(z^{(i)})} \]
简化得：
\[ \mathop{\arg\max}_\theta \sum\limits_{i=1}^m \sum\limits_{z^{(i)}}Q_i(z^{(i)})log{P(x^{(i)}, z^{(i)};\theta)} \]
以上即为EM算法的M步，$\sum\limits_{z^{(i)}}Q_i(z^{(i)})log{P(x^{(i)}, z^{(i)};\theta)}$可理解为$logP(x^{(i)}, z^{(i)};) $基于条件概率分布$Q_i(z^{(i)}) $的期望。以上即为EM算法中E步和M步的具体数学含义。

图解EM算法

考虑上一节中的（a）式，表达式中存在隐变量，直接找到参数估计比较困难，通过EM算法迭代求解下界的最大值到收敛为止。

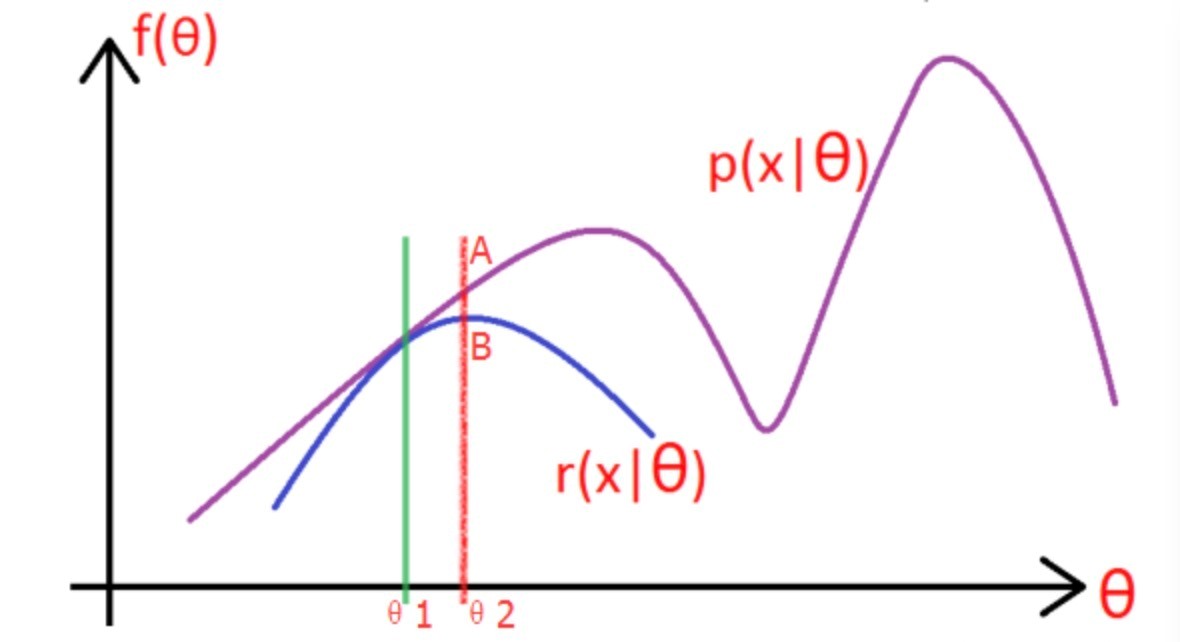
图片中的紫色部分是我们的目标模型 $p(x|\theta)$，该模型复杂，难以求解析解，为了消除隐变量 $z^{(i)}$ 的影响，我们可以选择一个不包含 $z^{(i)}$ 的模型 $r(x|\theta)$，使其满足条件 $r(x|\theta) \leqslant p(x|\theta) $。

求解步骤如下：

（1）选取 $\theta_1$，使得 $r(x|\theta_1) = p(x|\theta_1)$，然后对此时的 $r$ 求取最大值，得到极值点 $\theta_2$，实现参数的更新。

（2）重复以上过程到收敛为止，在更新过程中始终满足 $r p $.

EM算法流程

输入：观察数据 $x=(x^{(1)},x^{(2)},...x^{(m)})$，联合分布 $p(x,z ;\theta)$，条件分布 $p(z|x; \theta)$，最大迭代次数 $J$

1）随机初始化模型参数 $\theta$ 的初值 $\theta^0$。

2）$for \ j \ from \ 1 \ to \ j$：

a） E步。计算联合分布的条件概率期望：
\[ Q_i(z^{(i)}) = P( z^{(i)}|x^{(i)}, \theta^{j}) \]

\[ L(\theta, \theta^{j}) = \sum\limits_{i=1}^m\sum\limits_{z^{(i)}}P( z^{(i)}|x^{(i)}, \theta^{j})log{P(x^{(i)}, z^{(i)};\theta)} \]

b） M步。极大化 $L(\theta, \theta^{j})$，得到 $\theta^{j+1}$:
\[ \theta^{j+1} = \mathop{\arg\max}_\theta L(\theta, \theta^{j}) \]
c）如果 $\theta^{j+1}$收敛，则算法结束。否则继续回到步骤a）进行E步迭代。

输出：模型参数 $\theta$。

集成学习

集成学习的基本思想

结合多个学习器组合成一个性能更好的学习器

集成学习为什么有效

不同的模型通常会在测试集上产生不同的误差；如果成员的误差是独立的，集成模型将显著地比其成员表现更好

Boosting 方法

基于串行策略：基学习器之间存在依赖关系，新的学习器需要根据上一个学习器生成。
基本思路：
先从初始训练集训练一个基学习器；初始训练集中各样本的权重是相同的；
根据上一个基学习器的表现，调整样本权重，使分类错误的样本得到更多的关注；
基于调整后的样本分布，训练下一个基学习器；
测试时，对各基学习器加权得到最终结果
特点：
每次学习都会使用全部训练样本
代表算法：
AdaBoost 算法
GBDT 算法
XGBoost

Bagging 方法

基于并行策略：基学习器之间不存在依赖关系，可同时生成。
基本思路：
利用自助采样法对训练集随机采样，重复进行 T 次;
基于每个采样集训练一个基学习器，并得到 T 个基学习器；
预测时，集体投票决策。

自助采样法：对 m 个样本的训练集，有放回的采样 m 次；此时，样本在 m 次采样中始终没被采样的概率约为 0.368，即每次自助采样只能采样到全部样本的 63% 左右。
\[ \lim _{m \rightarrow \infty}\left(1-\frac{1}{m}\right)^{m} \rightarrow \frac{1}{e} \approx 0.368 \]
特点：
训练每个基学习器时只使用一部分样本；
偏好不稳定的学习器作为基学习器；

所谓不稳定的学习器，指的是对样本分布较为敏感的学习器。
代表方法
RF

为什么使用决策树作为基学习器

类似问题
基学习器有什么特点？
基学习器有什么要求？
使用决策树作为基学习器的原因：
决策树的表达能力和泛化能力，可以通过剪枝快速调整
决策树可以方便地将样本的权重整合到训练过程中（适合 Boosting 策略）
决策树是一种不稳定的学习器。所谓不稳定，指的是数据样本的扰动会对决策树的结果产生较大的影响。（适合 Bagging 策略）

为什么不稳定的学习器更适合作为基学习器

不稳定的学习器容易受到样本分布的影响（方差大），很好的引入了随机性；这有助于在集成学习（特别是采用 Bagging 策略）中提升模型的泛化能力
为了更好的引入随机性，有时会随机选择一个属性子集中的最优分裂属性，而不是全局最优（随机森林）

还有哪些模型也适合作为基学习器

神经网络
神经网络也属于不稳定的学习器；
此外，通过调整神经元的数量、网络层数，连接方式初始权重也能很好的引入随机性和改变模型的表达能力和泛化能力。

Boosting 方法中能使用线性分类器作为基学习器吗？ Bagging 呢？

Boosting 方法中可以使用
Boosting 方法主要通过降低偏差的方式来提升模型的性能，而线性分类器本身具有方差小的特点，所以两者有一定相性
XGBoost 中就支持以线性分类器作为基学习器。
Bagging 方法中不推荐
线性分类器都属于稳定的学习器（方差小），对数据不敏感；
甚至可能因为 Bagging 的采样，导致在训练中难以收敛，增大集成分类器的偏差

Boosting/Bagging 与偏差/方差的关系

Bagging与Dropout区别与联系

在 Bagging 的情况下，所有模型都是独立的。而在 Dropout 的情况下，所有模型共享参数，其中每个模型继承父神经网络参数的不同子集。
在 Bagging 的情况下，每一个模型都会在其相应训练集上训练到收敛。而在 Dropout 的情况下，通常大部分模型都没有显式地被训练；取而代之的是，在单个步骤中我们训练一小部分的子网络，参数共享会使得剩余的子网络也能有好的参数设定。

AdaBoost

GBDT

GBDT 是以决策树为基学习器、采用 Boosting 策略的一种集成学习模型
与提升树的区别：残差的计算不同，提升树使用的是真正的残差，梯度提升树用当前模型的负梯度来拟合残差。

RF 随机森林

XGBoost

神经网络

超参数

在机器学习的上下文中，超参数是在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。通常情况下，需要对超参数进行优化，给学习机选择一组最优超参数，以提高学习的性能和效果。

超参数具体来讲比如算法中的

学习率（learning rate）
梯度下降法迭代的数量（iterations）
隐藏层数目（hidden layers）
隐藏层单元数目
激活函数（ activation function）

都需要根据实际情况来设置，这些数字实际上控制了最后的参数和的值，所以它们被称作超参数。

如何寻找超参数的最优值

在使用机器学习算法时，总有一些难调的超参数。例如权重衰减大小，高斯核宽度等等。这些参数需要人为设置，设置的值对结果产生较大影响。常见设置超参数的方法有：

猜测和检查：根据经验或直觉，选择参数，一直迭代。
网格搜索：让计算机尝试在一定范围内均匀分布的一组值。
随机搜索：让计算机随机挑选一组值。
贝叶斯优化：使用贝叶斯优化超参数，会遇到贝叶斯优化算法本身就需要很多的参数的困难。
MITIE方法，好初始猜测的前提下进行局部优化。它使用BOBYQA算法，并有一个精心选择的起始点。由于BOBYQA只寻找最近的局部最优解，所以这个方法是否成功很大程度上取决于是否有一个好的起点。在MITIE的情况下，我们知道一个好的起点，但这不是一个普遍的解决方案，因为通常你不会知道好的起点在哪里。从好的方面来说，这种方法非常适合寻找局部最优解。稍后我会再讨论这一点。
最新提出的 LIPO 的全局优化方法。这个方法没有参数，而且经验证比随机搜索方法好。

超参数搜索一般过程

将数据集划分成训练集、验证集及测试集。
在训练集上根据模型的性能指标对模型参数进行优化。
在验证集上根据模型的性能指标对模型的超参数进行搜索。
步骤 2 和步骤 3 交替迭代，最终确定模型的参数和超参数，在测试集中验证评价模型的优劣。

其中，搜索过程需要搜索算法，一般有：网格搜索、随机搜过、启发式智能搜索、贝叶斯搜索。

梯度下降

机器学习中为什么需要梯度下降

梯度下降是迭代法的一种，可以用于求解最小二乘问题。
在求解机器学习算法的模型参数，即无约束优化问题时，主要有梯度下降法（Gradient Descent）和最小二乘法。
在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。
如果我们需要求解损失函数的最大值，可通过梯度上升法来迭代。梯度下降法和梯度上升法可相互转换。
在机器学习中，梯度下降法主要有随机梯度下降法和批量梯度下降法。

梯度下降法缺点

靠近极小值时收敛速度减慢。
直线搜索时可能会产生一些问题。
可能会“之字形”地下降。

梯度概念需注意：

梯度是一个向量，即有方向有大小。
梯度的方向是最大方向导数的方向。
梯度的值是最大方向导数的值。

梯度下降法直观理解

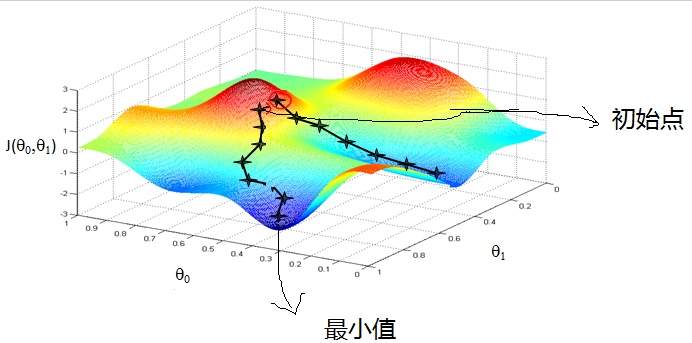
形象化举例，由上图，假如最开始，我们在一座大山上的某处位置，因为到处都是陌生的，不知道下山的路，所以只能摸索着根据直觉，走一步算一步，在此过程中，每走到一个位置的时候，都会求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。不断循环求梯度，就这样一步步地走下去，一直走到我们觉得已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山势低处。
由此，从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部的最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

初始化参数，随机选取取值范围内的任意数；
迭代操作：
a）计算当前梯度；
b）修改新的变量；
c）计算朝最陡的下坡方向走一步；
d）判断是否需要终止，如否，返回a）；
得到全局最优解或者接近全局最优解。

梯度下降法算法描述

1 . 确定优化模型的假设函数
举例，对于线性回归，假设函数为：
\[ h_\theta(x_1,x_2,...,x_n)=\theta_0+\theta_1x_1+...+\theta_nx_n \]
其中，$\theta_j,x_j(j=0,1,2,...,n)$分别为模型参数、每个样本的特征值。
2 . 损失函数
\[ J(\theta_0,\theta_1,...,\theta_n)=\frac{1}{2m}\sum^{m}_{i=0}(h_\theta (x^{(i)})-y^{(i)})^2 \]
3 . 相关参数初始化
主要初始化 ${\theta}_j$、算法迭代步长 ${} $、终止距离 ${} $。初始化时可以根据经验初始化，即 ${\theta}$ 初始化为0，步长 ${\alpha}$ 初始化为1。当前步长记为 ${\varphi}_j$。当然，也可随机初始化。

4 . 迭代计算

1）计算当前位置时损失函数的梯度，对 ${}_j $，其梯度表示为：
\[ \frac{\partial}{\partial \theta_j}J({\theta}_0,{\theta}_1,...,{\theta}_n)=\frac{1}{2m}\sum^{m}_{i=0}(h_\theta (x^{(i)})-y^{(i)})^2 \]
2）计算当前位置下降的距离。
\[ {\varphi}_j={\alpha} \frac{\partial}{\partial \theta_j}J({\theta}_0,{\theta}_1,...,{\theta}_n) \]
3）判断是否终止

确定是否所有 ${\theta}_j$ 梯度下降的距离 ${\varphi}_j$ 都小于终止距离 ${\zeta}$，如果都小于 ${\zeta}$，则算法终止，当然的值即为最终结果，否则进入下一步。

4）更新所有的 ${\theta}_j$，更新后的表达式为
\[ \begin{aligned} {\theta}_j & ={\theta}_j-\alpha \frac{\partial}{\partial \theta_j}J({\theta}_0,{\theta}_1,...,{\theta}_n) \\ & =\theta_j - \alpha \frac{1}{m} \sum^{m}_{i=0}(h_\theta (x^{(i)}-y^{(i)})x^{(i)}_j) \end{aligned} \]
5）令上式 $x^{(i)}_0=1$，更新完毕后转入 1)
由此，可看出，当前位置的梯度方向由所有样本决定，上式中 $\frac{1}{m}$、$\alpha \frac{1}{m}$ 的目的是为了便于理解。

如何对梯度下降法进行调优

实际使用梯度下降法时，各项参数指标不能一步就达到理想状态，对梯度下降法调优主要体现在以下几个方面：

算法迭代步长 $\alpha$ 选择。
在算法参数初始化时，有时根据经验将步长初始化为1。实际取值取决于数据样本。可以从大到小，多取一些值，分别运行算法看迭代效果，如果损失函数在变小，则取值有效。如果取值无效，说明要增大步长。但步长太大，有时会导致迭代速度过快，错过最优解。步长太小，迭代速度慢，算法运行时间长。
参数的初始值选择。
初始值不同，获得的最小值也有可能不同，梯度下降有可能得到的是局部最小值。如果损失函数是凸函数，则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。
标准化处理。
由于样本不同，特征取值范围也不同，导致迭代速度慢。为了减少特征取值的影响，可对特征数据标准化，使新期望为0，新方差为1，可节省算法运行时间。

随机梯度和批量梯度区别

随机梯度下降（SGD）

其每次迭代，只用一个训练数据来更新 $\theta$ ，即代价函数对参数的偏导数为：
\[ \begin{aligned} {\alpha} \frac{\partial}{\partial \theta_j}J({\theta}_0,{\theta}_1,...,{\theta}_n) & = \frac{\partial}{\partial \theta_j} [\frac{1}{2}(h_{\theta}(x) - y)^2] \\ & = 2 \cdot \frac{1}{2}(h_{\theta}(x) - y) \cdot \frac{\partial}{\partial \theta_j} (h_{\theta}(x) - y) \\ & = (h_{\theta}(x) - y)\cdot x_j \end{aligned} \]
即此时的参数更新为：
\[ {\theta}_j =\theta_j - \alpha \frac{1}{m} (h_\theta (x^{(i)}-y^{(i)})x^{(i)}_j) \]

批量梯度下降（BGD）

每次迭代，使用所有的数据来更新 $\theta$ ，此时代价函数对参数的偏导数为：
\[ \begin{aligned} {\alpha} \frac{\partial}{\partial \theta_j}J({\theta}_0,{\theta}_1,...,{\theta}_n) & = \frac{\partial}{\partial \theta_j} [\frac{1}{2m}\sum_{i = 1}^{m}(h_{\theta}(x^{(i)}) -y^{(i)})^2] \\ & = \frac{1}{m} \sum_{i = 1}^{m}(h_{\theta}(x^{(i)}) -y^{(i)})\cdot x_j^{(i)} \end{aligned} \\ \]
即此时的参数更新为：
\[ {\theta}_j =\theta_j - \alpha \frac{1}{m} \sum_{i = 1}^{m} (h_\theta (x^{(i)}-y^{(i)})x^{(i)}_j) \]
小结：随机梯度下降法、批量梯度下降法相对来说都比较极端，简单对比如下：

方法	特点
批量梯度下降	a）采用所有数据来梯度下降。 b）批量梯度下降法在样本量很大的时候，训练速度慢。
随机梯度下降	a）随机梯度下降用一个样本来梯度下降。 b）训练速度很快。 c）随机梯度下降法仅仅用一个样本决定梯度方向，导致解有可能不是全局最优。 d）收敛速度来说，随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

下面介绍能结合两种方法优点的小批量梯度下降法。

小批量梯度下降（Mini-batch GD）

对于总数为 $m$ 个样本的数据，根据样本的数据，选取其中的$n(1< n< m)$个子样本来迭代。其参数 $\theta$ 按梯度方向更新 $\theta_j$ 公式如下：
\[ {\theta}_j =\theta_j - \alpha \frac{1}{m} \sum_{i = t}^{t+n-1} (h_\theta (x^{(i)}-y^{(i)})x^{(i)}_j) \]

各种梯度下降法性能比较

下表简单对比 随机梯度下降（SGD）、批量梯度下降（BGD）、小批量梯度下降（Mini-batch GD）、和 Online GD 的区别：

	BGD	SGD	Mini-batch GD	Online GD
训练集	固定	固定	固定	实时更新
单次迭代样本数	整个训练集	单个样本	训练集的子集	根据具体算法定
算法复杂度	高	低	一般	低
时效性	低	一般	一般	高
收敛性	稳定	不稳定	较稳定	不稳定

BGD、SGD、Mini-batch GD，前面均已讨论过，这里介绍一下Online GD

Online GD 与Mini-batch GD/SGD的区别在于，所有训练数据只用一次，然后丢弃。这样做的优点在于可预测最终模型的变化趋势。

Online GD在互联网领域用的较多，比如搜索广告的点击率（CTR）预估模型，网民的点击行为会随着时间改变。用普通的BGD算法（每天更新一次）一方面耗时较长（需要对所有历史数据重新训练）；另一方面，无法及时反馈用户的点击行为迁移。而Online GD算法可以实时的依据网民的点击行为进行迁移。

梯度爆炸与梯度消失

梯度消失 / 梯度爆炸

在深层网络中，由于网络过深，如果初始得到的梯度过小，或者传播途中在某一层上过小，则在之后的层上得到的梯度会越来越小，即产生了梯度消失。梯度爆炸也是同样的。一般地，不合理的权值初始化（过大或过小）以及激活函数，如 $Sigmoid$ 等，都会导致梯度过大或者过小，从而引起消失/爆炸。

（1）网络深度

若在网络很深时，若权重初始化较小，各层上的相乘得到的数值都会0-1之间的小数，而激活函数梯度也是0-1之间的数。那么连乘后，结果数值就会变得非常小，导致梯度消失。若权重初始化较大，大到乘以激活函数的导数都大于1，那么连乘后，可能会导致求导的结果很大，形成梯度爆炸。

（2）激活函数
如果激活函数选择不合适，比如使用 $Sigmoid$，就很容易导致梯度消失。$Sigmoid$ 函数，在输入取绝对值非常大的正值或负值时会出现饱和现象，梯度趋于0，并且 $Sigmoid$ 函数的梯度在 $(0, \frac{1}{4}]$ ，这样经过链式求导之后，很容易发生梯度消失。

梯度消失、爆炸的解决方案

梯度剪切、正则

梯度剪切这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
另外一种解决梯度爆炸的手段是采用权重正则化（weithts regularization）比较常见的是L1和L2正则。

使用 $ReLu、Leaky \ ReLu$ 等激活函数

$ReLU$ 的导数始终是一个常数，负半区为 0，正半区为 1，所以不会发生梯度消失现象。$Leaky \ ReLU$ 则是为了解决 $ReLU$ 神经元 Dead 现象，在 $x < 0$ 时，取 $0.1x$

使用 BN

BN 方法会针对每一批数据，在网络的每一层输入之前增加归一化处理，使输入的均值为 0，标准差为 1。目的是将数据限制在统一的分布下，保证网络的稳定性。然后再引入一个重构变换，还原最优的原始输入分布，做为神经元的激活值，该方法可以很好的缓解梯度消失问题。

残差结构

残差的方式，能使得深层的网络梯度通过跳级连接路径直接返回到浅层部分，使得网络无论多深都能将梯度进行有效的回传。

LSTM

LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原因在于LSTM内部复杂的“门”(gates)。在计算时，将过程中的梯度进行了抵消。

深度学习为什么要使用梯度更新规则

深度学习中的反向传播，即根据损失函数计算的误差，计算得到梯度，通过梯度反向传播的方式，指导深度网络权值的更新优化。这样做的原因在于，深层网络由许多非线性层堆叠而来，每一层非线性层都可以视为是一个非线性函数，因此整个深度网络可以视为是一个复合的非线性多元函数：
\[ F(x)=f_n(\cdots f_3(f_2(f_1(x)*\theta_1+b)*\theta_2+b)\cdots) \]
我们最终的目的是希望这个多元函数可以很好的完成输入到输出之间的映射，假设不同的输入，输出的最优解是g(x) ，那么，优化深度网络就是为了寻找到合适的权值，满足 $Loss=L(g(x),F(x))$ 取得极小值点，比如最简单的损失函数：
\[ Loss = \lVert g(x)-f(x) \rVert^2_2. \]
假设损失函数的数据空间是下图这样的，我们最优的权值就是为了寻找下图中的最小值点，对于这种数学寻找最小值问题，采用梯度下降的方法再适合不过了。

如何防止梯度下降陷入局部最优解

Mini-Batch SGD
SGD-M
自适应学习率
Adagrad
RMSprop
Adam

梯度下降与正规方程的比较

梯度下降(Gradient Descent)	正规方程(Normal Equation)
需要选择学习率	不需要
需要多次迭代	一次运算得出
当特征数量 n 大时，也能较好适用	需要计算如果特征数量 n 较大则运算代价大，因为矩阵逆的计算时间复杂度为，通常来说当n小于10000时还是可以接受的
适用于各种类型的模型	只适用于线性模型，不适合逻辑回归等其他模型

最小二乘法和梯度下降法区别

最小二乘法的目标：求误差的最小平方和，对应有两种：线性和非线性。线性最小二乘的解是closed-form即$x=\left(A^{T} A\right)^{-1} A^{T} b$，而非线性最小二乘没有closed-form，通常用迭代法求解。

迭代法，即在每一步update未知量逐渐逼近解，可以用于各种各样的问题（包括最小二乘），比如求的不是误差的最小平方和而是最小立方和。

梯度下降是迭代法的一种，可以用于求解最小二乘问题（线性和非线性都可以）。高斯-牛顿法是另一种经常用于求解非线性最小二乘的迭代法（一定程度上可视为标准非线性最小二乘求解方法）。

所以如果把最小二乘看做是优化问题的话，那么梯度下降是求解方法的一种，$x=\left(A^{T} A\right)^{-1} A^{T} b$ 是求解线性最小二乘的一种，高斯-牛顿法和Levenberg-Marquardt则能用于求解非线性最小二乘。

基于二阶梯度的优化算法

牛顿法

梯度下降使用的梯度信息实际上是一阶导数
牛顿法除了一阶导数外，还会使用二阶导数的信息
根据导数的定义，一阶导描述的是函数值的变化率，即斜率；二阶导描述的则是斜率的变化率，即曲线的弯曲程度——曲率

数学/泰勒级数

牛顿法更新过程 TODO

《统计学习方法》附录 B

为什么牛顿法比梯度下降收敛更快？

常见的几种最优化方法（梯度下降法、牛顿法、拟牛顿法、共轭梯度法等） - 蓝鲸王子 - 博客园

几何理解

牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面；而梯度下降法是用一个平面去拟合当前的局部曲面。
通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

通俗理解

比如你想找一条最短的路径走到一个盆地的最底部，
梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步；
牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。
所以，牛顿法比梯度下降法看得更远，能更快地走到最底部。

牛顿法的优缺点

优点
收敛速度快，能用更少的迭代次数找到最优解
缺点
每一步都需要求解目标函数的 Hessian 矩阵的逆矩阵，计算复杂

Hessian 矩阵即由二阶偏导数构成的方阵

拟牛顿法 TODO

用其他近似方法代替求解 Hessian 矩阵的逆矩阵

梯度检验

思想：是通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。

对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的 $θ$，我们计算出在 $θ-ε$ 处和 $θ+ε$ 的代价值（ ε 是一个非常小的值，通常选取 0.001），然后求两个代价的平均，用以估计在 $θ$ 处的代价值。

当 $θ$ 是一个向量时，我们则需要对偏导数进行检验。因为代价函数的偏导数检验只针对一个参数的改变进行检验，下面是一个只针对 $θ_1$ 进行检验的示例：
\[ \frac{\partial}{\partial \theta_{I}}=\frac{J\left(\theta_{I}+\varepsilon_{l}, \theta_{2}, \theta_{3} \dots \theta_{n}\right)-J\left(\theta_{I}-\varepsilon_{l}, \theta_{2}, \theta_{3} \dots \theta_{n}\right)}{2 \varepsilon} \]
最后我们还需要对通过反向传播方法计算出的偏导数进行检验。

根据上面的算法，计算出的偏导数存储在矩阵 $D^{(l)}_{ij}$ 中。检验时，我们要将该矩阵展开成为向量，同时我们也将 $θ$ 矩阵展开为向量，我们针对每一个 $θ$ 都计算一个近似的梯度值，将这些值存储于一个近似梯度矩阵中，最终将得出的这个矩阵同 $D^{(l)}_{ij}$ 进行比较。

batch_size

为什么需要 batch_size

batch 的选择，首先决定的是下降的方向。

如果数据集比较小，可采用全数据集的形式，好处是：由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。但由于不同权重的梯度值差别巨大，因此选取一个全局的学习率很困难。随着数据集的海量增长和内存限制，一次性载入所有的数据进来变得越来越不可行。

而 batch_size = 1 时为随机梯度下降，每次只用一个训练数据来更新参数，导致迭代方向变化很大，不能很快的收敛到局部最优解。

所以可以采用 batch_size 批量的进行训练。

在合理范围内，增大Batch_Size有何好处

内存利用率提高了，大矩阵乘法的并行化效率提高。
跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
在一定范围内，一般来说 batch_size 越大，其确定的下降方向越准，引起训练震荡越小。

盲目增大 Batch_Size 有何坏处

batch_size 太小，模型表现效果极其糟糕(error飙升)。
随着 batch_size 增大，处理相同数据量的速度越快。
随着 batch_size 增大，达到相同精度所需要的 epoch 数量越来越多。
由于上述两种因素的矛盾， batch_size 增大到某个时候，达到时间上的最优。
由于最终收敛精度会陷入不同的局部极值，因此 batch_size 增大到某些时候，达到最终收敛精度上的最优。

学习率 learning rate

数据处理

类别不平衡问题

对多的那个类别进行欠采样(under-sampling)，舍弃一部分数据，使其与较少类别的数据相当（代表方法：Easy Ensemble）

Easy Ensemble：结合集成学习来有效的使用数据，假设正例数为少数 n，而反例数据多为 m 个。我们可以通过欠采样，随机无重复的生成（k=m/n）个反例子集，并将每个子集都与相同正例数据合并生成 k 个新的训练样本。我们在 k 个训练样本上分别训练一个分类器，预测时，将 k 个分类器进行集体投票表决

对较少的类别进行过采样(over-sampling)，重复使用一部分数据，使其与较多类别的数据相当（代表方法：SMOTE）

SMOTE：通过对训练集里的较少的类别进行插值来产生而外的的数据

阈值调整（threshold moving），将原本默认为0.5的阈值调整到 较少类别 / (较少类别+较多类别) 即可

处理数据中的缺失值

可以分为以下 2 种情况：

缺失值较多

直接舍弃该列特征，否则可能会带来较大的噪声，从而对结果造成不良影响。

缺失值较少

当缺失值较少（<10%）时，可以考虑对缺失值进行填充，以下是几种常用的填充策略：

用一个异常值填充（比如 0），将缺失值作为一个特征处理data.fillna(0)
用均值|条件均值填充 data.fillna(data.mean())

如果数据是不平衡的，那么应该使用条件均值填充。所谓条件均值，指的是与缺失值所属标签相同的所有数据的均值

用相邻数据填充

# 用前一个数据填充
data.fillna(method='pad')
# 用后一个数据填充
data.fillna(method='bfill')

插值 data.interpolate()
拟合

简单来说，就是将缺失值也作为一个预测问题来处理：将数据分为正常数据和缺失数据，对有值的数据采用随机森林等方法拟合，然后对有缺失值的数据进行预测，用预测的值来填充。

训练样本少的问题

（1）利用预训练模型进行迁移微调（fine-tuning）

（2）数据集增强

（3）正则化

（4）单样本或者少样本学习（one-shot，few-shot learning）

（5）半监督学习

数据增强方法

Color Jittering：对颜色的数据增强：图像亮度、饱和度、对比度变化（此处对色彩抖动的理解不知是否得当）
PCA Jittering：首先按照RGB三个颜色通道计算均值和标准差，再在整个训练集上计算协方差矩阵，进行特征分解，得到特征向量和特征值，用来做PCA Jittering；
Random Scale：尺度变换
Random Crop：采用随机图像差值方式，对图像进行裁剪、缩放；包括 Scale Jittering 方法（VGG及ResNet模型使用）或者尺度和长宽比增强变换
Horizontal/Vertical Flip：水平/垂直翻转；
Shift：平移变换
Rotation/Reflection：旋转/仿射变换；
Noise：高斯噪声、模糊处理
Label Shuffle：类别不平衡数据的增广

权值初始化方法

在深度学习的模型中，从零开始训练时，权重的初始化有时候会对模型训练产生较大的影响。良好的初始化能让模型快速、有效的收敛，而糟糕的初始化会使得模型无法训练。

目前，大部分深度学习框架都提供了各类初始化方式，其中一般常用的会有如下几种：

常数初始化(constant)

把权值或者偏置初始化为一个常数。例如设置为0，偏置初始化为0较为常见，权重很少会初始化为0。TensorFlow中也有zeros_initializer、ones_initializer等特殊常数初始化函数。

高斯初始化(gaussian)

给定一组均值和标准差，随机初始化的参数会满足给定均值和标准差的高斯分布。高斯初始化是很常用的初始化方式。特殊地，在TensorFlow中还有一种截断高斯分布初始化（truncated_normal_initializer），其主要为了将超过两个标准差的随机数重新随机，使得随机数更稳定。

均匀分布初始化(uniform)

给定最大最小的上下限，参数会在该范围内以均匀分布方式进行初始化，常用上下限为（0，1）。

xavier 初始化(uniform)

在batchnorm还未出现之前，要训练较深的网络，防止梯度弥散，需要依赖非常好的初始化方式。xavier 就是一种比较优秀的初始化方式，也是目前最常用的初始化方式之一。其目的是为了使得模型各层的激活值和梯度在传播过程中的方差保持一致。本质上xavier 还是属于均匀分布初始化，但与上述的均匀分布初始化有所不同，xavier 的上下限将在如下范围内进行均匀分布采样：
\[ [-\sqrt{\frac{6}{n+m}},\sqrt{\frac{6}{n+m}}] \]
其中，n为所在层的输入维度，m为所在层的输出维度。

kaiming初始化（msra 初始化）

kaiming初始化，在caffe中也叫msra 初始化。kaiming初始化和xavier 一样都是为了防止梯度弥散而使用的初始化方式。kaiming初始化的出现是因为xavier存在一个不成立的假设。xavier在推导中假设激活函数都是线性的，而在深度学习中常用的ReLu等都是非线性的激活函数。而kaiming初始化本质上是高斯分布初始化，与上述高斯分布初始化有所不同，其是个满足均值为0，方差为2/n的高斯分布：
\[ [0,\sqrt{\frac{2}{n}}] \\ （其中，n为所在层的输入维度） \]
除上述常见的初始化方式以外，不同深度学习框架下也会有不同的初始化方式，读者可自行查阅官方文档。

深度学习是否能胜任所有数据集

深度学习并不能胜任目前所有的数据环境，以下列举两种情况：

（1）深度学习能取得目前的成果，很大一部分原因依赖于海量的数据集以及高性能密集计算硬件。因此，当数据集过小时，需要考虑与传统机器学习相比，是否在性能和硬件资源效率更具有优势。

（2）深度学习目前在视觉，自然语言处理等领域都有取得不错的成果。这些领域最大的特点就是具有局部相关性。例如图像中，人的耳朵位于两侧，鼻子位于两眼之间，文本中单词组成句子。这些都是具有局部相关性的，一旦被打乱则会破坏语义或者有不同的语义。所以当数据不具备这种相关性的时候，深度学习就很难取得效果。

共线性，如何判断和解决共线性问题

对于回归算法，无论是一般回归还是逻辑回归，在使用多个变量进行预测分析时，都可能存在多变量相关的情况，这就是多重共线性。共线性的存在，使得特征之间存在冗余，导致过拟合。
常用判断是否存在共线性的方法有：

（1）相关性分析。当相关性系数高于0.8，表明存在多重共线性；但相关系数低，并不能表示不存在多重共线性；

（2）方差膨胀因子VIF。当VIF大于5或10时，代表模型存在严重的共线性问题；

（3）条件系数检验。当条件数大于100、1000时，代表模型存在严重的共线性问题。

通常可通过PCA降维、逐步回归法和LASSO回归等方法消除共线性。

Ones-Hot 编码

很多机器学习任务中，特征并不总是连续值，有可能是分类值。
考虑以下三个特征：

[“male”, “female”][“from Europe”, “from US”, “from Asia”]
[“uses Firefox”, “uses Chrome”, “uses Safari”, “uses Internet Explorer”]

如果将上述特征用数字表示，效率会高很多。例如：

[“male”, “from US”, “uses Internet Explorer”] 表示为[0, 1, 3][“female”, “from Asia”, “uses Chrome”]表示为[1, 2, 1]

但是，转化为数字表示后，上述数据不能直接用在我们的分类器中。因为，分类器往往默认数据数据是连续的，并且是有序的。但按上述表示的数字并不有序的，而是随机分配的。

One-Hot Encoding 独热编码，又称一位有效编码，其方法是使用 N 位状态寄存器来对 N 个状态进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。

自然状态码为：000,001,010,011,100,101
独热编码为：000001,000010,000100,001000,010000,100000

可以这样理解，对于每一个特征，如果它有m个可能值，那么经过独热编码后，就变成了m个二元特征。并且，这些特征互斥，每次只有一个激活。因此，数据会变成稀疏的。

这样做的好处主要有：

解决了分类器不好处理属性数据的问题
在一定程度上也起到了扩充特征的作用

例子

encoder = preprocessing.OneHotEncoder()
encoder.fit([
    [0, 2, 1, 12],
    [1, 3, 5, 3],
    [2, 3, 2, 12],
    [1, 2, 4, 3]
])
encoded_vector = encoder.transform([[2, 3, 5, 3]]).toarray()
print("\n Encoded vector =", encoded_vector)

# 输出结果
Encoded vector = [[ 0. 0. 1. 0. 1. 0. 0. 0. 1. 1. 0.]]

分析

4个特征：
第一个特征（即为第一列）为[0,1,2,1] ，其中三类特征值[0,1,2]，因此One-Hot Code可将[0,1,2]表示为:[100,010,001]
同理第二个特征列可将两类特征值[2,3]表示为[10,01]
第三个特征将4类特征值[1,2,4,5]表示为[1000,0100,0010,0001]
第四个特征将2类特征值[3,12]表示为[10,01]

因此最后可将[2,3,5,3]表示为[0,0,1,0,1,0,0,0,1,1,0]

特征选择(feature selection)

特征类型有哪些

对象本身会有许多属性。所谓特征，即能在某方面最能表征对象的一个或者一组属性。一般地，我们可以把特征分为如下三个类型：

（1）相关特征：对于特定的任务和场景具有一定帮助的属性，这些属性通常能有效提升算法性能；

（2）无关特征：在特定的任务和场景下完全无用的属性，这些属性对对象在本目标环境下完全无用；

（3）冗余特征：同样是在特定的任务和场景下具有一定帮助的属性，但这类属性已过多的存在，不具有产生任何新的信息的能力。

如何考虑特征选择

当完成数据预处理之后，对特定的场景和目标而言很多维度上的特征都是不具有任何判别或者表征能力的，所以需要对数据在维度上进行筛选。一般地，可以从以下两个方面考虑来选择特征:

（1）特征是否具有发散性：某个特征若在所有样本上的都是一样的或者接近一致，即方差非常小。也就是说所有样本的都具有一致的表现，那这些就不具有任何信息。

（2）特征与目标的相关性：与目标相关性高的特征，应当优先选择。

特征选择方法分类

根据特征选择的形式又可以将特征选择方法分为 3 种:
（1）过滤法：按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。

（2）包装法：根据目标函数(通常是预测效果评分)，每次选择若干特征，或者排除若干特征。

（3）嵌入法：先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。

特征选择目的

（1）减少特征维度，使模型泛化能力更强，减少过拟合;

（2）降低任务目标的学习难度；

（3）一组优秀的特征通常能有效的降低模型复杂度，提升模型效率

归一化与标准化

归一化和标准化本质上都是一种线性变换

（1）归一化

１）把数据把数据映射到 0～1 范围之内处理，更加便捷，可以加快梯度下降求解速度，提升模收敛速度。消除了量纲，便于不同单位或量级的指标能够进行比较和加权。
\[ \frac{x - min}{max-min} \]
（2）标准化

对数据减去均值，除以标准差，转换为标准正太分布（均值为0，标准差为1），和整体样本分布相关，每个样本都能对标准化产生影响。
\[ \frac{x - \mu}{\sigma} \]
其中 $\mu$ 和 $\sigma$ 代表样本的均值和标准差。

（3）两者的异同

归一化：缩放仅仅跟最大、最小值的差别有关。
标准化：缩放和每个点都有关系，通过方差（variance）体现出来。与归一化对比，标准化中所有数据点都有贡献（通过均值和标准差造成影响）。

（4）如何选择

如果对输出结果范围有要求，用归一化
如果数据较为稳定，不存在极端的最大最小值，用归一化
如果数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响

Batch Normalization(批标准化)

BN层作用，以及如何使用BN层

BN (Batch Normalization批标准化) 是一种正则化方法（减少泛化误差），主要作用有：

加速网络的训练
缓解梯度消失
防止过拟合
增强模型的泛化能力
支持更大的学习率
降低了参数初始化的要求

动机

训练的本质是学习数据分布。如果训练数据与测试数据的分布不同会降低模型的泛化能力。因此，应该在开始训练前对所有输入数据做归一化处理。
而在神经网络中，因为每个隐层的参数不同，会使下一层的输入发生变化，从而导致每一批数据的分布也发生改变；致使网络在每次迭代中都需要拟合不同的数据分布，增大了网络的训练难度与过拟合的风险。

基本原理

（1）训练阶段

BN 方法会针对每一批数据，在网络的每一层输入之前增加归一化处理，使输入的均值为 0，标准差为 1。目的是将数据限制在统一的分布下。
具体来说，针对每层的第 k 个神经元，计算这一批数据在第 k 个神经元的均值与标准差，然后将归一化后的值作为该神经元的激活值。

\[ \boldsymbol{\hat{x}_{k}} = \frac{\boldsymbol{x_{k}}-\mathrm{E}\left[\boldsymbol{x_{k}}\right]}{\sqrt{\operatorname{Var}\left[\boldsymbol{x_{k}}\right]}} \]

BN 可以看作在各层之间加入了一个新的计算层，对数据分布进行额外的约束，从而增强模型的泛化能力；
但同时 BN 也降低了模型的拟合能力，破坏了之前学到的特征分布；
为了恢复数据的原始分布，BN 引入了一个重构变换来还原最优的输入数据分布，其中 γ 和 β 是我们要训练学习的参数。

\[ \boldsymbol{y_{k}} \leftarrow \gamma \boldsymbol{\hat{x}_{k}}+\beta \]

小结：

以上过程可归纳为一个 BN(x) 函数：

\[ \large\begin{aligned} \large\boldsymbol{y_i}= \mathrm{BN}(\boldsymbol{x_i}) &=\gamma\boldsymbol{\hat{x}_i} + \beta \\ &=\gamma\frac{\boldsymbol{x_i}-\boldsymbol{\mathrm{E}[x_i]}}{\sqrt{\boldsymbol{\mathrm{Var}[x_i]}+\epsilon}}+\beta\end{aligned} \]

完整算法：

输入：上一层输出结果 $ = x_1, x_2, … , x_m$ ，学习参数 $\gamma, \beta$
算法流程：

计算上一层输出数据的均值

\[ \mu_{\mathcal{B}} = \frac{1}{m} \sum_{i=1}^m(x_i) \]

（其中，m是此次训练样本 batch 的大小）

计算上一层输出数据的标准差

\[ \sigma_{\mathcal{B}}^2 = \frac{1}{m} \sum_{i=1}^m (x_i - \mu_{\mathcal{B}})^2 \]

归一化处理，目的是为了将数据限制在统一的分布之下

\[ \hat x_i = \frac{x_i - \mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^2 + \epsilon}} \]

（其中 $ $ 是为了避免分母为 0 而加进去的接近于 0 的很小值）

重构，对经过上面归一化处理得到的数据进行重构，还原最优的输入数据分布，作为该层神经元的激活值
\[ y_i = \gamma \hat x_i + \beta \]
（其中，$ , $ 为可学习参数）

（2）测试阶段

测试的时候，每次可能只会传入单个数据，此时的均值和标准差，模型会使用全局统计量代替批统计量；即使用训练时所有batch得到的一组组的均值和方差，计算其数学期望做为全局统计量。
\[ \begin{array}{c}{\mathrm{E}[x] \leftarrow \mathrm{E}\left[\mu_{i}\right]} \\ {\operatorname{Var}[x] \leftarrow \frac{m}{m-1} \mathrm{E}\left[\sigma_{i}^{2}\right]}\end{array} \]

其中 $μ_i$ 和 $σ_i$ 分别表示第 $i$ 轮 batch 保存的均值和标准差；$m$ 为 batch_size，系数 $\frac{m}{m-1}$ 用于计算无偏方差估计 （原文称该方法为移动平均（moving averages））

然后再将按照训练的流程，将输入数据，减去全局统计量均值除以标准差，再进行重构变换得到新的数据作为神经元的激活值。

此时，BN(x) 调整为：

\[ \large\begin{aligned}\mathrm{BN}(\boldsymbol{x_i})&=\gamma\frac{\boldsymbol{x_i}-\boldsymbol{\mathrm{E}[x_i]}}{\sqrt{\boldsymbol{\mathrm{Var}[x_i]} + \epsilon}} + \beta\\&=\frac{\gamma}{\sqrt{\boldsymbol{\mathrm{Var}[x_i]} + \epsilon}}\boldsymbol{x_i} + \left(\beta-\frac{\gamma\boldsymbol{\mathrm{E}[x_i]}}{\sqrt{\boldsymbol{\mathrm{Var}[x_i]} + \epsilon}}\right)\end{aligned} \]

这样写的目的是为了减少计算量，推理阶段公式中的两个分式是固定值，可以预先计算好，这样推理阶段就可以直接使用。

完整算法：

Reference: 理解源码解读实战知乎

为什么训练时不采用移动平均？

用 BN 的目的就是为了保证每批数据的分布稳定，使用训练时使用全局统计量反而违背了这个初衷
BN 的作者认为在训练时采用移动平均可能会与梯度优化存在冲突

BN、LN、IN、GN的异同

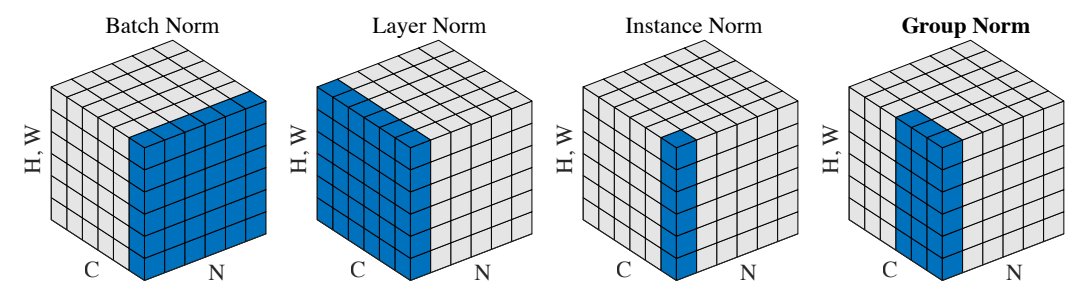
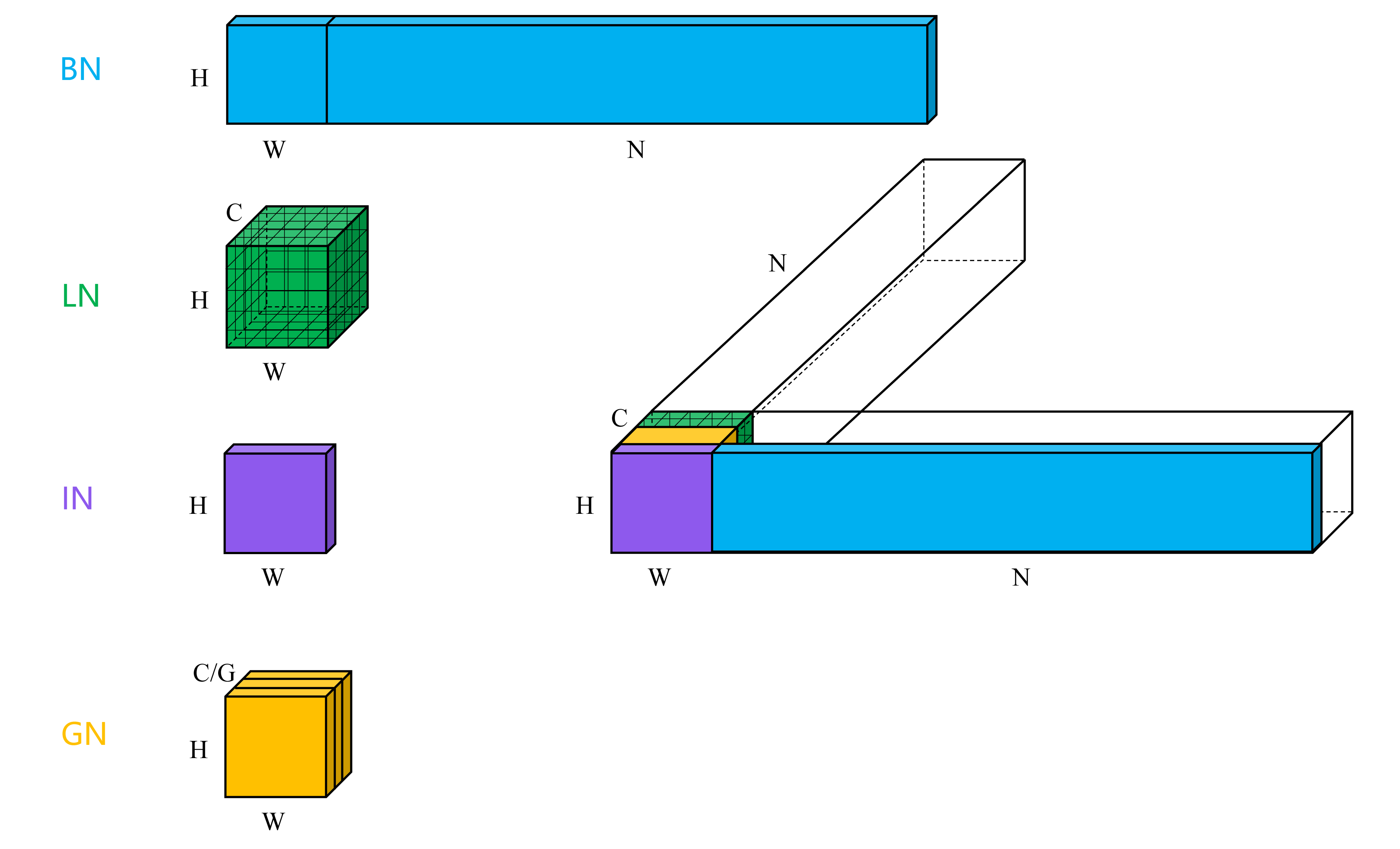
深度网络中的数据维度一般为：[N, C, H, W] 或者[N, H, W, C]格式，分别对应上图两种排列方式。

其中：

N ：batch_size
W ：feature map 的宽
H ：feature map 的高
C ：feature map 的通道数

BN： 在batch的维度上进行norm，归一化维度为 [N, H, W]，BN对batch size有依赖，当batch size较大时，有不错的效果。而 LN、IN、GN 能够摆脱这种依赖，其中GN效果最好。

LN： 避开了batch维度，归一化的维度为 [C，H，W]

IN： 归一化维度为 [H, W]

GN： GN 介于 LN 和 IN 之间，其首先将channel分为许多组（group），对每一组做归一化，即先将feature的维度由[N, C, H, W] reshape为 [N*G，C//G , H, W]，归一化的维度为 [C//G , H, W] 。GN相当于特征的group归一化，其对batch_size更鲁棒

事实上，GN 的极端情况就是 LN 和 IN，分别对应G等于1和G等于C

Dropout

Reference

Dropout是指在网络的训练过程中，每份小批量训练数据集，以一定的概率随机地 “临时丢弃”一部分神经元节点，相当于每次迭代都在训练不同结构的神经网络，相当于Bagging的近似集成。对于任意神经元，每次训练中都与一组随机挑选的不同的神经元集合共同进行优化，这个过程会减弱全体神经元之间的联合适应性，减少过拟合的风险，增强泛化能力。

但与Bagging不同的是：

Bagging涉及多个模型的同时训练与测试评估，当网络与参数规模庞大时，这种集成方式需要消耗大量的运算时间与空间。 Dropout在小批量级别上的操作，提供了一种轻量级的Bagging集成近似，能够实现指数级数量神经网络的训练与评测。
Bagging训练所有的模型都是独立的，而在 Dropout 的情况下，所有模型共享参数，其中每个模型继承父神经网络参数的不同子集。

利用自助采样法对训练集随机采样，重复进行 T 次;

基于每个采样集训练一个基学习器，并得到 T 个基学习器；

预测时，集体投票决策。

在 Bagging 的情况下，每一个模型都会在其相应训练集上训练到收敛。而在 Dropout 的情况下，通常大部分模型都没有显式地被训练；取而代之的是，在单个步骤中我们训练一小部分的子网络，参数共享会使得剩余的子网络也能有较好的参数设定。

Dropout 具体实现

(1) 训练时，每个神经元节点需要增加一个概率系数：

没有Dropout的网络计算公式：

\[ \begin{aligned} z_{i}^{(l+1)} &=\mathrm{w}_{i}^{(l+1)} \mathrm{y}^{l}+b_{i}^{(l+1)} \\ y_{i}^{(l+1)} &=f\left(z_{i}^{(l+1)}\right) \end{aligned} \]

采用Dropout的网络计算公式：

\[ \begin{aligned} r_{j}^{(l)} & \sim \text { Bernoulli }(p) \\ \widetilde{\mathbf{y}}^{(l)} &=\mathbf{r}^{(l)} * \mathbf{y}^{(l)} \\ z_{i}^{(l+1)} &=\mathbf{w}_{i}^{(l+1)} \widetilde{\mathbf{y}}^{l}+b_{i}^{(l+1)} \\ y_{i}^{(l+1)} &=f\left(z_{i}^{(l+1)}\right) \end{aligned} \]

Bernoulli函数的作用是以概率系数 $p$ 随机生成一个取值为0或1的向量，代表每个神经元是否需要被丢弃。如果取值为 0，则该神经元将不会计算梯度或参与后面的误差传播。

(2) 测试时，每一个神经单元的权重参数要乘以概率 $p$，以恢复在训练中该神经元只有 $p$ 的概率被用于整个神经网络的前向传播计算。
\[ w_{t e s t}^{(l)}=p W^{(l)} \]

Dropput 为何能解决过拟合？

对于任意神经元，每次训练中都与一组随机挑选的不同的神经元集合共同进行优化，这个过程会减弱全体神经元之间的联合适应性，减少过拟合的风险，增强泛化能力。

Dropout率的选择

经过交叉验证，隐含节点 Dropout 率等于 0.5 的时候效果最好，原因是 0.5 的时候 dropout 随机生成的网络结构最多。
Dropout 也可以被用作一种添加噪声的方法，直接对 input 进行操作。输入层设为更接近 1 的数。使得输入变化不会太大（0.8）
对参数 $w$ 的训练进行球形限制 (max-normalization)，对 dropout 的训练非常有用。
球形半径 $c$ 是一个需要调整的参数，可以使用验证集进行参数调优。
dropout 自己虽然也很牛，但是 dropout、max-normalization、large decaying learning rates and high momentum 组合起来效果更好，比如 max-norm regularization 就可以防止大的learning rate 导致的参数 blow up。
使用 pretraining 方法也可以帮助 dropout 训练参数，在使用 dropout 时，要将所有参数都乘以 $ 1/p $。

Dropout 缺点

增加训练时间：因为引入dropout之后相当于每次只是训练的原先网络的一个子网络，为了达到同样的精度需要的训练次数会增多。
代价函数 $J$ 不再被明确定义，每次迭代，都会随机移除一些节点，如果再三检查梯度下降的性能，实际上是很难进行复查的。定义明确的代价函数 $J$ 每次迭代后都会下降，因为我们所优化的代价函数 $J$ 实际上并没有明确定义，或者说在某种程度上很难计算，所以我们失去了调试工具来绘制这样的图片。我通常会关闭dropout函数，将keep-prob的值设为1，运行代码，确保 $J$ 函数单调递减。然后打开dropout函数，希望在dropout过程中，代码并未引入bug。我觉得你也可以尝试其它方法，虽然我们并没有关于这些方法性能的数据统计，但你可以把它们与dropout方法一起使用。

优化算法

梯度下降是目前神经网络中使用最为广泛的优化算法之一。为了弥补朴素梯度下降的种种缺陷，研究者们发明了一系列变种算法，优化算法经历了 SGD -> SGDM -> NAG -> AdaGrad -> AdaDelta -> RMSprop -> Adam -> NAdam 这样的发展历程。

Gradient Descent

梯度下降是指，在给定待优化的模型参数 $\theta \in \mathbb{R}^d$ 和目标函数 $J(\theta)$ 后，算法通过沿梯度 $\nabla_\theta J(\theta)$的相反方向更新 $\theta$ 来最小化 $J(\theta)$ 。学习率 $\eta$ 决定了每一时刻的更新步长。对于每个epoch $t$ ，我们可以用下述步骤描述梯度下降的流程：

(1) 计算目标函数关于参数的梯度
\[ g_t = \nabla_\theta J(\theta) \]
(2) 根据历史梯度计算一阶和二阶动量
\[ m_t = \phi(g_1, g_2, \cdots, g_t) \]

\[ v_t = \psi(g_1, g_2, \cdots, g_t) \]

(3) 计算当前时刻的下降梯度(步长) $\frac{m_t}{\sqrt{v_t + \epsilon}}$ ，并根据下降梯度更新模型参数
\[ \theta_{t+1} = \theta_t - \frac{m_t}{\sqrt{v_t + \epsilon}} \]
其中， $\epsilon$ 为平滑项，防止分母为零，通常取 $1e-8$ 。

注意：本文提到的步长，就是下降梯度。

Gradient Descent 和其算法变种

根据以上框架，我们来分析和比较梯度下降的各变种算法。

Vanilla SGD

朴素 SGD (Stochastic Gradient Descent) 最为简单，没有动量的概念，即
\[ m_t = \eta g_t \]

\[ v_t = I^2 \]

\[ \epsilon = 0 \]

这时，更新步骤就是最简单的
\[ \theta_{t+1}= \theta_t - \eta g_t \]
缺点：

收敛速度慢，而且可能会在沟壑的两边持续震荡
容易停留在一个局部最优点
如何合理的选择学习率也是 SGD 的一大难点

SGD with Momentum

为了抑制SGD的震荡，SGD-M认为梯度下降过程可以加入惯性(动量) Momentum[3]，加速 SGD 在正确方向的下降并抑制震荡。就好像下坡的时候，如果发现是陡坡，那就利用惯性跑的快一些。其在SGD的基础上，引入了一阶动量，然后进行更新：
\[ m_t = \gamma m_{t-1} + \eta g_t \\ \theta_{t+1}= \theta_t - m_t \]
即在原步长(SGD中是$\eta g_t$) 之上，增加了与上一时刻动量相关的一项 $\gamma m_{t-1}$，目的是结合上一时刻步长(下降梯度)，其中 $m_{t-1}$ 是上一时刻的动量，$\gamma$ 是动量因子。也就是说，$t$ 时刻的下降方向，不仅由当前点的梯度方向决定，而且由此前累积的下降方向决定，$\gamma$ 通常取 0.9 左右。这就意味着下降方向主要是此前累积的下降方向，并略微偏向当前时刻的下降方向。这使得参数中那些梯度方向变化不大的维度可以加速更新，并减少梯度方向变化较大的维度上的更新幅度。由此产生了加速收敛和减小震荡的效果。


图 1(a): SGD	图 1(b): SGD with momentum

从图 1 中可以看出，引入动量有效的加速了梯度下降收敛过程。

Nesterov Accelerated Gradient

SGD 还有一个问题是困在局部最优的沟壑里面震荡。想象一下你走到一个盆地，四周都是略高的小山，你觉得没有下坡的方向，那就只能待在这里了。可是如果你爬上高地，就会发现外面的世界还很广阔。因此，我们不能停留在当前位置去观察未来的方向，而要向前一步、多看一步、看远一些。

图 2: Nesterov update

NAG全称Nesterov Accelerated Gradient，则是在SGD、SGD-M的基础上的进一步改进，算法能够在目标函数有增高趋势之前，减缓更新速率。我们知道在时刻 $t$ 的主要下降方向是由累积动量决定的，自己的梯度方向说了也不算，那与其看当前梯度方向，不如先看看如果跟着累积动量走了一步后，那个时候再怎么走。因此，NAG在步骤1，不计算当前位置的梯度方向，而是计算如果按照累积动量走了一步，那个时候的下降方向：
\[ g_t = \nabla_\theta J(\theta - \gamma m_{t-1}) \tag{1} \]
参考图2理解：最初，SGD-M先计算当前时刻的梯度（短蓝向量）和累积动量（长蓝向量）进行参数更新。改进的方法NAG，先利用累积动量计算出下一时刻的 $\theta$ 的近似位置 $\theta - \gamma m_{t-1}$（棕向量），并根据该未来位置计算梯度（红向量）公式(1)，然后使用和 SGD-M 中相同的方式计算当前时刻的动量项(下降梯度)，进而得到完整的参数更新（绿向量），公式(2)即将该未来位置的梯度与累积动量计算当前时刻的动量项(下降梯度)：
\[ \begin{equation} \begin{split} m_t &= \gamma m_{t-1} + \eta g_t \\ &= \gamma m_{t-1} + \eta \nabla_\theta J(\theta - \gamma m_{t-1}) \end{split} \end{equation} \tag{2} \]

更新参数：
\[ \theta_{t+1} = \theta_t - m_t \tag{3} \]

这种计算梯度的方式可以使算法更好的「预测未来」，提前调整更新速率。

注意：
累积动量指的是上一时刻的动量乘上动量因子: $\gamma m_{t-1}$
当前时刻的动量项指的是: ${m_t}$
(上面的图只是为了助于理解，其中累积动量

Adagrad

SGD、SGD-M 和 NAG 均是以相同的学习率去更新 $\theta$ 的各个分量 $\theta_i$。而深度学习模型中往往涉及大量的参数，不同参数的更新频率往往有所区别。对于更新不频繁的参数（典型例子：更新 word embedding 中的低频词），我们希望单次步长更大，多学习一些知识；对于更新频繁的参数，我们则希望步长较小，使得学习到的参数更稳定，不至于被单个样本影响太多。

Adagrad在 $t$ 时刻对每一个参数 $\theta_i$ 使用了不同的学习率，我们首先介绍 Adagrad 对每一个参数的更新，然后我们对其向量化。为了简洁，令 $g_{t,i}$ 为在 $t$ 时刻目标函数关于参数 $θ_i$ 的梯度：
\[ g_{t, i} = \nabla_\theta J(\theta_{i}) \]
在 $t$ 时刻，对每个参数 $θ_i$ 的更新过程变为：
\[ \theta_{t+1, i} = \theta_{t, i} - \eta g_{t, i} \]
对于上述的更新规则，在 $t$ 时刻，我们要计算 $θ_i$ 从初始时刻到 $t$ 时刻的历史梯度平方和，来修正每一个参数 $θ_i$ 的学习率：
\[ \theta_{t+1, i}=\theta_{t, i}-\frac{\eta}{\sqrt{v_{t, i i}+\epsilon}} \cdot g_{t, i} \]
其中， $v_t \in \mathbb{R}^{d\times d}$ 是对角矩阵，其元素 $v_{t, ii}$ 为参数第 $i$ 维从初始时刻到 $t$ 时刻的梯度平方和。即通过引入二阶动量，来调整每一个参数的学习率，等效为 $\eta / \sqrt{v_t + \epsilon}$
\[ v_t = \text{diag}(\sum_{i=1}^t g_{i,1}^2, \sum_{i=1}^t g_{i,2}^2, \cdots, \sum_{i=1}^t g_{i,d}^2) \]
由于 $v_t$ 的对角线上包含了关于所有参数 $θ$ 的历史梯度的平方和，现在，我们可以通过 $v_t$ 和 $g_t$ 之间的元素向量乘法⊙向量化上述的操作：
\[ \theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{v_{t}+\epsilon}} \odot g_{t} \]
Adagrad算法的一个主要优点是无需手动调整学习率。在大多数的应用场景中，通常采用常数0.01。通过引入二阶动量，对于此前频繁更新过的参数，其二阶动量的对应分量较大，学习率就较小。这一方法在稀疏数据的场景下表现很好。但也存在一些问题：因为 $\sqrt{v_t}$ 是单调递增的，会使得学习率单调递减至0，可能会使得训练过程提前结束，即便后续还有数据也无法学到必要的知识。

AdaDelta

Adadelta 是 Adagrad 的一种扩展算法，以处理Adagrad学习速率单调递减的问题。考虑在计算二阶动量时，不是计算所有的历史梯度平方和，而只关注最近某一时间窗口内的下降梯度，Adadelta将计算历史梯度的窗口大小限制为一个固定值 $w$

在 Adadelta 中，无需存储先前的 $w$ 个平方梯度，而是将梯度的平方递归地表示成所有历史梯度平方的均值。在 $t$ 时刻的均值 $E[g^2]_t$ 只取决于先前的均值和当前的梯度（分量 $γ$ 类似于动量项）：
\[ E\left[g^{2}\right]_{t}=\gamma E\left[g^{2}\right]_{t-1}+(1-\gamma) g_{t}^{2} \]
我们将 $γ$ 设置成与动量项相似的值，即0.9左右。为了简单起见，我们利用参数更新向量 $Δθ_t$ 重新表示SGD的更新过程：

\[ \begin{array}{c}{\Delta \theta_{t}=-\eta \cdot g_{t, i}} \\ {\theta_{t+1}=\theta_{t}+\Delta \theta_{t}}\end{array} \]
我们先前得到的 Adagrad 参数更新向量变为：
\[ \Delta \theta_{t}=-\frac{\eta}{\sqrt{v_{t}+\epsilon}} \odot g_{t} \]
现在，我们简单将对角矩阵 $v_t$ 替换成历史梯度的均值 $E[g^2]_t$：
\[ \Delta \theta_{t}=-\frac{\eta}{\sqrt{E\left[g^{2}\right]_{t}+\epsilon}} g_{t} \]
由于分母仅仅是梯度的均方根（root mean squared，RMS）误差，我们可以简写为：
\[ \Delta \theta_{t}=-\frac{\eta}{R M S[g]_{t}} g_{t} \]
作者指出上述更新公式中的每个部分（与SGD，SDG-M 或者Adagrad）并不一致，即更新规则中必须与参数具有相同的假设单位。为了实现这个要求，作者首次定义了另一个指数衰减均值，这次不是梯度平方，而是参数的平方的更新：
\[ E\left[\Delta \theta^{2}\right]_{t}=\gamma E\left[\Delta \theta^{2}\right]_{t-1}+(1-\gamma) \Delta \theta_{t}^{2} \]
因此，参数更新的均方根误差为：
\[ R M S[\Delta \theta]_{t}=\sqrt{E\left[\Delta \theta^{2}\right]_{t}+\epsilon} \]
由于 $RMS[Δθ]_t$ 是未知的，我们利用参数的均方根误差来近似更新。利用 $RMS[Δθ]_{t−1}$ 替换先前的更新规则中的学习率 $η$，最终得到 Adadelta 的更新规则：
\[ \Delta \theta_{t}=-\frac{R M S[\Delta \theta]_{t-1}}{R M S[g]_{t}} g_{t} \]

\[ \theta_{t+1}=\theta_{t}+\Delta \theta_{t} \]

使用 Adadelta 算法，我们甚至都无需设置默认的学习率，因为更新规则中已经移除了学习率。

RMSprop

RMSprop 是一个未被发表的自适应学习率的算法，该算法由Geoff Hinton在其Coursera课堂的课程6e中提出。

RMSprop和Adadelta在相同的时间里被独立的提出，都起源于对Adagrad的极速递减的学习率问题的求解。实际上，RMSprop 是先前我们得到的 Adadelta 的第一个更新向量的特例：
\[ \begin{array}{l}{E\left[g^{2}\right]_{t}= γ E\left[g^{2}\right]_{t-1}+(1-γ) g_{t}^{2}} \\ {\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{E\left[g^{2}\right]_{t}+\epsilon}} g_{t}}\end{array} \]
同样，RMSprop 将学习率分解成一个平方梯度的指数衰减的平均。Hinton建议将 $γ$ 设置为0.9，对于学习率 $η$，一个好的固定值为0.001。

Adam

Adam 结合了Momentum 和 RMSprop 自适应梯度。Adam 中对一阶动量、二阶动量都使用指数衰减平均计算，即融合当前梯度和近一段时间内梯度的平均值，时间久远的梯度对当前平均值的贡献呈指数衰减。(β1， β2为衰减系数)
\[ m_t = \eta[ \beta_1 m_{t-1} + (1 - \beta_1)g_t ] \\ v_t = \beta_2 v_{t-1} + (1-\beta_2) \cdot \text{diag}(g_t^2) \]
其中，初值

\[ m_0 = 0 \\ v_0 = 0 \]
注意到，在迭代初始阶段，$m_t$ 和 $v_t$ 有一个向初值的偏移（过多的偏向了 0）。因此，可以对一阶和二阶动量做偏置校正 (bias correction)， (做偏移矫正的原理)
\[ \hat{m}_t = \frac{m_t}{1-\beta_1^t} \]

\[ \hat{v}_t = \frac{v_t}{1-\beta_2^t} \]
再进行更新，

\[ \theta_{t+1} = \theta_t - \frac{1}{\sqrt{\hat{v}_t} + \epsilon } \hat{m}_t \]
可以保证迭代较为平稳。

论文中建议参数为：$\beta_1 = 0.9，\beta_2 = 0.999， \epsilon = 10^{-8}$

深度学习为什么不用二阶优化

目前深度学习中，反向传播主要是依靠一阶梯度。二阶梯度在理论和实际上都是可以应用都网络中的，但相比于一阶梯度，二阶优化会存在以下一些主要问题：

计算量大，训练非常慢。
二阶方法能够更快地求得更高精度的解，这在浅层模型是有益的。而在神经网络这类深层模型中对参数的精度要求不高，甚至不高的精度对模型还有益处，能够提高模型的泛化能力。
稳定性。二阶方法能更快求高精度的解，同样对数据本身要的精度也会相应的变高，这就会导致稳定性上的问题。

预训练与微调(fine tuning)

什么是模型微调 fine tuning

用别人的参数、修改后的网络和自己的数据进行训练，使得参数适应自己的数据，这样一个过程，通常称之为微调（fine tuning).

微调时候网络参数是否更新

答案：会更新。finetune 的过程相当于继续训练，跟直接训练的区别是初始化的时候。

直接训练是按照网络定义指定的方式初始化。
finetune是用你已经有的参数文件来初始化。

fine-tuning 模型的三种状态

状态一：只预测，不训练
特点：相对快、简单，针对那些已经训练好，现在要实际对未知数据进行标注的项目，非常高效；
状态二：训练，但只训练最后分类层
特点：fine-tuning的模型最终的分类以及符合要求，现在只是在他们的基础上进行类别降维。
状态三：完全训练，分类层+之前卷积层都训练
特点：跟状态二的差异很小，当然状态三比较耗时和需要训练GPU资源，不过非常适合fine-tuning到自己想要的模型里面，预测精度相比状态二也提高不少。

ResNet

目的

解决网络“退化”问题，即当模型的层次加深时，错误率却提高的问题，如下图：

误差升高的原因是网络越深，梯度消失的现象就越明显，在反向传播的时候，无法有效的把梯度更新到前面的网络层，靠前的网络层参数无法更新，导致训练和测试效果变差。

针对这个问题，作者提出了一个Residual的结构来解决网络的退化问题。

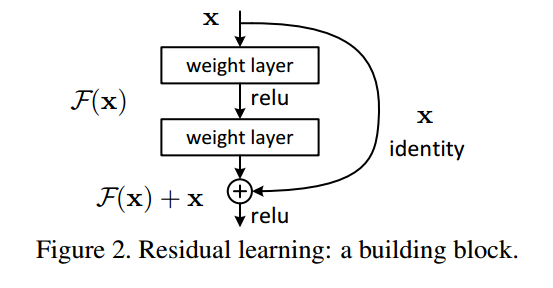
残差网络增加了一个identity mapping（恒等映射），把当前输出直接传输给下两层网络（全部是1:1传输，不增加额外的参数），相当于走了一个捷径，跳过了本层运算，这个直接连接命名为“skip connection”，同时在后向传播过程中，也是将下一层网络的梯度直接传递给上层网络，这样就解决了深层网络的梯度消失问题。此时需要学的函数 $H(x)$ 转换成 $F(x)+x$，即让 ResNet 学习的是残差函数 $F(x) = H(x) - x$。

输入 $x$ 经过两层的变换得到 $H(x)$ ，然后增加一个 $H(x)=x$ 的层，identity mapping（恒等映射），可以把当前输出直接传递给之后的层（没有增加额外的参数），相当于走了一个捷径，将原始所需要学的函数 $H(x)$ 转换成 $F(x)+x$，即让 ResNet 学习的是残差函数 $F(x) = H(x) - x$。

首先考虑两层神经网络的简单叠加（图a），输入 $x$ 经过两个网络层的变换得到 $H(x)$，激活函数采用ReLu，反向传播时，梯度将涉及两层参数的交叉相乘，可能会在离输入近的网络层中产生梯度消失的现象。ResNet残差网络增加了一个 identity mapping(恒等映射)，既然离输入近的神经网络层较难训练，那么我们可以将它短接到更靠近输出的层（图b），输入 $x$ 经过两个神经网络的变换得到 $H(x)$，同时也短接到两层之后，最后这个包含两层的神经网络模块输出$H(x)=F(x)+x$。这样一来， $F(x)$ 被设计为只需要拟合输入 $x$ 与目标输出 $H(x)$ 的残差 $H(x)-x$ ，残差网络的名称也因此而来。如果某一层的输出已经较好的拟合了期望结果，那么多加入一层不会使得模型变得更差，因为该层的输出将直接被短接到两层之后，相当于直接学习了一个恒等映射，而跳过的两层只需要拟合上层输出和目标之间的残差即可。

即增加一个 $H(x)=x$ 的层，identity mapping（恒等映射），将原始所需要学的函数 $H(x)$ 转换成 $F(x)+x$，即让 ResNet 学习的是残差函数 $F(x) = H(x) - x$。这里如果 $F(x) = 0$, 那么就是上面提到的恒等映射。事实上，ResNet是“shortcut connections”的在connections是在恒等映射下的特殊情况，它没有引入额外的参数和计算复杂度。假如优化目标函数是逼近一个恒等映射，而不是0映射，那么学习找到对恒等映射的扰动会比重新学习一个映射函数要容易。从下图可以看出，残差函数一般会有较小的响应波动，表明恒等映射是一个合理的预处理。

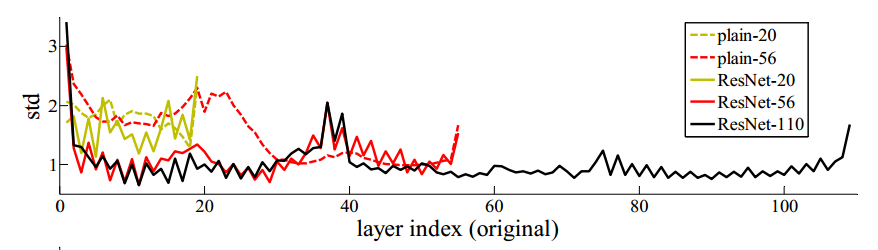
分析残差块结构：

它有二层，如下表达式，其中 $σ$ 代表非线性函数 ReLU
\[ \mathcal{F}=W_{2} \sigma\left(W_{1} \mathbf{x}\right) \]
然后通过一个shortcut，和第2个ReLU，获得输出 $y$
\[ \mathbf{y}=\mathcal{F}\left(\mathbf{x},\left\{W_{i}\right\}\right)+\mathbf{x} \]
当需要对输入和输出维数进行变化时（如改变通道数目），可以在shortcut时对 $x$ 做一个线性变换$W_s$，如下式，然而实验证明 $x$ 已经足够了，不需要再搞个维度变换，除非需求是某个特定维度的输出，如文章开头的 ResNet 网络结构图中的虚线，是将通道数翻倍。
\[ \mathbf{y}=\mathcal{F}\left(\mathbf{x},\left\{W_{i}\right\}\right)+W_{s} \mathbf{x} \]
实验证明，这个残差块往往需要两层以上，单单一层的残差块 $(y=W_1x+x)$ 并不能起到提升作用。
残差网络的确解决了退化的问题，在训练集和校验集上，都证明了的更深的网络错误率越小，如下图

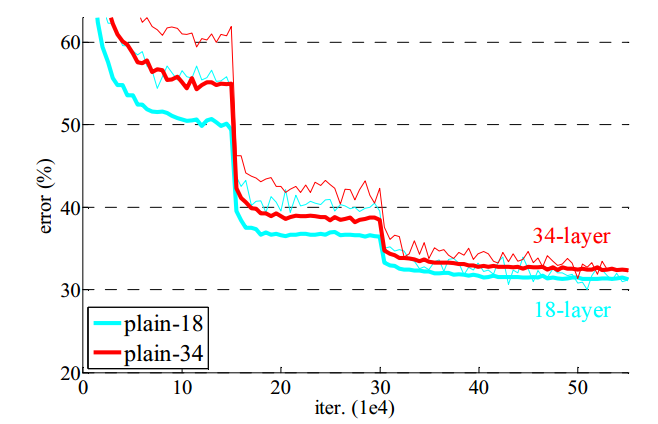
实际中，考虑计算的成本，对残差块做了计算优化，即将两个 3x3的卷积层替换为1x1 + 3x3 + 1x1, 如下图。新结构中的中间 3x3 的卷积层首先在一个降维1x1卷积层下减少了计算，然后在另一个1x1的卷积层下做了还原，既保持了精度又减少了计算量。

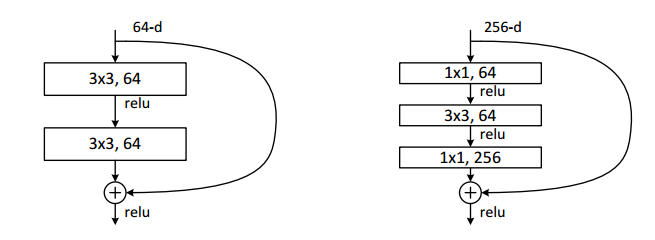
Reference

Caffe

Caffe卷积层的实现

Caffe的卷积层实现，使用 im2col 操作，将数据以及卷积核分别转换成新的矩阵，然后将两对矩阵进行内积运算（inner product)。这样做，比原始的卷积操作速度更快。

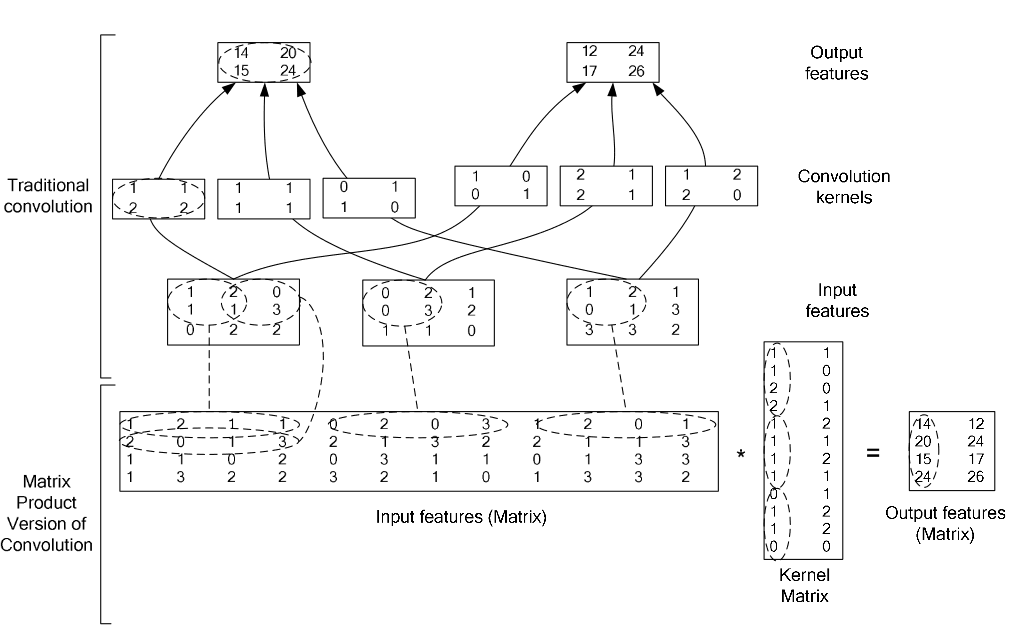
其中 im2col : 将一个大矩阵，重叠地划分为多个子矩阵，对每个子矩阵序列化成向量，最后得到另外一个矩阵。

Caffe 结构

Caffe’s Abstract Framework:

Blob：是Caffe中 数据传输的媒介，相当于一个 N 维数组。网络中的输入数据、权重参数等，都是转化为Blob数据结构来存储。而实际上，它们只是一维的指针而已，其4维结构通过shape属性得以计算出来。

Blob中重要的函数和成员有：

data_：数据

// 获取 cpu 数据的方法
const Dtype* bottom_data = bottom[0]->cpu_data(); // 获得输入的blob指针 （只读，不能改变数据内容）
Dtype* top_data = top[0]->mutable_cpu_data();	// 获得输出blob的data指针 （读写，可以改变数据内容）

// 获取 gpu 数据的方法
const Dtype* bottom_data = bottom[0]->gpu_data();	// 只读
Dtype* top_data = top[0]->mutable_gpu_data();		// 读写

diff_ ：梯度

1 2	const Dtype* top_diff = top[0]->cpu_diff(); // 只读 Dtype* bottom_diff = bottom[0]->mutable_cpu_diff(); // 读写

Reshape() ：重新修改Blob的形状(4维)，并根据形状来申请动态内存存储数据和梯度。
count()：计算Blob所需要的基本数据单元的数量。
Layer：作为网络的基础单元，层与层之间的数据节点、前向传递，后向传递都在该数据结构中被实现。层的种类有：卷积层、池化层、激活层、全连接层，Data层等，还可以自己添加所需要的层。

从bottom进行数据的输入 ，计算后，通过top进行输出。图中的黄色多边形表示输入输出的数据，蓝色矩形表示层。
每一种类型的层都定义了三种关键的计算：setup,forward and backword
（1）setup: 层的建立和初始化，以及在整个模型中的连接初始化。
（2）forward: 从bottom得到输入数据，进行计算，并将计算结果送到top，进行输出。
（3）backward: 从层的输出端top得到数据的梯度，计算当前层的梯度，并将计算结果送到bottom,向前传递。

Net：则是由多个layer组合而成。作为网络的整体骨架，决定了网络中的层次数目以及各个层的类别等信息。
Solver：作为网络的求解策略，主要包括使用何种方法进行优化，比如随机梯度下降还是，自适应梯度下降等，以及学习率等一些配置等。

=============================================================================

添加新的一层

1）在./src/caffe/proto/caffe.proto 中增加对应 layer 的 paramter message；

2）在 ./include/caffe/***layers.hpp中增加该 layer 的类的声明，***表示有common_layers.hpp ， data_layers.hpp， neuron_layers.hpp， vision_layers.hpp 和 loss_layers.hpp 等；

3）在 ./src/caffe/layers/ 目录下新建 .cpp和.cu文件，进行类实现。

4）在 ./src/caffe/gtest/ 中增加 layer 的测试代码，对所写的 layer 前传和反传进行测试，测试还包括速度。

relu_layer.cpp

#include <algorithm>
#include <vector>
#include "caffe/layers/relu_layer.hpp"
namespace caffe {

// 前向传递
template <typename Dtype>
void ReLULayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
    const vector<Blob<Dtype>*>& top) {
  // (只读)获得输入blob的data指针
  const Dtype* bottom_data = bottom[0]->cpu_data();	
  // （读写）获得输出 blob 的 data 指针
  Dtype* top_data = top[0]->mutable_cpu_data(); 
  // 获得输入 blob 元素个数
  const int count = bottom[0]->count();
  // Leaky ReLU参数，从layer_param_ 中获得，默认为0，即普通ReLU
  Dtype negative_slope = this->layer_param_.relu_param().negative_slope();
  for (int i = 0; i < count; ++i) {
    // 执行 ReLU 操作
    top_data[i] = std::max(bottom_data[i], Dtype(0))
        + negative_slope * std::min(bottom_data[i], Dtype(0));
  }
}

// 反向传播
template <typename Dtype>
void ReLULayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top,
    const vector<bool>& propagate_down,
    const vector<Blob<Dtype>*>& bottom) {
  // 如果需要做反向传播计算
  if (propagate_down[0]) {
    // （只读）获得前一层的data指针
    const Dtype* bottom_data = bottom[0]->cpu_data();
    // （只读）获得后一层的diff指针
    const Dtype* top_diff = top[0]->cpu_diff();
    // （读写）获得前一层的diff指针
    Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
    // 获得需要参与计算的元素总数
    const int count = bottom[0]->count();
    // Leaky ReLU参数，姑且认为是0
    Dtype negative_slope = this->layer_param_.relu_param().negative_slope();
    for (int i = 0; i < count; ++i) {
      // ReLU的导函数就是 （bottom_data[i] > 0），根据求导链式法则，后一层的误差乘以导函数的误差
      bottom_diff[i] = top_diff[i] * ((bottom_data[i] > 0)
          + negative_slope * (bottom_data[i] <= 0));
    }
  }
}

#ifdef CPU_ONLY
STUB_GPU(ReLULayer);
#endif

INSTANTIATE_CLASS(ReLULayer);
}  // namespace caffe

《深度学习21天实战Caffe》P94 中有讲一点源码

=============================================================================

1. Blob：

1.1. Blob的类型描述

Caffe内部采用的数据类型主要是对protocol buffer所定义的数据结构的继承，因此可以在尽可能小的内存占用下获得很高的效率，虽然追求性能的同时Caffe也会牺牲了一些代码可读性。
直观来说，可以把Blob看成一个有4维的结构体（包含数据和梯度），而实际上，它们只是一维的指针而已，其4维结构通过shape属性得以计算出来。

1.2. Blob的重要成员函数和变量

1 2	shared_ptr<SyncedMemory> data_ //数据 shared_ptr<SyncedMemory> diff_ //梯度

重新修改Blob的形状(4维)，并根据形状来申请动态内存存储数据和梯度。

1 2	void Blob<Dtype>::Reshape(const int num, const int channels, const int height, const int width)

计算Blob所需要的基本数据单元的数量。

1	inline int count(int start_axis, int end_axis) const

2. Layer：

2.1. Layer的类型描述

Layer是网络模型和计算的核心，在数据存储上，主要分成bottom_vecs、top_vecs、weights&bias三个部分；在数据传递上，也主要分为LayerSetUp、Reshape、Forward、Backward四个过程，符合直观上对层与层之间连接的理解，贴切自然。

2.2. Layer的重要成员函数和变量

通过bottom Blob对象的形状以及LayerParameter(从prototxt读入)来确定Layer的学习参数（以Blob类型存储）的形状。

1 2	vector<Dtype> loss_ //每一层都会有一个loss值，但只有LossLayer才会产生非0的loss vector<shared_ptr<Blob<Dtype> > > blobs_ //Layer所学习的参数，包括权值和偏差

1 2	virtual void LayerSetUp(const vector<Blob<Dtype>>& bottom, const vector<Blob<Dtype>>& top)

通过bottom Blob对象的形状以及Layer的学习参数的形状来确定top Blob对象的形状。

1 2	virtual void Reshape(const vector<Blob<Dtype>>& bottom, const vector<Blob<Dtype>>& top)

Layer内部数据正向传播，从bottom到top方向。

1 2	virtual void Forward(const vector<Blob<Dtype>> &bottom, vector<Blob<Dtype>> *top) = 0

Layer内部梯度反向传播，从top到bottom方向。

1
2
3

virtual void Backward(const vector<Blob<Dtype>*> &top,
                      const vector<bool> &propagate_down, 
                      vector<Blob<Dtype>*> *bottom) = 0

3. Net：

3.1. Net的类型描述

Net用容器的形式将多个Layer有序地放在一起，其自身实现的功能主要是对逐层Layer进行初始化，以及提供Update( )的接口（更新网络参数），本身不能对参数进行有效地学习过程。

3.2. Net的重要成员函数和变量

根据NetParameter进行net初始化,简单的来说就是先把网络中所有层的bottom Blobs&top Blobs（无重复）实例化，并从输入层开始，逐层地进行Setup的工作，从而完成了整个网络的搭建，为后面的数据前后传输打下基础。

vector<shared_ptr<Layer<Dtype> > > layers_ //构成该net的layers
vector<vector<Blob<Dtype>*> > bottom_vecs_ //每一层layer中的bottom Blobs
vector<vector<Blob<Dtype>*> > top_vecs_ //每一层layer中的top Blobs
vector<shared_ptr<Blob<Dtype> > > params_ //整个net中的learnable parameter

1	void Init(const NetParameter& param)

是对整个网络的前向和方向传导，各调用一次就可以计算出网络的loss了。

1
2
3

vector<Blob<Dtype>*>& Forward(const vector<Blob<Dtype>* > & bottom,
                              Dtype* loss = NULL)
void Net<Dtype>::Backward()

4. Solver

4.1. Solver的类型描述

Solver类中包含一个Net的指针，主要是实现了训练模型参数所采用的优化算法，根据优化算法的不同会派生不同的类，而基于这些子类就可以对网络进行正常的训练过程。

4.2. Solver的重要成员函数和变量

对已初始化后的网络进行固定次数的训练迭代过程。

1	shared_ptr<Net<Dtype> > net_ //net对象

1	void Step(int iters)

对已初始化后的网络进行固定次数的训练迭代过程。

1 2	ComputeUpdateValue(); net_->Update();

CUDA编程 *

1. 概念

CUDA编程可以利用GPUs的并行计算引擎来更加高效地解决比较复杂的计算难题。在CUDA中，有两个比较重要的概念，host 和 device。

host：指代CPU及其内存
device：指代GPU及其内存

CUDA程序中既包含host程序，又包含device程序，它们分别在CPU和GPU上运行。同时，host与device之间可以进行通信，这样它们之间可以进行数据拷贝。典型的CUDA程序的执行流程如下：

分配host内存，并进行数据初始化；
分配device内存，并从host将数据拷贝到device上；
调用CUDA的核函数在device上完成指定的运算；
将device上的运算结果拷贝到host上；
释放device和host上分配的内存。

上面流程中最重要的一个过程是调用CUDA的核函数来执行并行计算，kernel 是在device上线程中并行执行的函数，核函数用__global__符号声明，在调用时需要用<<<grid, block>>>来指定kernel要执行的线程数量，在CUDA中，每一个线程都要执行核函数，并且每个线程会分配一个唯一的线程号thread ID，这个ID值可以通过核函数的内置变量threadIdx来获得。

GPU上很多并行化的轻量级线程。kernel在device上执行时实际上是启动很多线程，一个kernel所启动的所有线程称为一个网格（grid），同一个网格上的线程共享相同的全局内存空间，grid是线程结构的第一层次，而网格又可以分为很多线程块（block），一个线程块里面包含很多线程，这是第二个层次。线程两层组织结构如下图所示，这是一个gird和block均为2-dim的线程组织。grid和block都是定义为dim3类型的变量，dim3可以看成是包含三个无符号整数（x，y，z）成员的结构体变量，在定义时，缺省值初始化为1。因此grid和block可以灵活地定义为1-dim，2-dim以及3-dim结构，对于图中结构（主要水平方向为x轴），定义的grid和block如下所示，kernel在调用时也必须通过执行配置<<<grid, block>>>来指定kernel所使用的线程数及结构。

1
2
3

dim3 grid(3, 2);
dim3 block(5, 3);
kernel_fun<<< grid, block >>>(prams...);

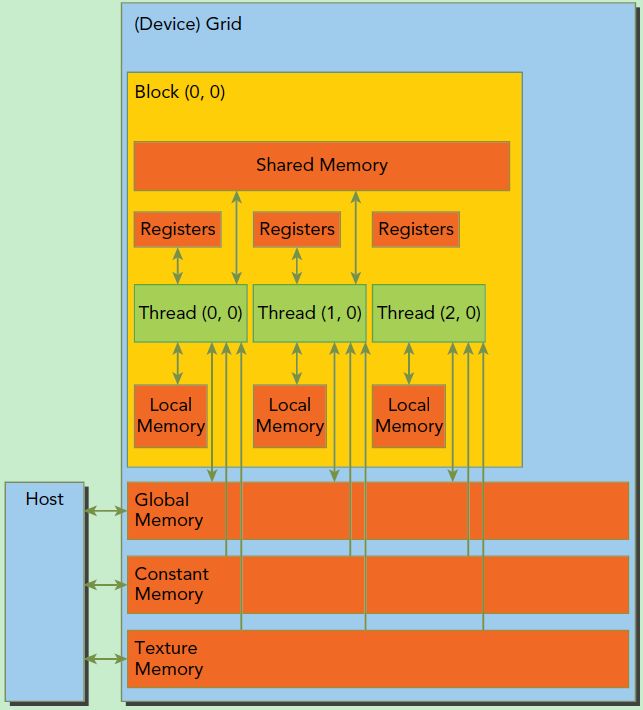
2. 实战

（1）向量加法

实现一个向量加法的实例，这里grid和block都设计为1-dim，首先定义kernel如下：

// 两个向量加法kernel，grid和block均为一维
__global__ void add(float* x, float * y, float* z, int n)
{
    // 获取全局索引
    int index = threadIdx.x + blockIdx.x * blockDim.x;
    // 步长
    int stride = blockDim.x * gridDim.x;
    for (int i = index; i < n; i += stride)
    {
        z[i] = x[i] + y[i];
    }
}

其中stride是整个grid的线程数，有时候向量的元素数很多，这时候可以将在每个线程实现多个元素（元素总数/线程总数）的加法，相当于使用了多个grid来处理，这是一种grid-stride loop方式，不过下面的例子一个线程只处理一个元素，所以kernel里面的循环是不执行的。下面我们具体实现向量加法：

int main()
{
    int N = 1 << 20;
    int nBytes = N * sizeof(float);
    // 申请host内存
    float *x, *y, *z;
    x = (float*)malloc(nBytes);
    y = (float*)malloc(nBytes);
    z = (float*)malloc(nBytes);

    // 初始化数据
    for (int i = 0; i < N; ++i)
    {
        x[i] = 10.0;
        y[i] = 20.0;
    }

    // 申请device内存
    float *d_x, *d_y, *d_z;
    cudaMalloc((void**)&d_x, nBytes);
    cudaMalloc((void**)&d_y, nBytes);
    cudaMalloc((void**)&d_z, nBytes);

    // 将host数据拷贝到device
    cudaMemcpy((void*)d_x, (void*)x, nBytes, cudaMemcpyHostToDevice);
    cudaMemcpy((void*)d_y, (void*)y, nBytes, cudaMemcpyHostToDevice);
    // 定义kernel的执行配置
    dim3 blockSize(256);
    dim3 gridSize((N + blockSize.x - 1) / blockSize.x);
    // 执行kernel
    add << < gridSize, blockSize >> >(d_x, d_y, d_z, N);

    // 将device得到的结果拷贝到host
    cudaMemcpy((void*)z, (void*)d_z, nBytes, cudaMemcpyHostToDevice);

    // 检查执行结果
    float maxError = 0.0;
    for (int i = 0; i < N; i++)
        maxError = fmax(maxError, fabs(z[i] - 30.0));
    std::cout << "最大误差: " << maxError << std::endl;

    // 释放device内存
    cudaFree(d_x);
    cudaFree(d_y);
    cudaFree(d_z);
    // 释放host内存
    free(x);
    free(y);
    free(z);

    return 0;
}

这里我们的向量大小为1<<20，而block大小为256，那么grid大小是4096，kernel的线程层级结构如下图所示：

（2）矩阵乘法

最后我们再实现一个稍微复杂一些的例子，就是两个矩阵的乘法，设输入矩阵为 A 和 B ，要得到 C = A x B 。实现思路是每个线程计算 C 的一个元素值 $C_{i, j}$ ，对于矩阵运算，应该选用 grid 和block为2-D的。首先定义矩阵的结构体：

// 矩阵类型，行优先，M(row, col) = *(M.elements + row * M.width + col)
struct Matrix
{
    int width;
    int height;
    float *elements;
};

然后实现矩阵乘法的核函数，这里我们定义了两个辅助的__device__函数分别用于获取矩阵的元素值和为矩阵元素赋值，具体代码如下：

// 获取矩阵A的(row, col)元素
__device__ float getElement(Matrix *A, int row, int col)
{
	return A->elements[row * A->width + col];
}

// 为矩阵A的(row, col)元素赋值
__device__ void setElement(Matrix *A, int row, int col, float value)
{
	A->elements[row * A->width + col] = value;
}

// 矩阵相乘kernel，2-D，每个线程计算一个元素
__global__ void matMulKernel(Matrix *A, Matrix *B, Matrix *C)
{
	float Cvalue = 0.0;
	int row = threadIdx.y + blockIdx.y * blockDim.y;
	int col = threadIdx.x + blockIdx.x * blockDim.x;
	for (int i = 0; i < A->width; ++i)
	{
		Cvalue += getElement(A, row, i) * getElement(B, i, col);
	}
	setElement(C, row, col, Cvalue);
}

最后我们采用统一内存编写矩阵相乘的测试实例：

int main()
{
    int width = 1 << 10;
    int height = 1 << 10;
    Matrix *A, *B, *C;
    // 申请托管内存
    cudaMallocManaged((void**)&A, sizeof(Matrix));
    cudaMallocManaged((void**)&B, sizeof(Matrix));
    cudaMallocManaged((void**)&C, sizeof(Matrix));
    int nBytes = width * height * sizeof(float);
    cudaMallocManaged((void**)&A->elements, nBytes);
    cudaMallocManaged((void**)&B->elements, nBytes);
    cudaMallocManaged((void**)&C->elements, nBytes);

    // 初始化数据
    A->height = height;
    A->width = width;
    B->height = height;
    B->width = width;
    C->height = height;
    C->width = width;
    for (int i = 0; i < width * height; ++i)
    {
        A->elements[i] = 1.0;
        B->elements[i] = 2.0;
    }

    // 定义kernel的执行配置
    dim3 blockSize(32, 32);
    dim3 gridSize((width + blockSize.x - 1) / blockSize.x, 
        (height + blockSize.y - 1) / blockSize.y);
    // 执行kernel
    matMulKernel << < gridSize, blockSize >> >(A, B, C);


    // 同步device 保证结果能正确访问
    cudaDeviceSynchronize();
    // 检查执行结果
    float maxError = 0.0;
    for (int i = 0; i < width * height; ++i)
        maxError = fmax(maxError, fabs(C->elements[i] - 2 * width));
    std::cout << "最大误差: " << maxError << std::endl;

    return 0;
}

*常考问题

全连接层作用

(1) 全连接层：在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。

(2) 全连接是个矩阵乘法，相当于一个特征空间变换，可以把有用的信息提取整合。再加上激活函数的非线性映射，多层全连接层理论上可以模拟任何非线性变换。

(3) 全连接还有一个作用是维度变换，尤其是可以把高维变到低维，同时把有用的信息保留下来。

但全连接层的缺点也很明显：

参数数量太大
无法保持空间结构（没有利用像素之间的位置信息）
网络层数限制

N个节点的全连接可近似为N个模板卷积后的均值池化(GAP)
不同channel同一位置上的全连接等价与1x1的卷积

1
2
3

以VGG-16为例，对224x224x3的输入，最后一层卷积可得输出为7x7x512，如后层是一层含4096个神经元的FC，则可用卷积核为7x7x512x4096的全局卷积来实现这一全连接运算过程，其中该卷积核参数如下：“filter size = 7, padding = 0, stride = 1, D_in = 512, D_out = 4096”经过此卷积操作后可得输出为1x1x4096

如需再次叠加一个2048的FC，则可设定参数为“filter size = 1, padding = 0, stride = 1, D_in = 4096, D_out = 2048”的卷积层操作。

卷积的意义与作用

卷积层：可以看做是全连接的一种简化形式：通过局部连接 + 权值共享，大大减少了参数并且使得训练变得可控，同时还保留了空间位置信息。通过使用多个filter来提取图片的不同特征，再加上Pooling 层下采样，进一步减少参数数量，同时还可以提升模型的鲁棒性。

数学、物理角度理解卷积

卷积层参数、计算量(FLOPs)

深度学习框架FLOPs： Floating point operations，浮点运算数量。

输入特征尺寸为：$H_1 \times W_1 \times C_{in}$

卷积核尺寸为：$K \times K \times C_{in} \times C_{out}$

输出特征尺寸为：$H_2 \times W_2 \times C_{out}$

Feature map 计算公式：$H_2 = \frac{H_1 - K + 2P}{S} + 1$

卷积层参数计算 Parameters
$(K \times K \times C_{in}) \times C_{out}$ (不考虑 $bias$)
$(K \times K \times C_{in} + 1) \times C_{out}$ (考虑 $bias$)
卷积计算量 FLOPs
$(K \times K \times C_{in}) \times C_{out} \times W_2 \times H_2$ (不考虑 $bias$)

Reference: 卷积神经网络的复杂度分析

2D卷积

平时用的卷积就是2D卷积，即滤波器深度与输入层深度一样。

2D卷积

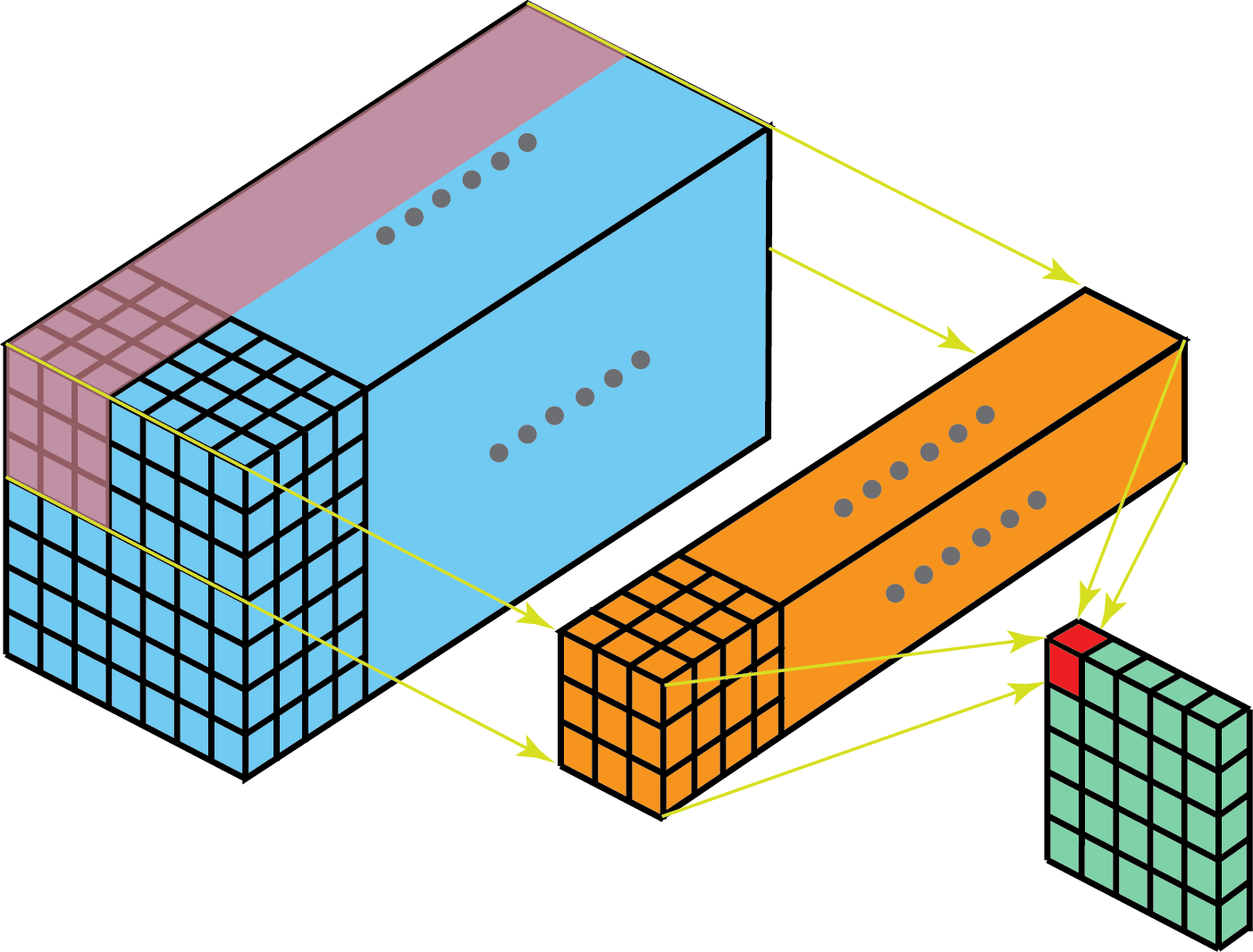
3D 卷积

滤波器的深度小于输入层深度（核大小<通道大小）。因此，3D 过滤器可以在所有三个方向（图像的高度、宽度、通道）上移动。在每个位置，逐元素的乘法和加法都会提供一个数值。因为过滤器是滑过一个 3D 空间，所以输出数值也按 3D 空间排布。也就是说输出是一个 3D 数据。3D 卷积可以描述 3D 空间中目标的空间关系。对某些应用（比如生物医学影像中的 3D 分割/重构）而言，这样的 3D 关系很重要，比如在 CT 和 MRI 中，血管之类的目标会在 3D 空间中蜿蜒曲折。

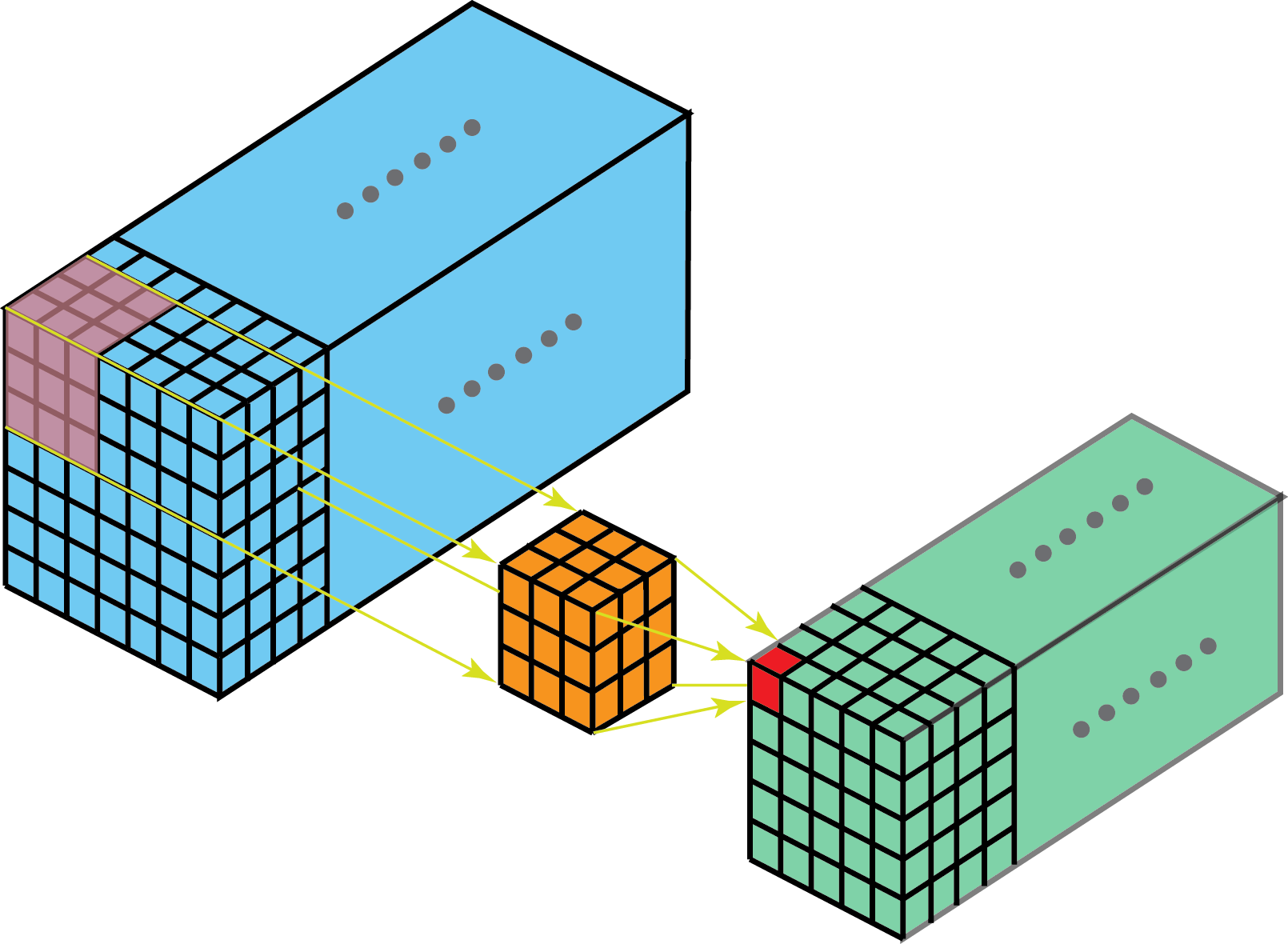
3D卷积

1 x 1 卷积

进行升维和降维的作用，也就是通过控制卷积核（通道数）实现。这个可以帮助减少模型参数，也可以对不同特征进行尺寸的归一化；同时也可以用于不同channel上特征的融合。如，RPN网络中，网络输出，接入了两个并行的1x1的卷积层，来回归anchor的所属类别以及需要做的平移缩放参数。conv5_3 输出[38x50x512]，输入到cls_layer 得到 [38x50x18]，以及 loc_layer 得到 [38x50x4].

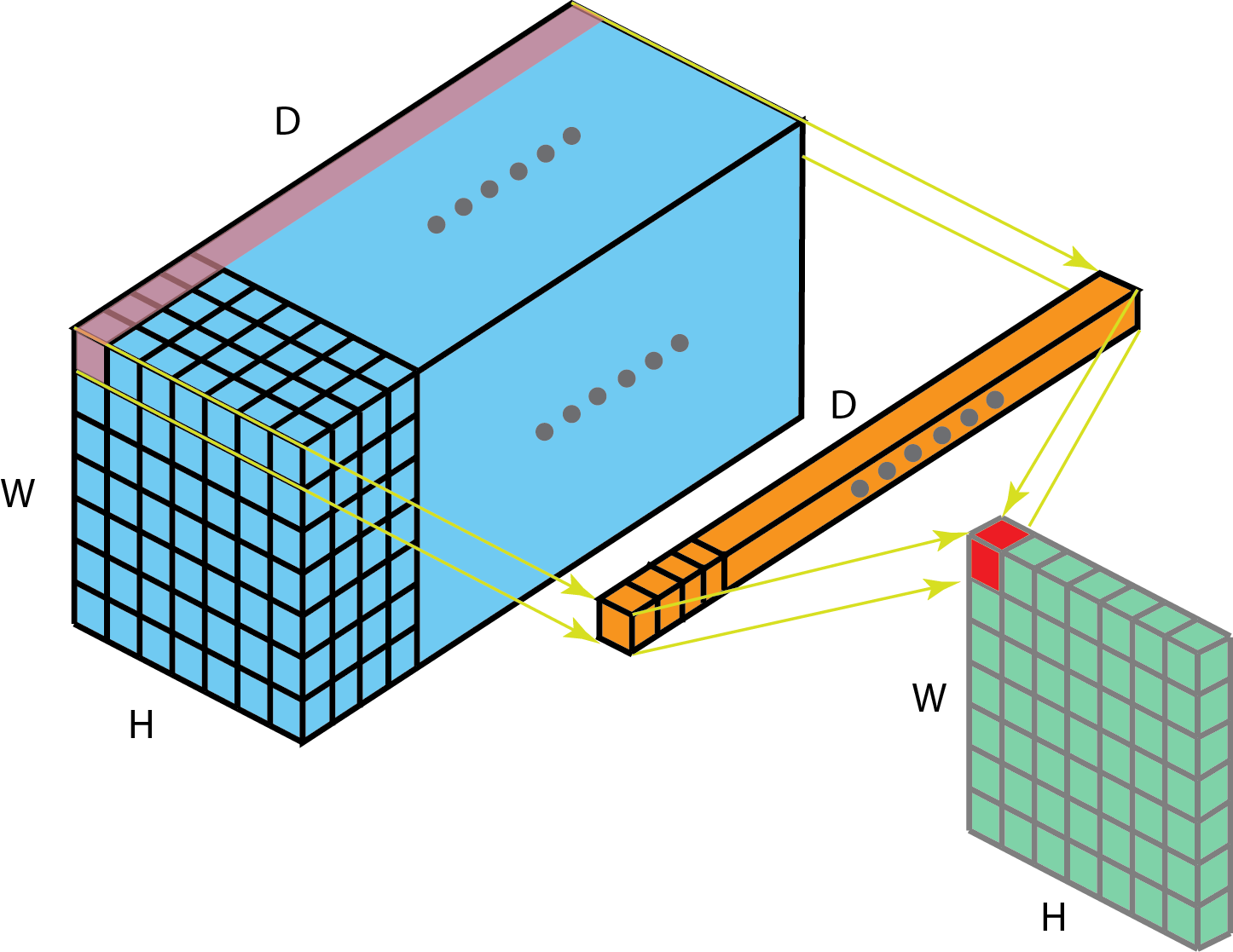
1*1卷积

转置卷积（反卷积、去卷积）

反卷积：是一种特殊的正向卷积，先按照一定的比例通过补 0 来扩大输入图像的尺寸，接着将卷积核进行转置，再进行正向卷积。
作用：实现图像由小分辨率到到大分辨率的映射操作，其在在 FCN 语义分割网络中有应用。1 2 3

上采样：由于输入图像通过卷积神经网络(CNN)提取特征后，输出的尺寸往往会变小，而有时我们需要将图像恢复到原来的尺寸以便进行进一步的计算(e.g.:图像的语义分割)，这个采用扩大图像尺寸，实现图像由小分辨率到大分辨率的映射的操作，叫做上采样(Upsample)
上采样有3种常见的方法：

双线性插值(bilinear)

反卷积(Transposed Convolution)

反池化(Unpooling)

1. 解释：

在卷积中，我们定义 C 为卷积核，Large 为输入图像，Small 为输出图像。经过卷积（矩阵乘法）后，我们将大图像下采样为小图像。这种矩阵乘法的卷积的实现遵照：C x Large = Small。

下面的例子展示了这种运算的工作方式。它将输入平展为 16×1 的矩阵，并将卷积核转换为一个稀疏矩阵（4×16）。然后，在稀疏矩阵和平展的输入之间使用矩阵乘法。之后，再将所得到的矩阵（4×1）转换为 2×2 的输出。

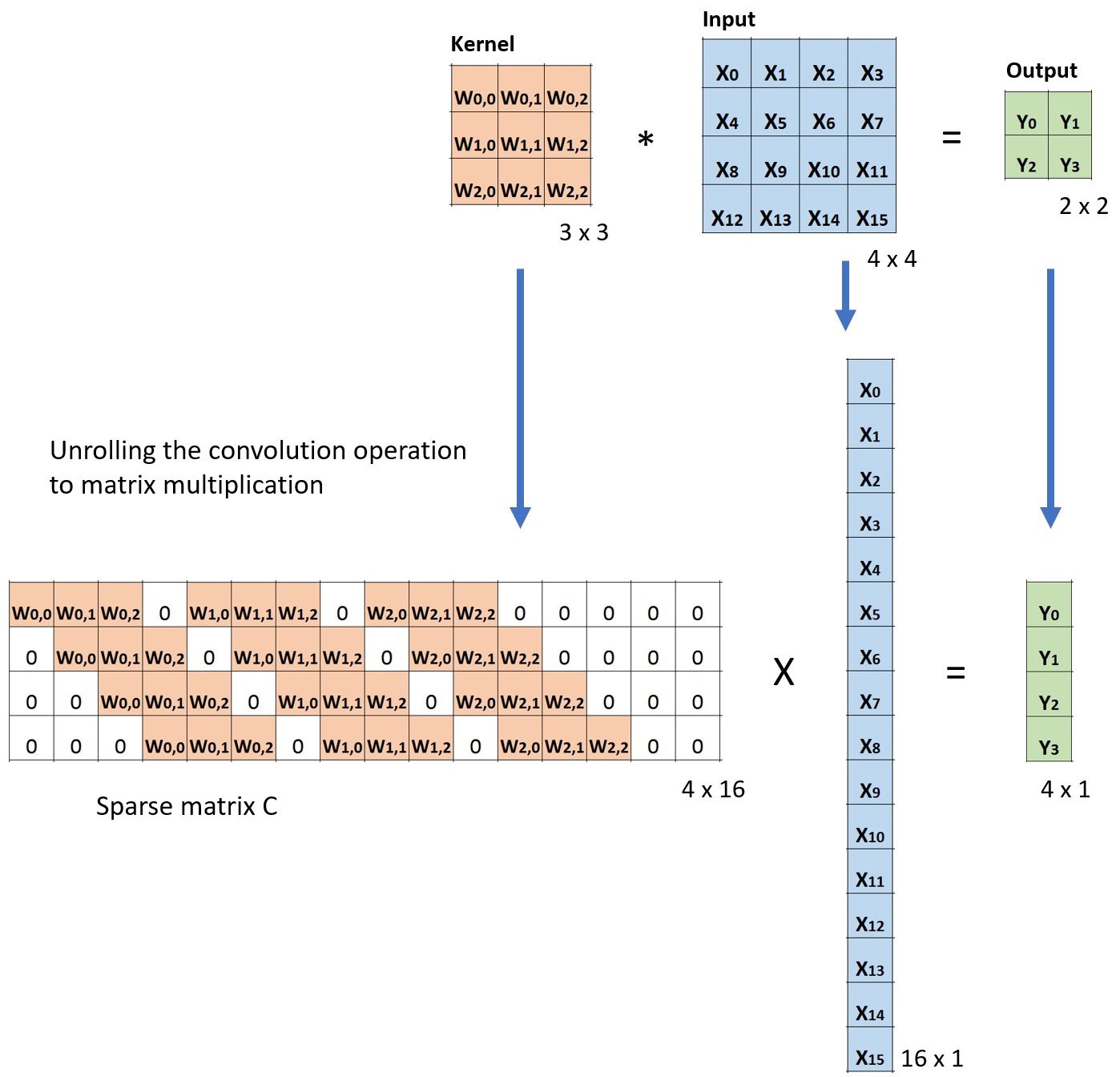
卷积的矩阵乘法：将 Large 输入图像（4×4）转换为 Small 输出图像（2×2）

现在，如果我们在等式的两边都乘上矩阵的转置 $C^T$，并借助「一个矩阵与其转置矩阵的乘法得到一个单位矩阵」这一性质，那么我们就能得到公式 $C^T$ x Small = Large，如下图所示。

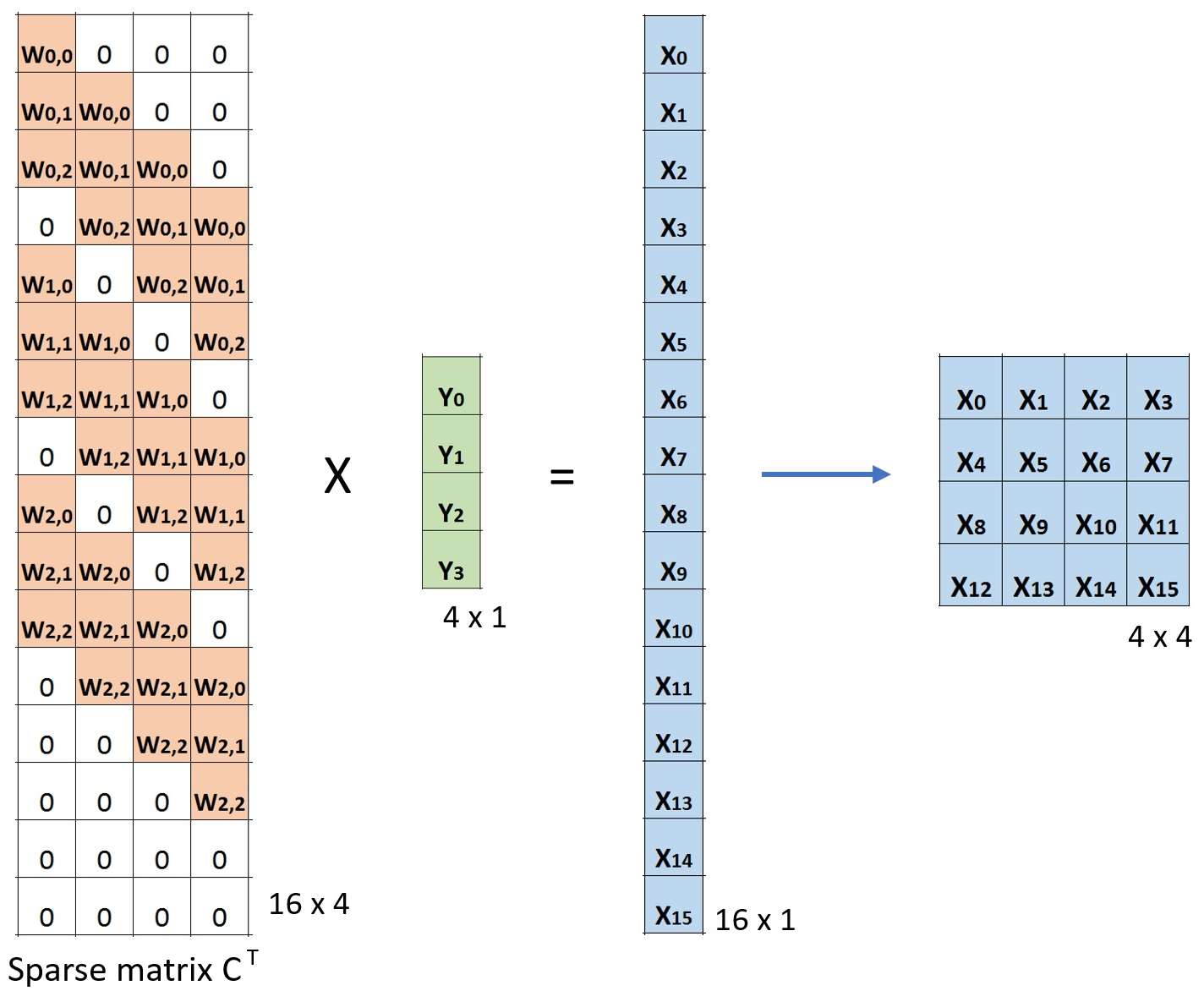
卷积的矩阵乘法：将 Small 输入图像（2×2）转换为 Large 输出图像（4×4）

正向卷积的计算公式为：

步长 $strides = 1$，填充 $padding = 0$ ，即 $i=4, k=3, s=1, p=0$ ，

则按照卷积计算公式 $o=\frac{i+2 p-k}{s}+1$ ，输出图像 $output$ 的尺寸为 $2 * 2$。

反卷积的输入输出尺寸关系：

若：$(o+2 p-k) \% s=0$

此时反卷积的输入尺寸为：

$o=s(i-1)-2 p+k$

若：$(o+2 p-k) \% s \neq 0$

此时反卷积的输入输出尺寸关系为：

$o=s(i-1)-2 p+k+(o+2 p-k) \% s$

（具体的图像待补充！）

2. 举例：通过应用各种填充和步长，我们可以将同样的 2×2 输入图像映射到不同的图像尺寸。

（1）将 2 x 2 的输入上采样成 4 x 4的输出

在一个 2×2 的输入（周围加了 2×2 的单位步长的零填充）上应用一个 3×3 核的转置卷积。上采样输出的大小是 4×4。

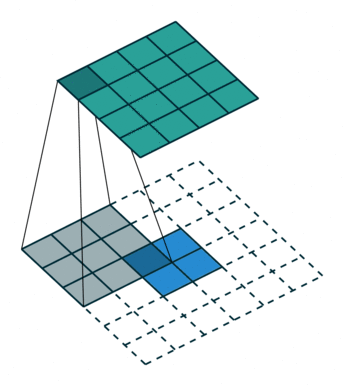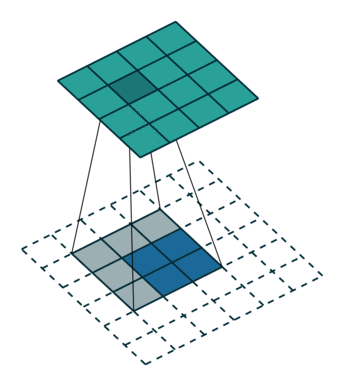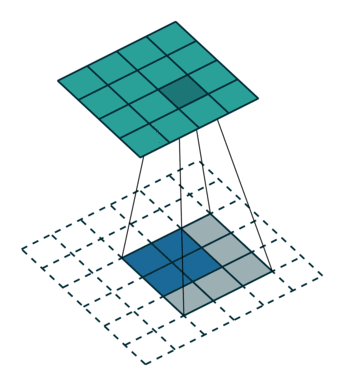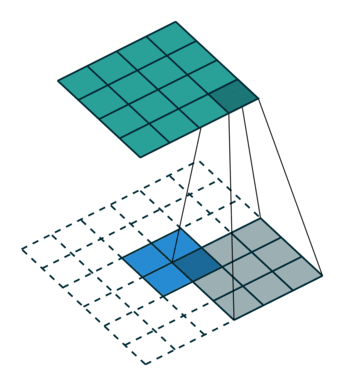
转置卷积(反卷积)

（2）将 2×2 的输入上采样成 5×5 的输出

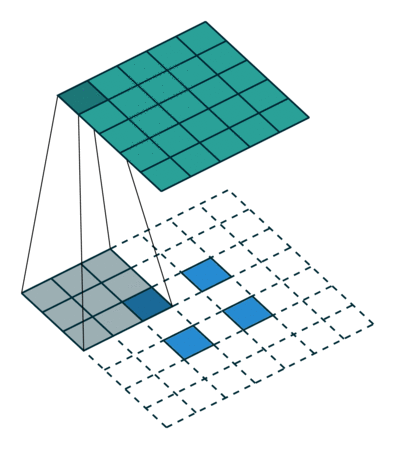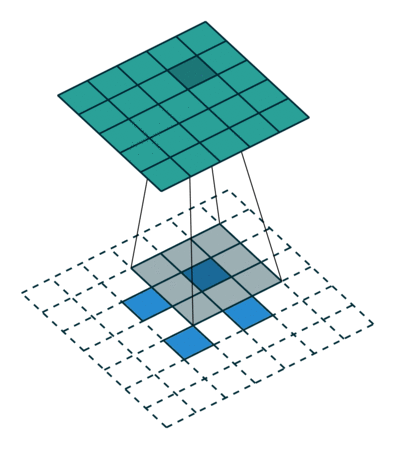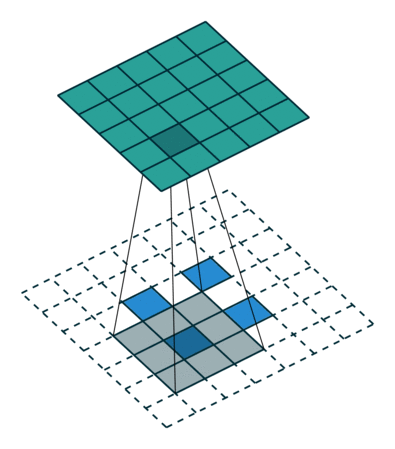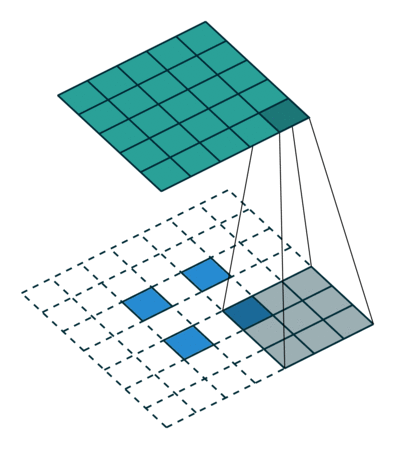
转置卷积(反卷积)

扩张卷积（空洞卷积）dilated convolution *

（1）标准的离散卷积
\[ (F * k)(\boldsymbol{p})=\sum_{\boldsymbol{s}+\boldsymbol{t}=\boldsymbol{p}} F(\boldsymbol{s}) k(\boldsymbol{t}) \]
扩张卷积

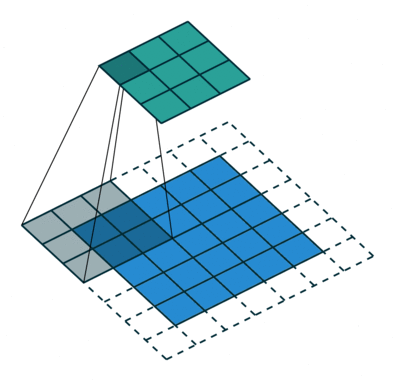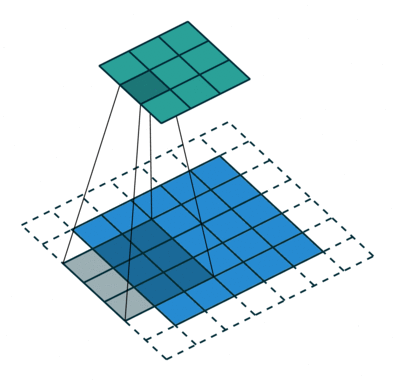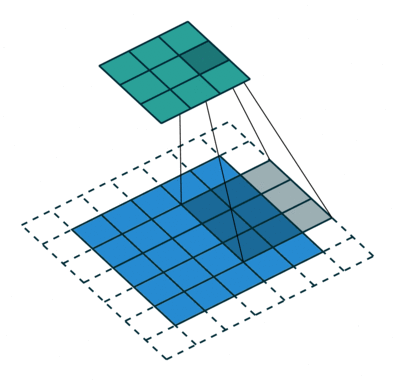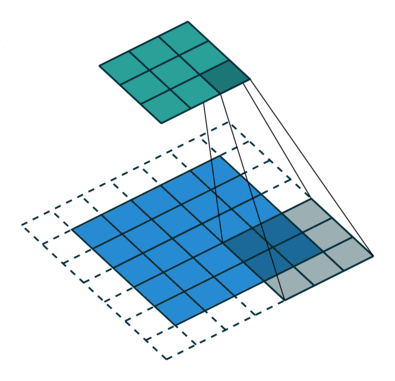
（2）扩张卷积如下：
\[ \left(F *_{l} k\right)(\boldsymbol{p})=\sum_{\boldsymbol{s}+l \boldsymbol{t}=\boldsymbol{p}} F(\boldsymbol{s}) k(\boldsymbol{t}) \]
当 l=1 时，扩张卷积会变得和标准卷积一样。

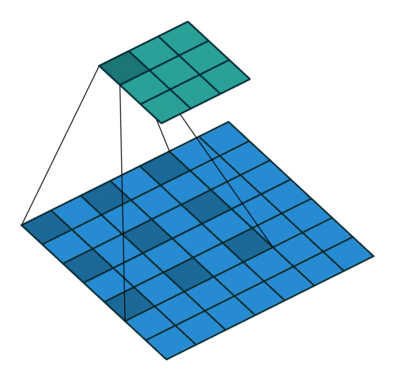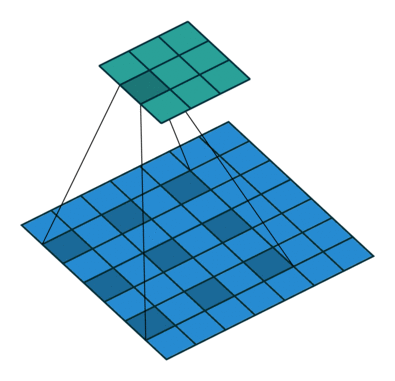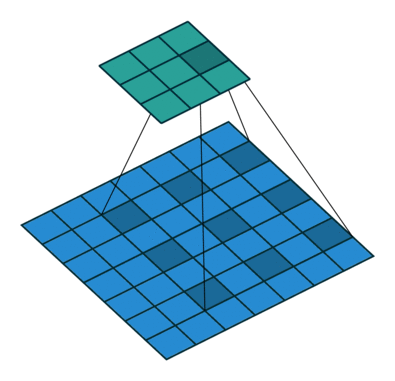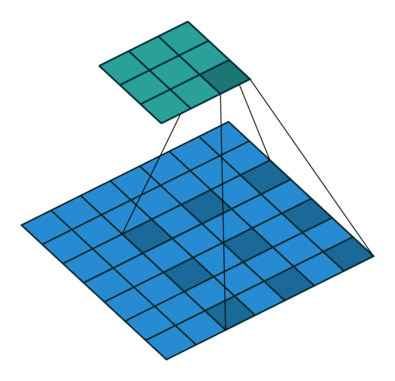
扩张卷积

直观而言，扩张卷积就是通过在核元素之间插入空格来使核「膨胀」。新增的参数 $l$（扩张率）表示我们希望将核加宽的程度。具体实现可能各不相同，但通常是在核元素之间插入 $l-1$ 个空格。下面展示了 $l = 1, 2, 4$ 时的核大小。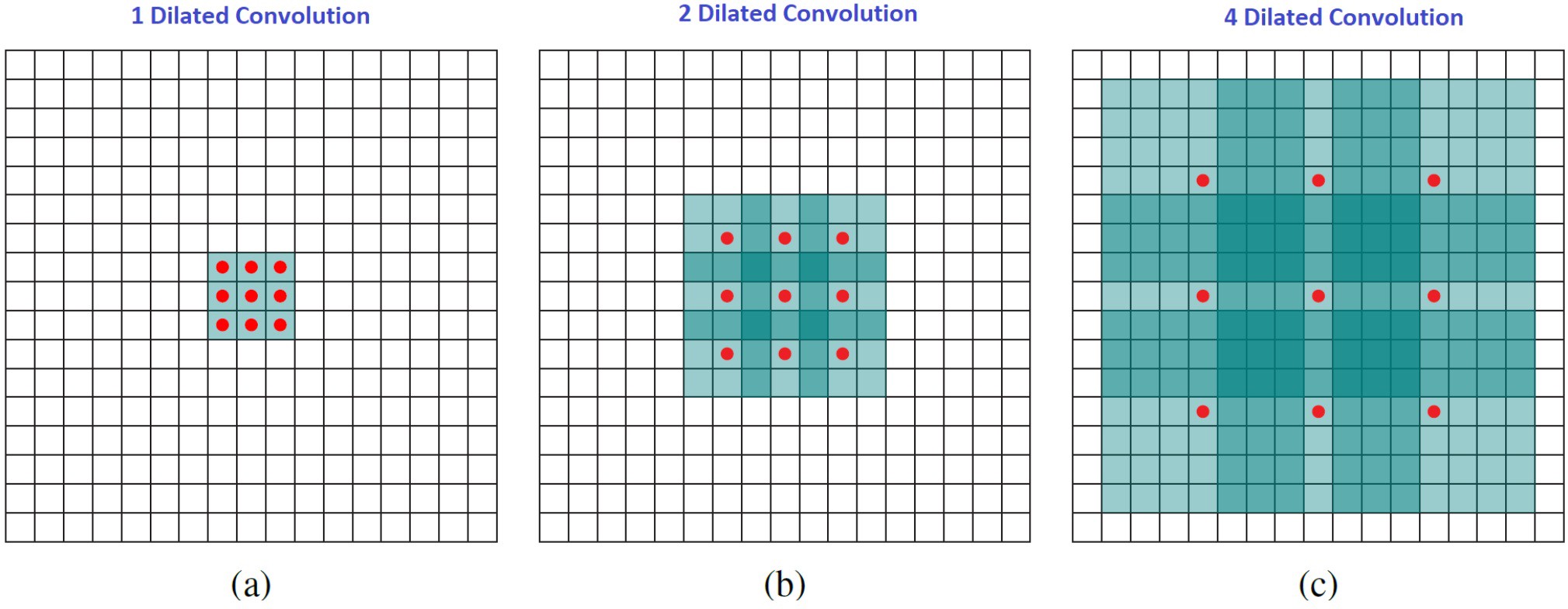扩张卷积的感受野。我们基本上无需添加额外的成本就能有较大的感受野

在这张图像中，3×3 的红点表示经过卷积后，输出图像是 3×3 像素。尽管所有这三个扩张卷积的输出都是同一尺寸，但模型观察到的感受野有很大的不同。$l=1$ 时感受野为 3×3，$l=2$ 时为 7×7。$l=3$ 时，感受野的大小就增加到了 15×15。有趣的是，与这些操作相关的参数的数量是相等的。我们「观察」更大的感受野不会有额外的成本。因此，扩张卷积可用于廉价地增大输出单元的感受野，而不会增大其核大小，这在多个扩张卷积彼此堆叠时尤其有效。

分组卷积(Group convolution)

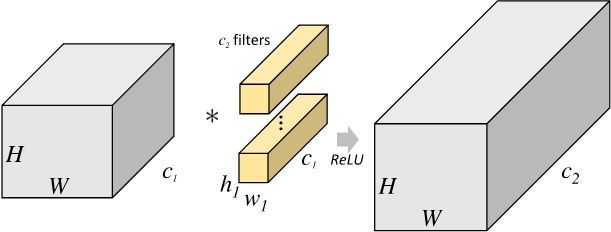
第一张图代表 标准卷积操作。若输入特征图尺寸为 $H \times W \times c_1$ ，卷积核尺寸为 $h_{1} \times w_{1} \times c_{1}$ ，输出特征图尺寸为 $H \times W \times c_{2}$ ，标准卷积层的参数量为： $\left(\boldsymbol{h}_{\mathbf{1}} \times \boldsymbol{w}_{\mathbf{1}} \times \boldsymbol{c}_{\mathbf{1}}\right) \times \boldsymbol{c}_{2}$ 。（一个滤波器在输入特征图 $h_{1} \times w_{1} \times c_{1}$ 大小的区域内操作，输出结果为1个数值，所以需要 $c_2$ 个滤波器。）

第二张图代表 分组卷积操作。将输入特征图按照通道数分成 $g$ 组，则每组输入特征图的尺寸为 $H \times W \times\left(\frac{c_{1}}{g}\right)$ ，对应的卷积核尺寸为 $h_{1} \times w_{1} \times\left(\frac{c_{1}}{g}\right)$ ，每组输出特征图尺寸为 $H \times W \times\left(\frac{c_{2}}{g}\right)$。将 $g$ 组结果拼接(concat)，得到最终尺寸为 $H \times W \times c_{2}$ 的输出特征图。分组卷积层的参数量为 $h_{1} \times w_{1} \times\left(\frac{c_{1}}{g}\right) \times\left(\frac{c_{2}}{g}\right) \times g=h_{1} \times w_{1} \times c_{1} \times c_{2} \times \frac{1}{g}$ 。

深入思考一下，常规卷积输出的特征图上，每一个点是由输入特征图 $h_{1} \times w_{1} \times c_{1}$ 个点计算得到的；而分组卷积输出的特征图上，每一个点是由输入特征图 $h_{1} \times w_{1} \times\left(\frac{c_{1}}{g}\right)$ 个点计算得到的。自然，分组卷积的参数量是标准卷积的 1$/ g$ 。

深度可分卷积(Depthwise separable convolution)

主要用于 MobileNet 和 Xception

这张图怎么少的了呢：

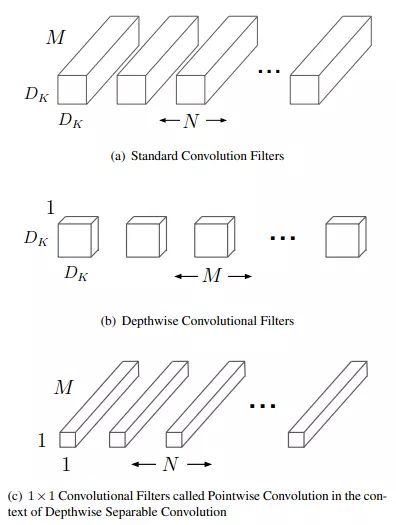
图(a)代表标准卷积。假设输入特征图尺寸为 $D_{F} \times D_{F} \times M$ ，卷积核尺寸为 $D_{K} \times D_{K} \times M$ ，输出特征图尺寸为 $D_{F} \times D_{F} \times N$，标准卷积层的参数量为： $\left(\boldsymbol{D}_{\boldsymbol{K}} \times \boldsymbol{D}_{\boldsymbol{K}} \times \boldsymbol{M}\right) \times \boldsymbol{N}$ 。

图(b)代表深度卷积，图(c)代表逐点卷积，两者合起来就是深度可分离卷积。深度卷积负责滤波，尺寸为 $(D_{K} , D_{K}, 1)$，共 $M$ 个，作用在输入的每个通道上；逐点卷积负责转换通道，尺寸为 $(1,1,M)$，共 $N$ 个，作用在深度卷积的输出特征映射上。

深度卷积参数量为 $\left(\boldsymbol{D}_{\boldsymbol{K}} \times \boldsymbol{D}_{\boldsymbol{K}} \times \mathbf{1}\right) \times \boldsymbol{M}$ ，逐点卷积参数量为 $(\mathbf{1} \times \mathbf{1} \times \boldsymbol{M}) \times \boldsymbol{N}$ ，所以深度可分离卷积参数量是标准卷积的 $\frac{D_{K} \times D_{K} \times M+M \times N}{D_{K} \times D_{K} \times M \times N}=\frac{1}{N}+\frac{1}{D_{K}^{2}}$ 。

为了便于理解、便于和分组卷积类比，假设 $M = N$ 。深度卷积其实就是 $g=M=N$ 的分组卷积，只不过没有直接将 $g$ 组结果拼接，所以深度卷积参数量是标准卷积的 1$/ N$ 。逐点卷积其实就是把 $g$ 组结果用 $1 \times 1$ conv 拼接起来，所以逐点卷积参数量是标准卷积的 1$/ D_{K}^{2}$ 。(只考虑逐点卷积，之前输出的特征图上每一个点是由输入特征图 $D_{K} \times D_{K}$ 区域内的点计算得到的；而逐点卷积输出上每一个点是由 $1 \times 1$ 区域内的点计算得到的)。自然，深度可分离卷积参数量是标准卷积的 $1 / N+1 / D_{K}^{2}$ 。

======================================================================================

深度可分离卷积由两步组成：深度卷积 和 1x1卷积

首先，在输入层上应用深度卷积。如下图，使用3个卷积核分别对输入层的3个通道作卷积计算，再堆叠在一起。

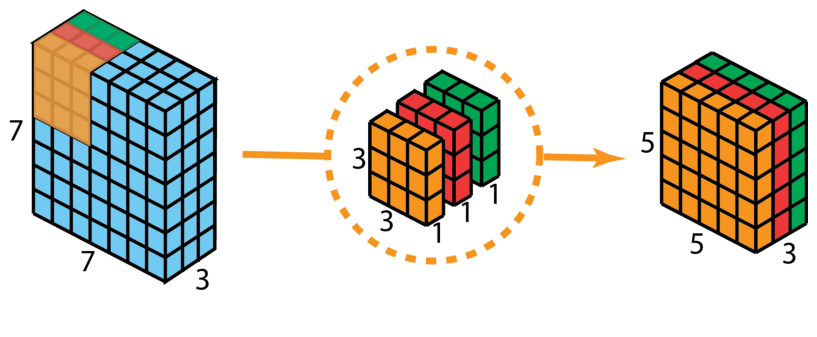
再使用1x1的卷积（3个通道）进行计算，得到只有1个通道的结果

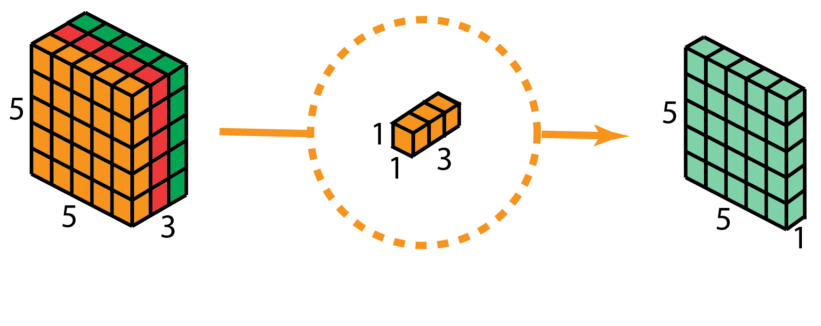
重复多次1x1的卷积操作（如下图为128次），则最后便会得到一个深度的卷积结果。

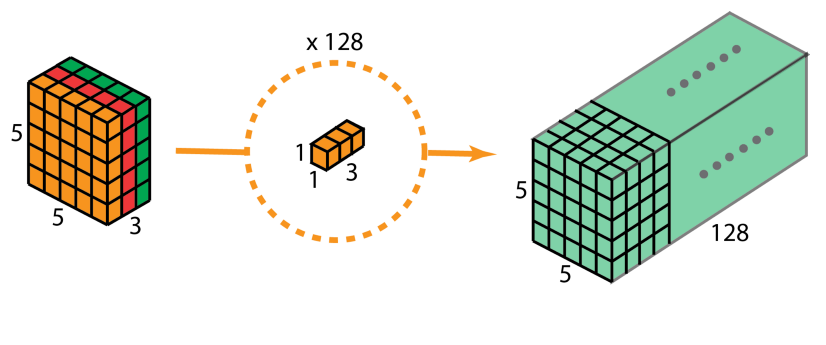
完整的过程如下：

卷积参数： 3 x 3 x 1 x 3 + 1 x 1 x 3 x 128 = $\frac{1}{C_{out}} + \frac{1}{K^2}$ = $\frac{1}{128} + \frac{1}{3 * 3}$

Reference: 1 2

空间可分卷积

主要思想是将卷积核拆分成两个更小的核，然后依次进行卷积，可以节省一部分成本，但深度学习却很少使用它。一大主要原因是并非所有的核都能分成两个更小的核。如果我们用空间可分卷积替代所有的传统卷积，那么我们就限制了自己在训练过程中搜索所有可能的核。这样得到的训练结果可能是次优的。（具体的有时间再补充）

感受野

感受野是卷积神经网络(CNN)每一层输出的特征图(feature map)上的像素点在原始输入图像上映射的区域大小。

感受野的计算

原始计算： $H_2 = \frac{H_1 - K + 2P}{S} + 1$

感受野计算：$H_1 = (H_2 - 1) * S + K - 2P$

增大感受野的方法
增加pooling层，但是会降低准确率
增大卷积核 kernel size，但是会增加参数
增加卷积层的个数，但是会面临梯度消失的问题
使用空洞卷积

1 2

Pooling层反向传播

1 . mean pooling

mean pooling的前向传播就是把一个patch中的值求取平均来做pooling，那么反向传播的过程也就是把某个元素的梯度等分为 $N$ 份分配给前一层，这样就保证池化前后的梯度（残差）之和保持不变，还是比较理解的，图示如下:

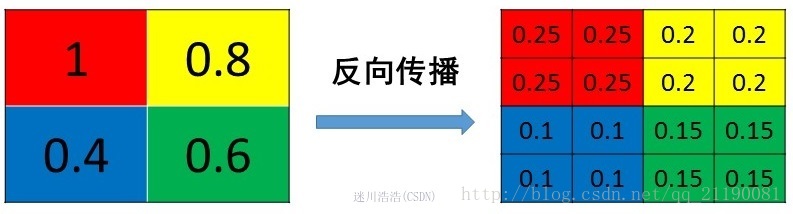
mean pooling比较容易让人理解错的地方就是会简单的认为直接把梯度复制 $N$ 遍之后直接反向传播回去，但是这样会造成loss之和变为原来的 $N$ 倍，网络是会产生梯度爆炸的。

2 . max pooling

首先考虑普通 max pooling 层如何求导，如何求导。设 $x_i$ 为输入层的节点，$y_j$ 为输出层的节点，那么损失函数 $L$ 对输入层节点 $x_i$ 的梯度为：
\[ \frac{\partial L}{\partial x_i} = \left\{ \begin{matrix} &0 &\delta(i,j) = false \\ &\frac{\partial L}{\partial y_j} &\delta(i,j) = true \end{matrix}\right. \]

其中判决函数 $δ(i,j)$ 表示 $i$ 节点是否被输出 $j$ 节点选为最大值输出。不被选中 $\delta(i,j) = false$ 有两种可能： $x_i$ 不在 $y_j$ 范围内，或者$x_i$ 不是最大值。

若选中，$\delta(i,j) = true$ ，则由链式法则可知：损失函数 $L$ 相对于 $x_i$ 的梯度 $\frac{\partial L}{\partial x_i}$ = $\frac{\partial L}{\partial y_i} \frac{\partial y_i}{\partial x_i}$ ，选中时 $\frac{\partial y_i}{\partial x_i} 恒等于1$
若不选中，$\delta(i,j) = false$ ，$\frac{\partial L}{\partial x_i}$ = $\frac{\partial L}{\partial y_i} \frac{\partial y_i}{\partial x_i}$ ，此时 $\frac{\partial y_i}{\partial x_i} 恒等于0$ ，综上可得上述公式

3 . roi max pooling

对于roi max pooling，设 $x_i$ 为输入层的节点，$y_{rj}$ 为第 $r$ 个候选区域的第 $j$ 个输出节点。一个输入节点可能和多个输出节点相连，如下图所示，输入节点7和两个候选区域输出节点相关连：

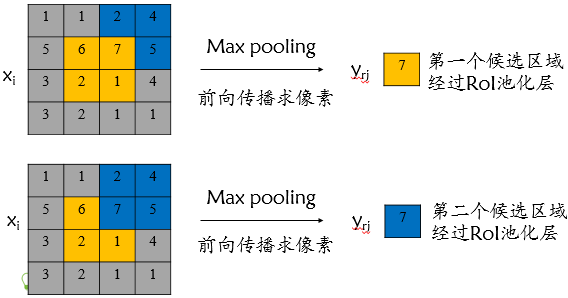
该输入节点7的反向传播如下图所示。对于不同候选区域，节点7都存在梯度，所以反向传播中损失函数 $L$ 对输入层节点 $x_i$ 的梯度为损失函数 $L$ 对各个有可能的候选区域 $r$ （ $x_i$ 被候选区域 $r$ 的第 $j$ 个输出节点选为最大值）输出 $y_{ri}$ 梯度的累加，具体如下公式所示：

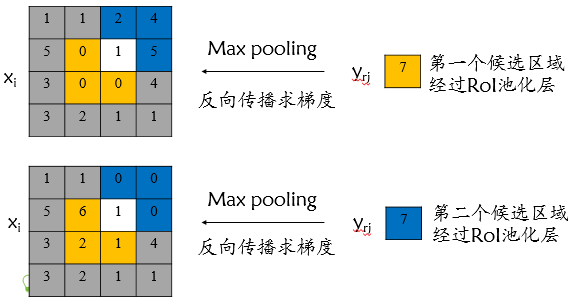
\[ \frac{\partial L}{\partial x_{i}}=\sum_{r} \sum_{j}\left[i=i^{*}(r, j)\right] \frac{\partial L}{\partial y_{rj}} \]

\[ \left[i=i^{*}(r, j)\right]=\left\{\begin{array}{ll}{1,} & {i=i^{*}(r, j) \geq 1} \\ {0,} & {\text { otherwise }}\end{array}\right. \]

判决函数 $[i=i^{*}(r, j)]$ 表示 $i$ 节点是否被候选区域 $r$ 的第 $j$ 个节点选为最大值输出。若是，则由链式规则可知损失函数 $L$ 相对 $x_i$ 的梯度等于损失函数 $L$ 相对 $y_{rj}$ 的梯度 ×（ $y_{rj}$ 对 $x_i$ 的梯度->恒等于1)，上图已然解释该输入节点可能会和不同的 $y_{rj}$ 有关系，故损失函数 $L$ 相对 $x_i$ 的梯度为求和形式。

为什么用SmoothL1 loss而不用 L2 loss

$Smooth_{L_1} Loss$ 对于离群点更加鲁棒，其相比于 $L2$ 损失函数，其对离群点，异常值(outlier)不敏感，可控制梯度的量级使训练时不容易跑飞，从梯度的角度进行分析。

https://www.zhihu.com/question/58200555

IOU

NMS

目标检测算法RCNN系列中，会从一张图片中找出n多个可能是物体的矩形框bounding box，每个矩形框都会有一个类别分类概率(得分)：

img

就像上面的图片一样，定位一个车辆，最后算法就找出了一堆的方框，我们需要判别哪些矩形框是没用的。

(1) 算法思想

按得分从低到高将 bbox 排序，例如：A、B、C、D、E、F

假设 F 的得分最高，保留。将A~E分别与F计算重叠度IoU，判断IoU是否大于某个设定的阈值。假设B、D与 F 的IoU大于阈值，那么B和D可认为是重复标记的，舍去。

余下A、C、E重复前面两步骤，找到所有被保留下来的bbox矩形框。

(2) 算法实现

python 实现：

1
2

MATLAB 实现：

function pick = nms(boxes, overlap)
% boxes: 	M x 5 表示有M个框，维度为5 [x1, y1, x2, y2, score]
% overlap:  IoU 阈值
if isempty(boxes)		% 输入为空，直接返回
  pick = [];
  return;
end

% 取出坐标与得分
x1 = boxes(:,1);	
y1 = boxes(:,2);
x2 = boxes(:,3);
y2 = boxes(:,4);
s = boxes(:,end);

% 计算每一个框的面积，并将得分按升序排列
area = (x2-x1+1) .* (y2-y1+1);
[vals, I] = sort(s);    

pick = s*0;
counter = 1;
% 循环直至所有框处理完
while ~isempty(I)       
  last = length(I);		% 当前剩余框的数量
  i = I(last);    		% 选中最后一个，即等分最高的框      
  pick(counter) = i;    % 每次保存得分最高的框
  counter = counter + 1;
  
  % 计算相交面积，画个图就面白坐标的意思
  xx1 = max(x1(i), x1(I(1:last-1)));
  yy1 = max(y1(i), y1(I(1:last-1)));
  xx2 = min(x2(i), x2(I(1:last-1)));
  yy2 = min(y2(i), y2(I(1:last-1)));
  
  w = max(0.0, xx2-xx1+1);
  h = max(0.0, yy2-yy1+1);
  inter = w.*h;
  
  % 不同定义下的IOU
  if strcmp(type,'Min')
  	% 重叠面积与最小框面积的比值
  	o = inter ./ min(area(i), area(I(1:last-1)));
  else
  	% 交集/并集
  	o = inter ./ (area(i) + area(I(1:last-1)) - inter);
  end
  
  % 保留所有重叠面积小于阈值的框，留作下次处理
  I = I(find(o<=overlap));
end

pick = pick(1:(counter-1));
end

C++ 实现

/**
 * @brief DetInference::NMS
 * @param bboxes:       Descend sorted bboxes
 * @param scores:       Descend sorted scores
 * @param overlap:      Overlap of NMS
 * @return              Remain bboxes' index
 */
std::vector<int> DetInference::NMS(std::vector<std::vector<float> > bboxes, std::vector<float> scores, float overlap) {
    std::vector<int> pick_vec;
    int n_sample = bboxes.size();
    std::vector<float> area_vec(n_sample);
    for (int i = 0; i < n_sample; i++) {
        area_vec[i] = (bboxes[i][2] - bboxes[i][0] + 1) * (bboxes[i][3] - bboxes[i][1] + 1);
        if (area_vec[i] < 0) {
            std::cout << "Boxes area must >= 0." << std::endl;
            return pick_vec;
        }
    }

    std::multimap<float, int> nms_score;
    for (int i = 0; i < n_sample; i++) {
        nms_score.insert(std::pair<float, int>(scores[i], i));  // Note: insert in position 0
    }

    do {
        int last = nms_score.rbegin()->second;
        pick_vec.push_back(last);

        // Get the biggest score map iterator for this literation, 
        // whose idx has save in pick_vec. And Then erase the max score map element.
        std::multimap<float, int>::iterator lit = nms_score.find(nms_score.rbegin()->first);
        nms_score.erase(lit);

        for (std::multimap<float, int>::iterator it = nms_score.begin(); it != nms_score.end(); ) {
            int it_idx = it->second;
            float xx1 = maxx(bboxes[last][0], bboxes[it_idx][0]);
            float yy1 = maxx(bboxes[last][1], bboxes[it_idx][1]);
            float xx2 = minn(bboxes[last][2], bboxes[it_idx][2]);
            float yy2 = minn(bboxes[last][3], bboxes[it_idx][3]);

            float w = maxx(float(0.0), xx2-xx1+1);
            float h = maxx(float(0.0), yy2-yy1+1);

            float ov = w * h / (area_vec[last] + area_vec[it_idx] - w * h + ESP);

            if (ov > overlap) {
                it = nms_score.erase(it);
            } else {
                it ++;
            }
        }
    } while (nms_score.size() != 0);
    return pick_vec;
}

Softmax 实现

卷积实现

Inception V1 - V4

总结

Inception V1

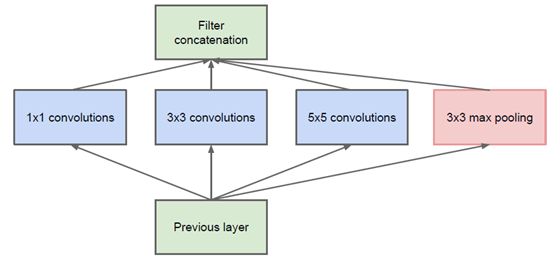
Inception-V1-0

将CNN中常用的卷积（1x1，3x3，5x5）、池化操作（3x3）堆叠在一起（卷积、池化后的尺寸相同，将通道相加），一方面增加了网络的宽度，另一方面也增加了网络对尺度的适应性。

然而这个Inception原始版本，所有的卷积核都在上一层的所有输出上来做，而那个5x5的卷积核所需的计算量就太大了，造成了特征图的厚度很大，为了避免这种情况，在3x3前、5x5前、max pooling后分别加上了1x1的卷积核，以起到了降低特征图厚度的作用，这也就形成了Inception v1的网络结构，如下图所示：

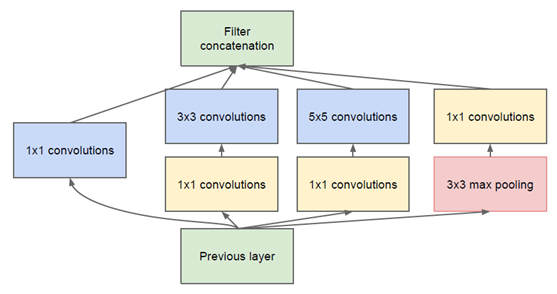
Inception-V1-1

Inception V2

（1）提出了卷积分解（Factorizing Convolutions）：学习 VGG 使用 两个3 X 3 的卷积核代替 5 X 5的卷积核，在保持感受野范围的同时又减少了参数量，并且还提高了网络的学习能力，引入了更多的ReLU非线性激活层。

（2）提出了 Batch Normalization，代替 Dropout 和 LRN，大大提升了网络的训练速度，同时收敛后的分类准确率也可以得到大幅提高，还一定程度上可以防止过拟合。

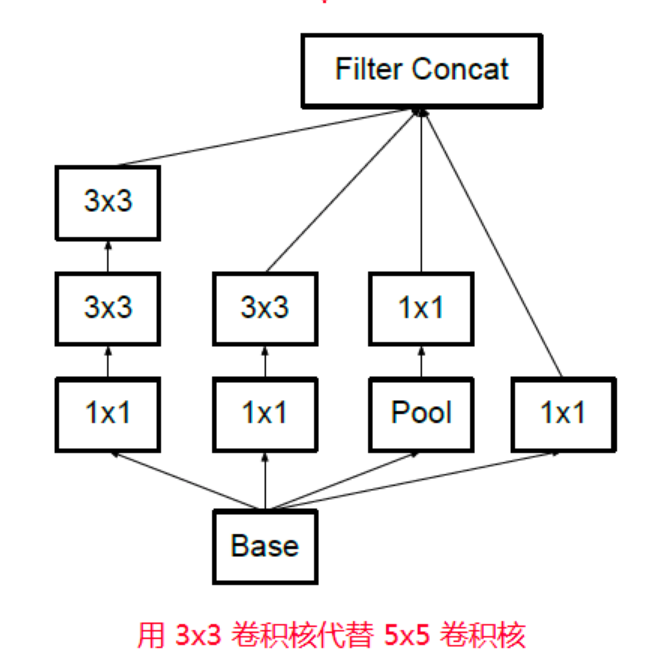
Inception-V2

Inception V3

引入了 分解 Factorization，将一个较大的二维卷积拆成两个较小的一维卷积，比如将3 X 3卷积拆成 1 X 3 卷积和 3 X 1 卷积，一方面节约了大量参数，加速运算并减轻了过拟合，同时增加了一层非线性扩展模型表达能力，除了在 Inception Module 中使用分支，还在分支中使用了分支（Network In Network In Network）

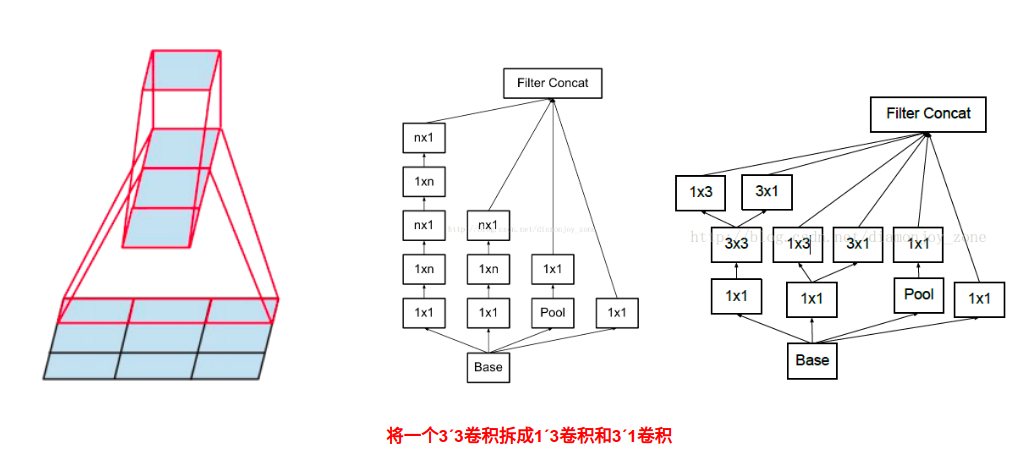
Inception-V3

Inception V4

研究了 Inception模块 与 残差连接 的结合，结合 ResNet 可以极大地加速训练，同时极大提升性能，在构建 Inception-ResNet 网络同时，还设计了一个更深更优化的 Inception v4 模型，能达到相媲美的性能。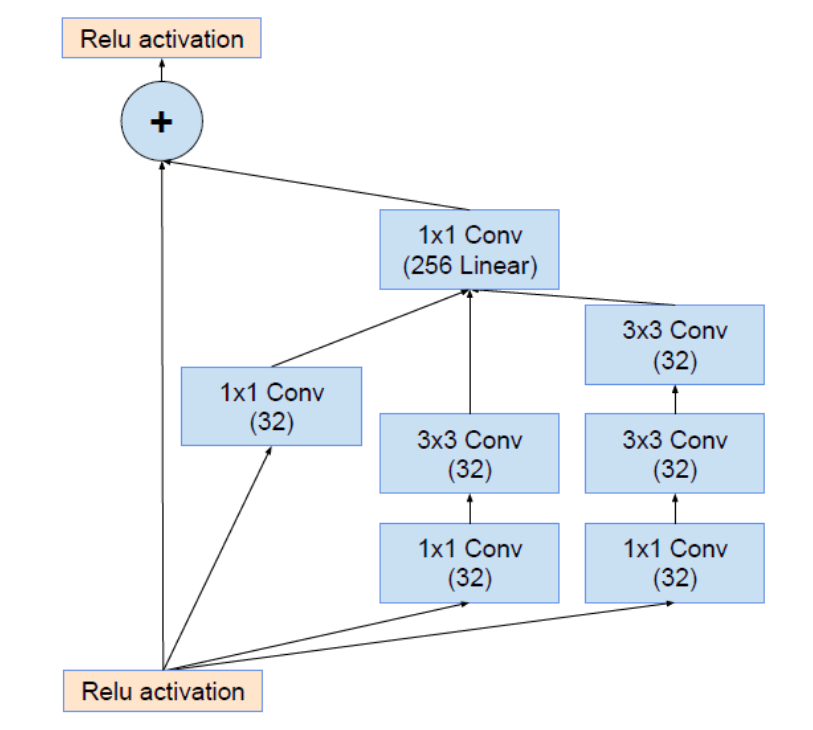 Inception-V4

Reference: 1

YOLO

工程部署

将模型提取出来，然后封装相应的C++接口，然后编写CUDA代码进行加速优化。

移动端部署 + 优化

数据结构

KMP算法

时间复杂度为： $O(n+m)$ ，朴素的模式匹配时间复杂度为：$O(n*m)$

（1）计算模式串的next数组方式

例题：在用KMP算法进行模式匹配时，求模式串 “ababaaababaa” 的next数组
next数组：中储存的是这个字符串前缀和后缀中相同字符串的最长长度，即模式串前面与后面匹配的位数，即为next的值

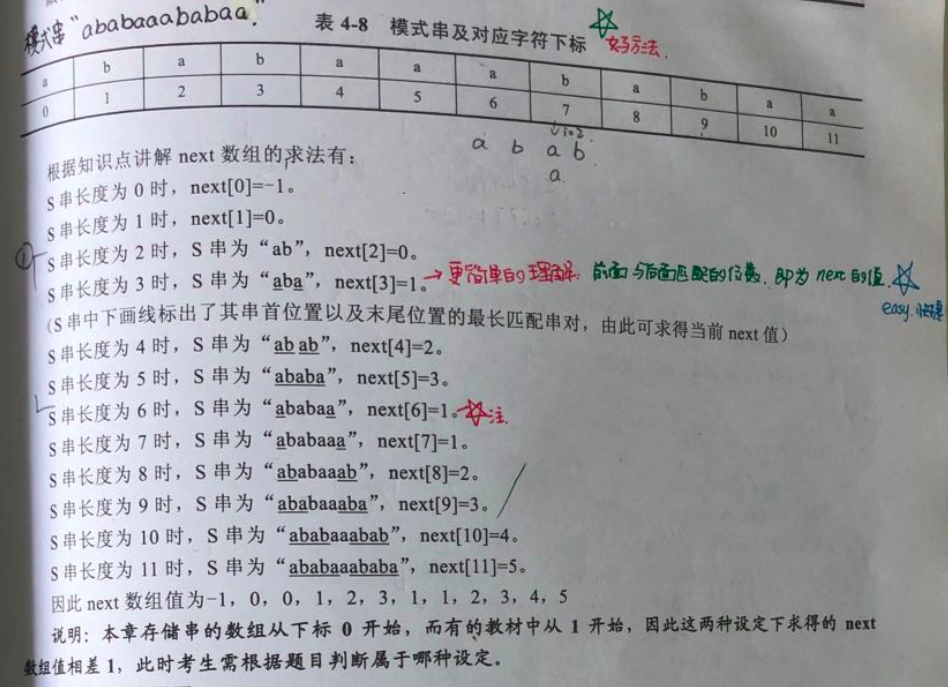
C++简单实现

#include <iostream>
#include <string>
using namespace std;

/**
 * KMP算法
 * @param str:      主串
 * @param substr:   模式串
 */ 
int KMP(string str, string substr, int next[]) {
    int i = 0, j = 0;
    while (i < str.length() && j < substr.length()) {
        if (j == -1 || str[i] == substr[j]) { // 字符匹配，或者j == -1，这个是由next数组产生的
            i++;
            j++;
        } else {                                // 字符不匹配
            j = next[j];
        }
    }
    if (j == substr.length())                   // 匹配成功，返回主串开始匹配的索引
        return i - substr.length();
    else                                        // 匹配不成功
        return -1;
}

/**
 * 计算模式串的next数组
 * @param substr:   模式串
 * @param next[]:   next数组
 * 思想：（自己手动结合md笔记例题好好Debug一遍就理解了）
 */ 
void GetNext(string substr, int next[]) {
    int i = 0, j = -1;
    next[0] = -1;
    while (i < substr.length()) {          
        if (j == -1 || substr[i] == substr[j]) {// 若 j==-1，或者该字符匹配时，则i,j都后移一位
            i++;
            j++;
            next[i] = j;
        } else {            // 若 j!=-1，或者该字符不匹配时，此时，substr[i]即与substr[next[j]]进行比较
            j = next[j];
        }
    }
}

int main() {
    string str = "ababababca";
    string strsub = "abababca";
    // 计算模式串的next数组
    int *next = new int[strsub.size()];
    GetNext(strsub, next);
    for (int i = 0; i < strsub.size(); i++) {
        cout << next[i];
    }
    cout << endl;

    // 使用KMP算法进行匹配
    int start_idx = KMP(str, strsub, next);
    int end_idx = start_idx + strsub.size();
    for (int i = start_idx; i < end_idx; i++) {
        cout << str[i];
    }
    cout << endl;
    delete [] next;
    return 0;
}

Python简单实现

def KMP(str, substr, next):
    """
    KMP 匹配算法
    :param str:     主串
    :param substr:  模式串
    :param next:    模式串的next数组
    :return:        返回匹配成功主串的起始匹配地址，或者不匹配时返回-1
    """
    i = 0
    j = 0
    while i < len(str) and j < len(strsub):
        if j == -1 or str[i] == strsub[j]:  # 字符匹配，或者j == -1，这个是由next数组产生的
            i += 1
            j += 1
        else:                               # 字符不匹配
            j = next[j]
    if j == len(substr):                    # 匹配成功，返回主串开始匹配的索引
        return i - len(substr)
    else:                                   # 匹配不成功
        return -1


def GetNext(substr, next):
    """
    计算模式串的next数组
    :param substr:  模式串
    :param next:    next数组，这里传入的是空的
    :return:        返回计算后的next数组
    """
    next[0] = -1
    i = 0
    j = -1
    while i < len(substr):          
        if j == -1 or substr[i] == substr[j]:
            i += 1
            j += 1
            next[i] = j
        else:
            j = next[j]
    return next


if __name__ == '__main__':
    str = "ababababca"
    strsub = "abababca"
    next = [0 for _ in range(len(strsub))]
    next = GetNext(strsub, next)
    start_idx = KMP(str, strsub, next)
    if start_idx == -1:
        print('字符串匹配失败')
    else:
        end_idx = start_idx + len(strsub)
    print(str[start_idx:end_idx])

几大排序算法

（1）时间复杂度

排序方法	平均时间	最好时间	最坏时间
桶排序($\color{red}不稳定$)	O(n)	O(n)	O(n)
基数排序($\color{green}稳定$)	O(n)	O(n)	O(n)
归并排序($\color{green}稳定$)	O(nlogn)	O(nlogn)	O(nlogn)
快速排序($\color{red}不稳定$)	O(nlogn)	O(nlogn)	O(n^2)
堆排序($\color{red}不稳定$)	O(nlogn)	O(nlogn)	O(nlogn)
希尔排序($\color{red}不稳定$)	O(n^1.25)
冒泡排序($\color{green}稳定$)	O(n^2)	O(n)	O(n^2)
选择排序($\color{red}不稳定$)	O(n^2)	O(n^2)	O(n^2)
直接插入排序($\color{green}稳定$)	O(n^2)	O(n)	O(n^2)

（2）空间复杂度

冒泡排序，简单选择排序，堆排序，直接插入排序，希尔排序的空间复杂度为 O(1)，因为需要一个临时变量来交换元素位置 (另外遍历序列时自然少不了用一个变量来做索引)

快速排序空间复杂度为 logn (因为递归调用了)，归并排序空间复杂是O(n)，需要一个大小为n的临时数组.

（3）最快的排序算法是桶排序

所有排序算法中最快的应该是桶排序(很多人误以为是快速排序,实际上不是.不过实际应用中快速排序用的多)但桶排序一般用的不多,因为有几个比较大的缺陷.

待排序的元素不能是负数,小数.
空间复杂度不确定,要看待排序元素中最大值是多少.

所需要的辅助数组大小即为最大元素的值.

归并排序会造成内存溢出，因为归并排序必须开额外的空间，而且空间开销还比较大。

题目 : 牛客

n个数值选出最大m个数（3<m<n）的最小算法复杂度是： $O(n)$

C++常见容器的时间复杂度

map ，set，multimap，multiset ：这4种容器是采用红黑树实现，红黑树是平衡二叉树的一种。不同操作的时间复杂度近似为:

插入：$O(logN)$
查找：$O(logN)$
删除：$O(logN)$

hash_map，hash_set，hash_multimap，hash_multiset：这4种容器采用哈希表实现。

插入：O(1)，最坏情况 O(N)
查找：O(1)，最坏情况 O(N)
删除：O(1)，最坏情况 O(N)

标准库提供的8个关联容器

map 和 set 的原理 *

map和set的底层实现主要通过 红黑树 来实现

红黑树是一种特殊的二叉查找树

1）每个结点要么是红的要么是黑的

2）根节点是黑色

3）每个叶子节点（叶结点即指树尾端NIL指针或NULL结点）是黑色

4）如果一个节点是红色的，则它的子节点必须是黑色的

5）对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点

特性4）5）决定了没有一条路径会比其他路径长出2倍，因此红黑树是接近平衡的二叉树。

正是红黑树的这5条性质，使一棵n个结点的红黑树始终保持了 $logn$ 的高度，从而也就解释了上面所说的 “红黑树” 的查找、插入、删除的时间复杂度最坏为 $O(log n)$

map 和 unordered_map 区别

map 是STL中的一个关联容器，提供键值对的数据管理。底层通过红黑树来实现，实际上是二叉排序树和非严格意义上的二叉平衡树。所以在map内部所有的数据都是有序的，且map的查询、插入、删除操作的时间复杂度都是 $O(logn)$

unordered_map 和 map 类似，都是存储 key-value 对，可以通过key快速索引到value，不同的是unordered_map不会根据 key 进行排序。unordered_map 底层是一个 防冗余的哈希表，存储时根据key的hash值判断元素是否相同，即 unoredered_map 内部是无序的。

二叉树分类

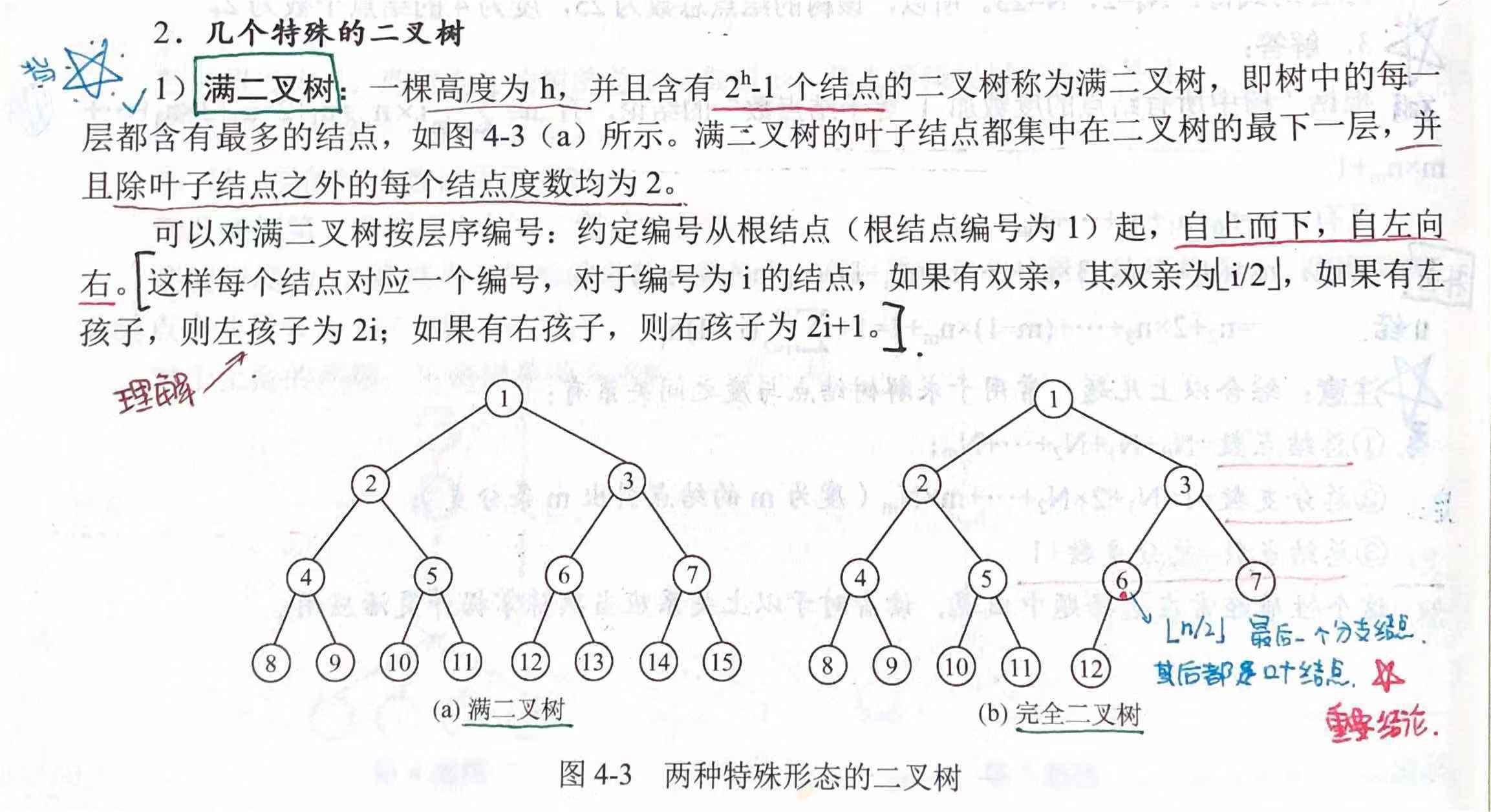
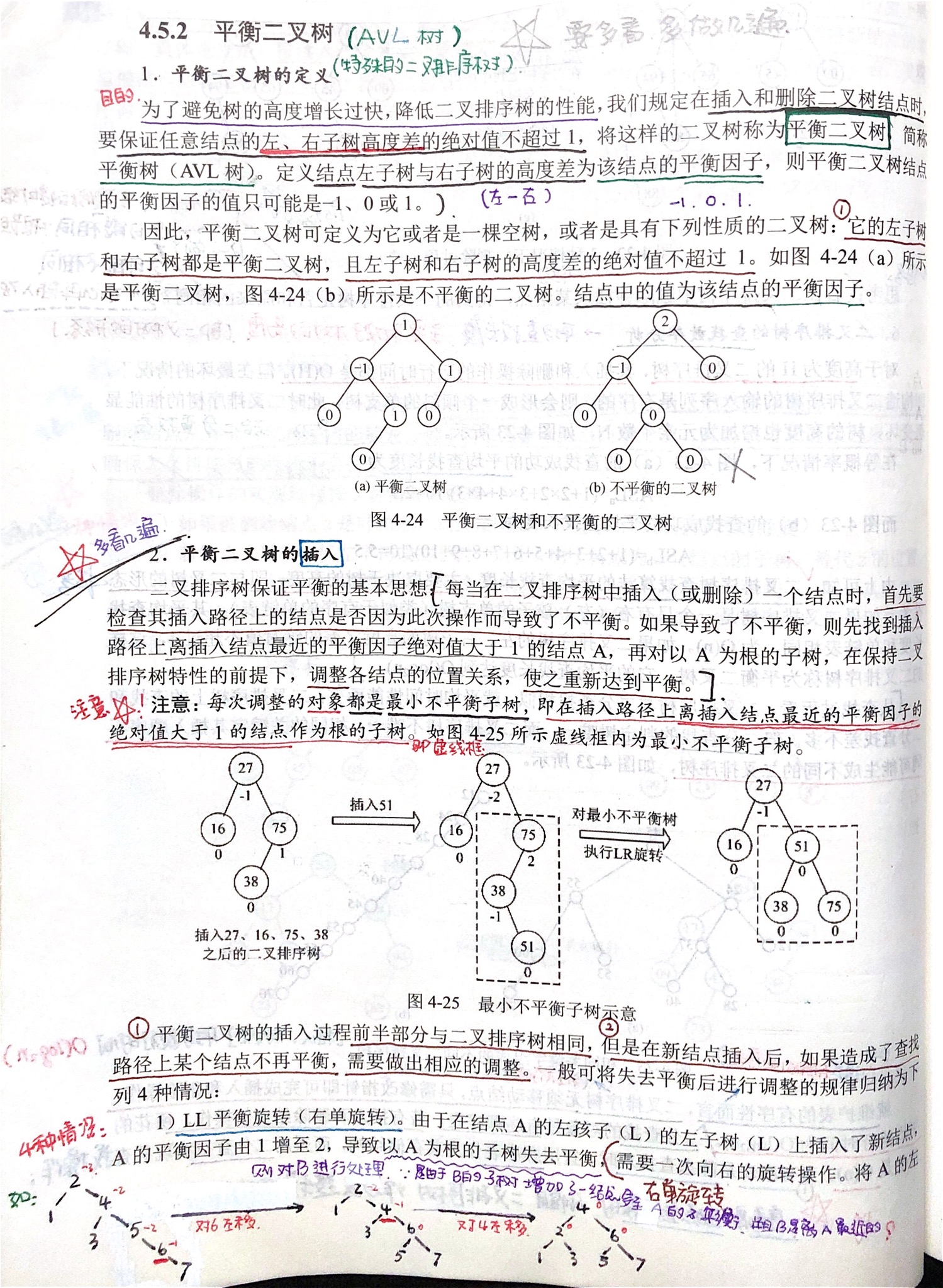
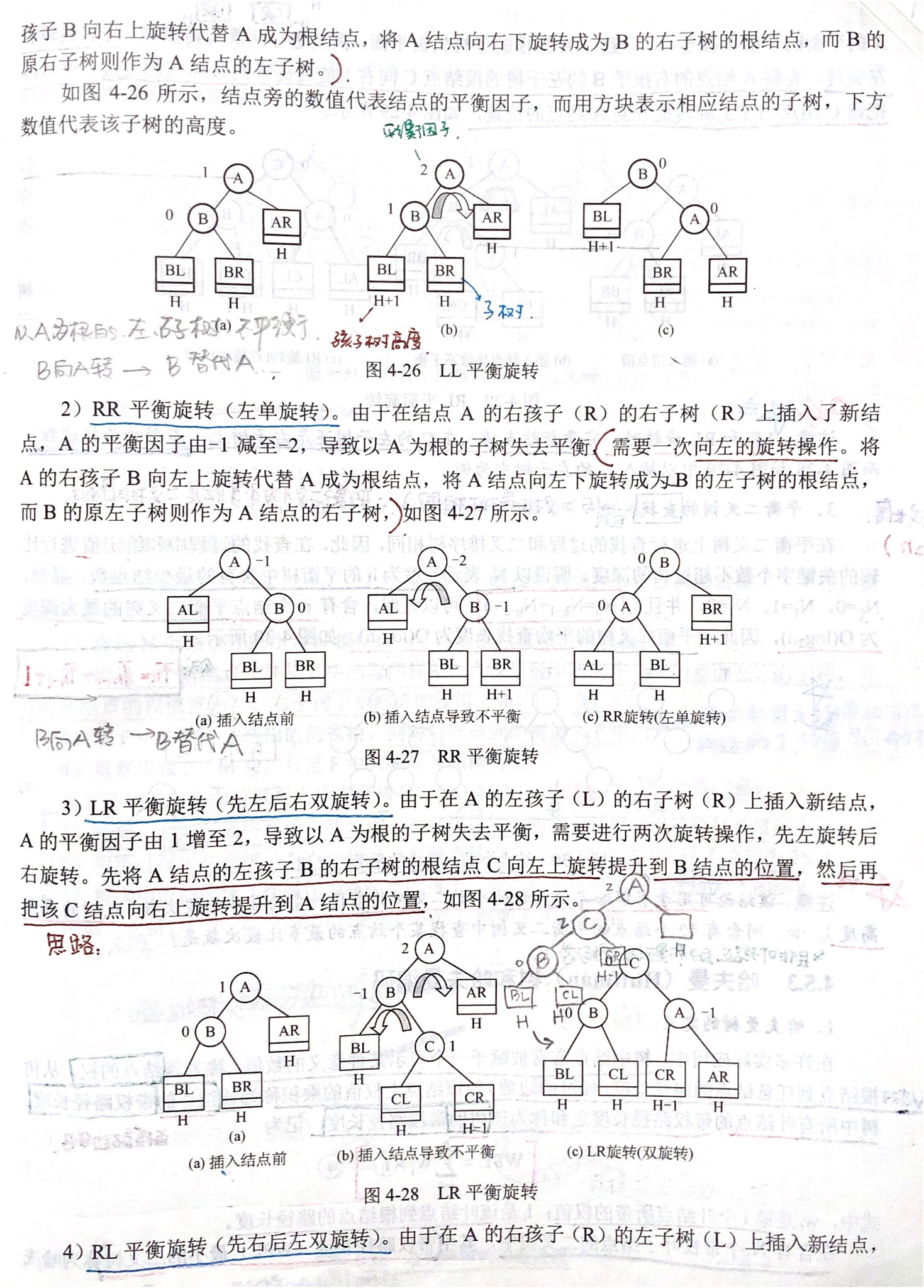
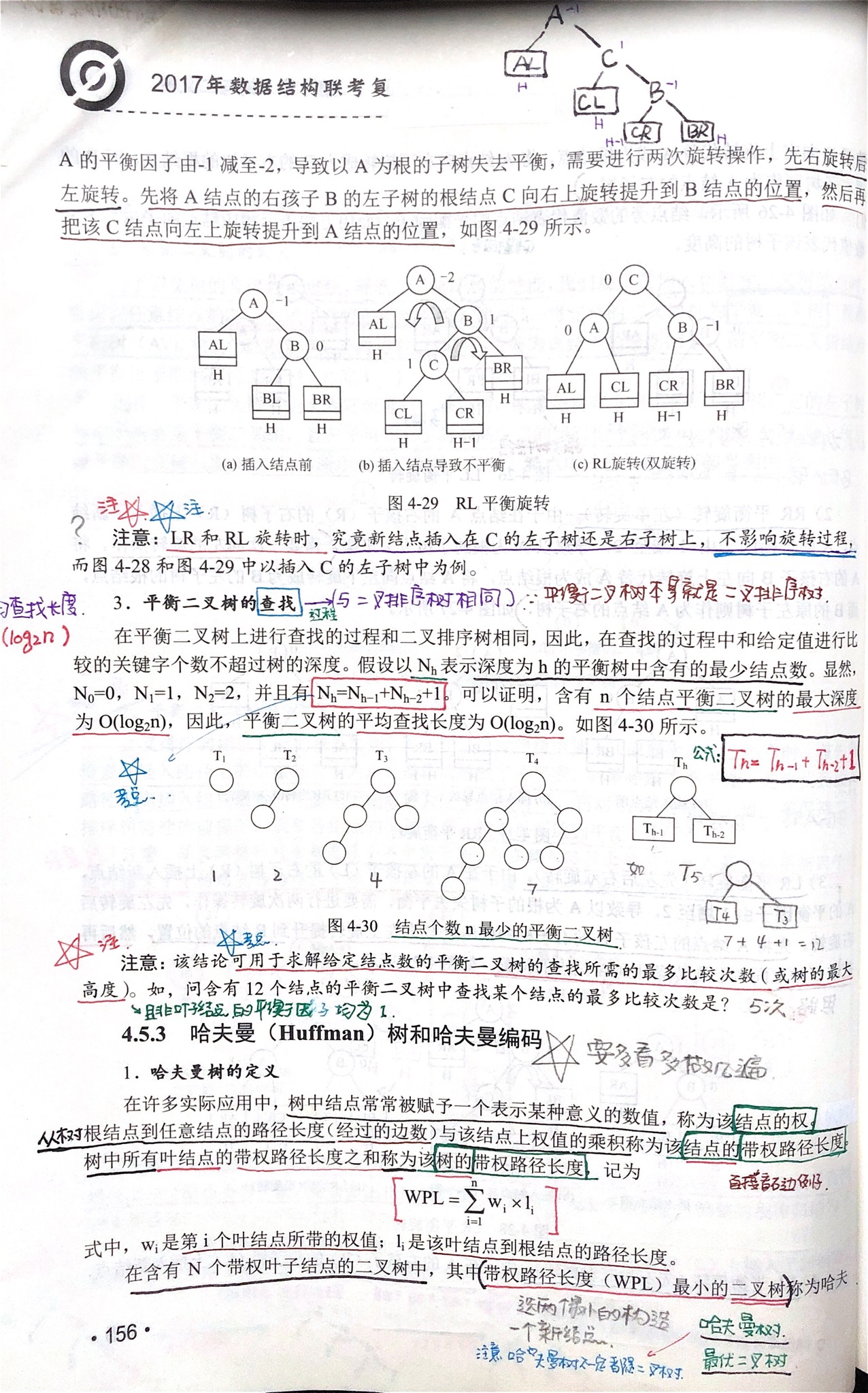
二叉查找(排序)树

二叉查找树，也称有序二叉树（ordered binary tree），或已排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值
若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值
任意节点的左、右子树也分别为二叉查找树
没有键值相等的节点（no duplicate nodes）

二叉排序数是一个递归的数据结构，可以很方便的使用递归算法对二叉排序树进行各种预算。由于 左子树节点值 < 根节点值 < 右子树节点值 ，所以可以通过中序遍历，得到一个递增的有序序列。

B 树和 B+树

1、B+树的层级更少：相较于B树B+每个非叶子节点存储的关键字数更多，树的层级更少所以查询数据更快；

2、B+树查询速度更稳定：B+所有关键字数据地址都存在叶子节点上，所以每次查找的次数都相同所以查询速度要比B树更稳定;

3、B+树天然具备排序功能：B+树所有的叶子节点数据构成了一个有序链表，在查询大小区间的数据时候更方便，数据紧密性很高，缓存的命中率也会比B树高。

4、B+树全节点遍历更快：B+树遍历整棵树只需要遍历所有的叶子节点即可，，而不需要像B树一样需要对每一层进行遍历，这有利于数据库做全表扫描。

B树相对于B+树的优点是，如果经常访问的数据离根节点很近，而B树的非叶子节点本身存有关键字其数据的地址，所以这种数据检索的时候会要比B+树快。

Reference: 1 2 3 4 5

面试题目

色彩空间，色彩空间的转换

膨胀与腐蚀

其是形态学最基本的两种操作。膨胀与腐蚀能实现多种多样的功能，主要如下：

消除噪声
分割(isolate)出独立的图像元素，在图像中连接(join)相邻的元素。
寻找图像中的明显的极大值区域或极小值区域
求出图像的梯度

膨胀和腐蚀是对白色部分（高亮部分）而言的，不是黑色部分。膨胀就是图像中的高亮部分进行膨胀，“领域扩张”，效果图拥有比原图更大的高亮区域。腐蚀就是原图中的高亮部分被腐蚀，“领域被蚕食”，效果图拥有比原图更小的高亮区域。

膨胀

膨胀就是求局部最大值的操作。按数学方面来说，膨胀操作就是将图像（或图像的一部分区域，我们称之为A）与核（我们称之为B）进行卷积。计算核B覆盖的区域的像素点的最大值，并把这个最大值赋值给参考点指定的像素。这样就会使图像中的高亮区域逐渐增长。

注意：其实右图要比左图大了一圈

效果图，高亮部分膨胀

膨胀数学公式：
\[ \operatorname{dst}(x, y)=\max _{\left(x^{\prime}, y^{\prime}\right) : \text { element }\left(x^{\prime}, y^{\prime}\right) \neq 0} \operatorname{src}\left(x+x^{\prime}, y+y^{\prime}\right) \]
用(x, y)周边区域(x+x', y+y')内的最大值代替(x, y)的值。

腐蚀

腐蚀与膨胀是相反的操作，腐蚀是求局部最小值。腐蚀操作就是将图像A与核B进行卷积。计算核B覆盖的区域的像素点的最小值，并把这个最小值赋值给参考点指定的像素。这样就会使图像中的高亮区域逐渐被腐蚀。

注意：其实右图要比左图小了一圈

A中能完全包含B的像素被留下来了。

效果图，高亮部分被腐蚀

边缘检测算子

边缘其实就是图像上灰度级变化很快的点的集合

主要可以通过计算梯度(连续函数中叫微分；图像是离散的，叫差分，意思是一样的，也是求变化率)

差分的定义：$f '(x) = f(x + 1) - f(x)$，用后一项减前一项。
按先后排列：$-f(x) + f(x + 1)$
提出系数 [-1, 1] 作为滤波模板，跟原图 $f(x)$ 做卷积运算就可以检测边缘了。

Roberts算子 *

Roberts算子是一种最简单的算子，是一种利用局部差分算子寻找边缘的算子。他采用对角线方向相邻两像素之差，来近似梯度幅值检测边缘。定位精度高，对噪声敏感，无法抑制噪声的影响。

具体公式：
\[ g(\mathrm{x}, \mathrm{y})= \sqrt{[\sqrt{f(x, y)}-\sqrt{f(x+1, y+1)}]^{2}+[\sqrt{f(x + 1, y)}-\sqrt{f(x, y + 1)} ]^{2}} \]
以上的 $f(x, y), f(x + 1, y), … $ 分别代表了图像中上下左右四个相邻像素：
\[ \begin{bmatrix} f(x, y) &f(x + 1, y) \\ f(x, y + 1) & f(x + 1, y + 1) \end{bmatrix} \]
下面的两个2x2的卷积核构成了 Roberts 算子
\[ g_x= \begin{bmatrix} 1 &0 \\ 0 &-1 \end{bmatrix} \ \ \ g_y= \begin{bmatrix} 0 &1 \\ -1 & 0 \end{bmatrix} \]
计算图像每个像素对应的梯度值：
\[ G_x = g_x * A \ \ \ \ and \ \ \ \ G_y = g_y * A \\ G = \sqrt{ {G_{x}}^2 +{G_y}^2} \]
以及梯度的方向：
\[ \Theta = arctan(\frac{G_y}{G_x}) \]
Prewitt算子

Prewitt 算子是加权平均算子，对噪声有抑制作用，但是像素平均相当于对图像进行的低通滤波，所以Prewitt 算子对边缘的定位不如 Robert 算子。

\[ \begin{bmatrix} f(x-1, y - 1) & f(x, y-1) &f(x+1, y-1) \\ f(x-1, y) &f(x, y) &f(x+1, y) \\ f(x-1, y+1) &f(x, y+1) &f(x+1, y+1) \\ \end{bmatrix} \]

$x$ 水平方向和 $y$ 垂直方向的算子分别为：
\[ g_x= \begin{bmatrix} -1 &0 & 1 \\ -1 &0 & 1 \\ -1 &0 & 1 \end{bmatrix} \ \ \ g_y= \begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{bmatrix} \]
Sobel算子（又称加权平均差分法）

Sobel算子和Prewitt算子都是加权平均，但是Sobel算子对于像素位置的影响作了加权，认为像素越近，影响越大。因此，效果也相对更好。

\[ G_x = \begin{bmatrix} -1 &0 &1 \\ -2 &0 &2 \\ -1 &0 &1 \end{bmatrix} * A \ \ \ \ and \ \ \ \ G_y = \begin{bmatrix} -1 &-2 &-1 \\ 0 &0 &0 \\ 1 &2 &1 \end{bmatrix} * A \]

然后再通过如下计算得到每个像素点对应的梯度值：
\[ G = \sqrt{ {G_{x}}^2 +{G_y}^2} \]
以及梯度的方向 [Compute gradient direction]：
\[ \Theta = arctan(\frac{G_y}{G_x}) \]

以上的算子都是利用一阶导数的信息，下面是利用二阶导数的边缘检测算子。

Laplace算子

Laplace算子是一种各向同性算子，二阶微分算子，具有旋转不变性。在只关心边缘的位置而不考虑其周围的象素灰度差值时比较合适。Laplace算子对孤立象素的响应要比对边缘或线的响应要更强烈，因此只适用于无噪声图象。
\[ \left[\begin{array}{ccc}{0} & {1} & {0} \\ {1} & {-4} & {1} \\ {0} & {1} & {0}\end{array}\right] \]
Canny算子

Canny算子是一个具有滤波，增强，检测的多阶段的优化算子，在进行处理前，Canny算子先利用高斯平滑滤波器来平滑图像以除去噪声，Canny分割算法采用一阶偏导的有限差分来计算梯度幅值和方向，在处理过程中，Canny算子还将经过一个非极大值抑制的过程，最后Canny算子还采用两个阈值来连接边缘。Canny边缘检测法利用高斯函数的一阶微分，它能在噪声抑制和边缘检测之间取得较好的平衡。

Canny边缘检测基本原理

1.高斯滤波器平滑图像，除去噪声。
2.一阶差分偏导计算梯度值和方向。
3.对梯度值不是极大值的地方进行抑制。
4.用双阈值连接图上的连通点。

算子	优缺点
Roberts	对具有陡峭的低噪声的图像处理效果较好，但提取的边缘结果较粗糙，边缘定位精度不是很高
Prewitt	对灰度渐变和噪声较多的图像处理较好，对噪声有一定的抑制，抑制的原理是通过像素平均，像素平均相当于对图像的低通滤波，所以定位不如Roberts
Soble	是对Prewitt的加权平均，认为不同距离的像素对当前像素的影响是不一样的，像素越近，影响越大。对灰度渐变和噪声较多的图像处理较好，对边缘定位比较准确
Lapacian	具有同向性，对图像中的阶跃性边缘定位准确，对噪声敏感，一般进行检测是要先滤波。但也会丢失一部分边缘方向信息，造成一些不连续的检测边缘
Candy	有好的信噪比，能够有效的抑制噪声，定位精度也高。

Reference: 1 2 3 4 5 6 7

典型例题：

下列关于图像边缘检测所用到的算子说法错误的是（B） A. Sobel算子是把各个方向上的灰度值加权之和作为输出 B. Robinson算子是一个边缘模板算子，由八个方向的样板组成，225度角模板为{2,1,0;1,2,-1;0,-1,-2} C. Kirsch算子是一个边缘模板算子，由八个方向的样板组成，255度角模板为{-3，-3，-3；5，0，-3,；5，5，-3} D. Prewitt算子是一个边缘模板算子，由八个方向的样板组成，255度角模板为 {-1,-1,1;-1,-2,1;1,1,1}

常见的特征点

Harris 角点：角点一般是对灰度图像或者二值图像进行处理，角点和边缘最大的区别就是角点在两个方向上都有较为剧烈的灰度变化，而边缘只在一个方向上有剧烈的灰度变化，如下图所示：

缺点：不具有尺度不变性

Sift (尺度不变特征变换，Scale-Invariant Feature Transform) 特征点：优势在于(尺度)缩放变换、平移变换和旋转变换的不变性，对光照变化、视角变化、仿射变换、噪声也保持一定程度的稳定性。缺点：计算量比较大，只利用了灰度性质算法，忽略了色彩信息。

SIFT算法的流程分别为：
(1) 尺度空间极点检测
(2) 关键点精确定位
(3) 关键点的方向确定
(4) 特征向量的生成

Reference: 1 2

Surf 特征点：是在Sift特征上进行的改进。主要特点是快速性，同时具有尺度不变性，对光照变化和仿射、透视变化也具有较强的鲁棒性。缺点：在求主方向阶段太依赖局部区域像素的梯度方向，有可能使得找到的主方向不准确。另外图像金字塔层取的不足够紧密也会使得尺度有误差。

Fast 特征点：主要检测局部像素灰度变化明显的地方，以速度快著称。它的思想是：如果一个像素与它邻域的像素差别较大（过亮或过暗） , 那它更可能是角点。相比于其他角点检测算法， FAST 只需比较像素亮度的大小，十分快捷。缺点：特征点数目很大且不缺定，并且Fast角点不具有方向信息。

ORB 特征点： 其是对FAST特征点与BREIF特征描述子的一种结合与改进，具体算法步骤如下：

利用FAST特征点检测的方法来检测特征点
利用Harris角点的度量方法，从FAST特征点从挑选出Harris角点响应值最大的N个特征点。

为FAST特征添加尺度不变性和旋转不变性，用BRIEF特征作为特征描述方法。速度最快，可用于实时性特征检测。

Reference : 特征匹配

随机洗牌法

蓄水池算法

Reference: 1 2

原理：直接先看代码！

假设数据序列的规模为 $n$，需要采样的数量的为 $k$
首先构建一个可容纳 $k$ 个元素的数组，将序列的前 $k$ 个元素放入数组中。
然后从第 $k+1$ 个元素开始，以 $k/j$ $(其中,j > k)$ 的概率来决定该元素是否被替换到数组中（数组中的元素被替换的概率是相同的）。当遍历完所有元素之后，数组中剩下的元素即为所需采取的样本。

证明

记忆：第m个元素被选中的概率为：$\frac{k}{m}$ （这里的 $ｍ$ 你可以替换成下面 $i, j$ 来理解）

（1）对于第 $i$ 个数（$i≤k$）。在 $k$ 步之前，被选中的概率为 1。当走到第 $k+1$ 步时，第 $i$ 个元素被 $k+1$ 个元素替换的概率 = $k+1$ 个元素被选中的概率 * $i$ 被选中替换的概率，即为 $\frac{k}{k+1} \times \frac{1}{k}=\frac{1}{k+1}$。则被保留的概率为 $1-\frac{1}{k+1}=\frac{k}{k+1}$。依次类推，不被 $k+2$ 个元素替换的概率为 $1-\frac{k}{k+2} \times \frac{1}{k}=\frac{k+1}{k+2}$ 。则运行到第 $n$ 步时，第 $i$ 个数被保留的概率 = 被选中的概率 * 不被替换的概率，即：
\[ 1 \times \frac{k}{k+1} \times \frac{k+1}{k+2} \times \frac{k+2}{k+3} \times \ldots \times \frac{n-1}{n}=\frac{k}{n} \]
（2）对于第 $j$ 个数（$j>k$）。在第 $j$ 步被选中的概率为 $\frac{k}{j}$，之后判断后面的数是否会替换该第 $j$ 个数。第 $j$ 个数不被 $j+1$ 个元素替换的概率为 $1-\frac{k}{j+1} \times \frac{1}{k}=\frac{j}{j+1}$。则运行到第 $n$ 步时，被保留的概率 = 被选中的概率 * 不被替换的概率，即：
\[ \frac{k}{j} \times \frac{j}{j+1} \times \frac{j+1}{j+2} \times \frac{j+2}{j+3} \times \ldots \times \frac{n-1}{n}=\frac{k}{n} \]
所以对于其中每个元素，被保留的概率都为 $\frac{k}{n}$

def reservoirSampling(seq, k):
    """
    蓄水池算法：先从 n 个元素中取前 k 个，然后对后面的(k+1 ~ n)个数，每个以 k / j 的概率替换前面的
    前 k 个数，这样我们得到的 k 个数就能保证是等概率 k / n 取出的
    (结合代码和笔记理解)
    :param seq: 长度为n的序列
    :param k:   int
    :return:    返回等概论取的 n 个序列
    """
    local_seq = copy.deepcopy(seq)  # 深拷贝
    n = len(local_seq)
    for j in range(k, n):           # 对后面的(n - k)个数，每次以（k / j）的概率的替换前k个数
        m = int(random.uniform(0, j))
        if m < k:
            temp = copy.deepcopy(local_seq[m])
            local_seq[m] = copy.deepcopy(local_seq[j])
            local_seq[j] = temp
    return local_seq[0:k]


if __name__ == '__main__':
    seq = [4, 5, 6, 3, 4, 7, 7, 4, 3, 3, 2, 4, 5, 5, 6, 9, 5, 4, 3, 45, 3, 23, 44, 55, 33, 5, 8]
    k = 5
    print(reservoirSampling(seq, k))

广义逆阵

关于矩阵的广义逆，下列表述不正确的是：

提出广义逆阵的原因

考虑以下的线性方程
\[ Ax = y \]
其中 $A$ 为 $n \times m$ 的矩阵，而 $y \in \mathcal{R}(A), A$ 的列空间。若矩阵 $A$ 为 $A$ 为可逆矩阵，则 $x = A^{-1}y$ 即为方程式的解。而若矩阵 $A$ 为可逆矩阵，则有：
\[ AA^{-1}A = A \]
假设矩阵 $A$ 不是可逆或是 $n \neq m$ ，需要一个合适的 $m \times n$ 矩阵 $G$ 使得下式成立：
\[ AGy = y \]
因为 $Gy$ 为线性系统 $Ax = y$ 的解。而同样的， $m \times n$ 的阶的矩阵 $G$ 也会使下式成立：
\[ AGA = A \]
因此可以用以下的方式定义广义逆阵：假设一个 $n \times m$ 的矩阵 $A$ ，$m \times n$ 的矩阵 $G$ 若可以使下式成立，矩阵 $G$ 即为 $A$ 的广义逆阵。
\[ AGA = A \]

产生广义逆阵

以下是一种产生广义逆阵的方式[3]：

若 $A=BC$ 为其秩分解，则 $G=C_{r}^{-}B_{l}^{-}$ 为 $A$ 的广义逆阵，其中 $C_{r}^{-}$ 为 $C$ 的右逆矩阵，而 $B_{l}^{-}$ 为 $B$ 的左逆矩阵。
若 $A=P{\begin{bmatrix}I_{r}&0\\0&0\end{bmatrix}}Q$ ，其中 $P$ 及 $Q$ 为可逆矩阵，则 $G=Q^{-1}{\begin{bmatrix}I_{r}&U\\W&V\end{bmatrix}}P^{-1}$ 是 $A$ 的广义逆阵，其中 $U,V$ 及 $W$ 均为任意矩阵。
令 $A$ 为秩为 $r$ 的矩阵，在不失一般性的情形下，令 $A={\begin{bmatrix}B&C\\D&E\end{bmatrix}}$ ，其中 $B_{r\times r}$ 为 $A$ 的可逆子矩阵，则 $G={\begin{bmatrix}B^{-1}&0\\0&0\end{bmatrix}}$ 为 $A$ 的广义逆阵。

广义逆阵的种类

彭若斯条件可以用来定义不同的广义逆阵：针对 $A \in \mathbb{R}^{n \times m} 及 A^{\mathrm{g}} \in \mathbb{R}^{m \times n}$ ，
\[ \begin{array}{l}{\text { 1.) } A A^{\mathrm{g}} A=A} \\ {\text { 2.) } A^{\mathrm{g}} A A^{\mathrm{g}}=A^{\mathrm{g}}} \\ {\text { 3.) }\left(A A^{\mathrm{g}}\right)^{\mathrm{T}}=A A^{\mathrm{g}}} \\ {\text { 4.) }\left(A^{\mathrm{g}} A\right)^{\mathrm{T}}=A^{\mathrm{g}} A}\end{array} \]
若 $A^{\mathrm{g}}$ 满足条件(1.)，即为 $A$ 的广义逆阵，若满足条件 (1.) 和 (2.)，则为 $A$ 的广义反身逆阵。若四个条件都满足，则为 $A$ 的摩尔－彭若斯广义逆。

海量数据处理问题

Reference: 0 1 2 4 3 5

一、top K问题

在大规模数据处理中，经常会遇到的一类问题：

从海量数据中找出最大的前k个数
或者在海量数据中找出出现频率最高的前k个数

这类问题通常被称为 top K问题。例如，在搜索引擎中，统计搜索最热门的10个查询词；在歌曲库中统计下载最高的前10首歌等。

处理方法

针对top K类问题，通常比较好的方案是：分治/hash映射 + Trie树/hash统计 + 小顶堆：说白了，就是 ${\color{red}先映射，而后统计，最后排序。}$
即先将数据集按照hash方法分解成多个小数据集，然后使用Trie树或者 hash统计每个小数据集中的query词频，之后用小顶堆求出每个数据集中出现频率最高的前K个数，最后在所有top K中求出最终的top K。

面试例题

(1) 10亿个数中找出最大的10000个数

先拿10000个数建小根堆，然后一次次添加剩余的元素，如果大于堆顶的数（10000中最小的），将这个数替换堆顶，并调整结构使之任然是一个小根堆，这样，遍历完后，堆中的10000个数就是所需的最大的10000个。构建堆时间复杂度是 $O(m)$ ，调整堆的时间复杂度为 $O(logm)$，所以总的时间复杂度为：1次建堆 + n 次调整 = $O(m + nlogm) = {\color{red}{O(nlogm)}}$（ $n$ 为10亿，$m$ 为10000）

优化方法：可以把所有10亿个数据分组存放，比如分别放在1000个文件中。这样处理就可以分别在每个文件的 $10^6$ 个数据中找出最大的10000个数，合并到一起在再找出最终的结果。
分治后再统计的时间复杂度依然是 $O(nlogm)$ = 1000个文件找每个文件的前10000个的时间复杂度 $O(1000 * 10^6log10000)$ + 加上1000个前10000个找最后的前10000个 $O(1000*10000*log10000)$ = $O(10^9log10000)$ = $O(nlogm)$

(2) 10亿个数中找出频率最高的10000个数

采用分治思想，先将10亿个数做hash求模映射到1000个小文件（$hash(x)$ % 1000 得到该数 $x$ 对应放在哪个文件 *），使用 $hash\_map$ 统计每个文件中各个数出现的频率，然后再使用小根堆的方法，求出每个小文件中出现频率最高的10000个，最后求出所有文件频率最高的10000个。

(3) 海量日志数据，提取出某日访问百度次数最多的那个IP

百度作为国内第一大搜索引擎，每天访问它的IP数量巨大，如果想一次性把所有IP数据装进内存处理，则内存容量明显不够，故针对数据太大，内存受限的情况，可以把大文件转化成（取模映射）小文件，从而大而化小，逐个处理。

分而治之/hash映射

首先把这一天访问百度日志的所有IP提取出来，然后逐个写入到一个大文件中，接着采用映射的方法，比如hash(IP) %1000，把整个大文件映射为1000个小文件，同一个IP在hash后，落在同一个文件中。

hash_map统计

然后使用hash_map(ip, value)来分别对1000个小文件中的IP进行频率统计，再找出每个小文件中出现频率最大的IP。

堆/快速排序

统计出最后1000个频率最大的IP后，依据各自频率的大小进行排序(可采取堆排序)，找出那个频率最大的IP，即为所求. 总共的时间复杂度为：$O(nlogm)$

(4) 有一千万个记录（这些查询串的重复度比较高，虽然总数是1千万，但如果除去重复后，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就是越热门），请你统计最热门的10个查询串，要求使用的内存不能超过1G

对于本题，数据规模比较小，能一次性装入内存，因为根据题目描述，虽然有一千万个Query，但是由于重复度比较高，故去除重复后，事实上只有300万的Query，每个Query255Byte，因此我们可以考虑把他们都放进内存中去（300万个字符串假设没有重复，都是最大长度，那么最多占用内存3M*1K/4=0.75G。所以可以将所有字符串都存放在内存中进行处理）

我们直接使用 hash_map(Query, Value) 进行统计，时间复杂度为O(n)，然后再使用之前的小根堆方式，得到频率最高的 10个查询串。时间负责度为 $O(10^6log10)$

(5) 有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词

顺序读文件中，对于每个词x，取hash(x)%5000，然后按照该值存到5000个小文件（记为x0,x1,…x4999）中。这样每个文件大概是200k左右。对超过1M的文件继续分割直到小于200K。使用hash_map统计各个词出现的频率，或者使用Trie数（时间复杂度为O(nle) :le为平均字符串长度）。对5000词使用堆排序或归并排序。

二、分布式 top K问题

(6) 分布在100台电脑的海量数据，统计前10

如果同一个数据元素只出现在某一台机器中

堆排序：在每台电脑上求出Top 10，构造包含10个元素的最小堆，然后同 (1)。
组合归并：然后将这100台电脑的Top 10组合起来，共1000个数据，再使用上面的方法求出 Top10即可，和上面说的都是一样的。

如果同一个元素重复出现在不同的电脑中
比如：第一台机器数据分布及各自出现的频率为：a(50)，b(50)，c(49)，d(49) ，e(0)，f(0)
第一台机器数据分布及各自出现的频率为：a(0)，b(0)，c(49)，d(49)，e(50)，f(50)

方法一：

遍历所有数据，重新hash取模，使同一个元素只出现在单独的一台电脑中，然后采用上面方法先统计每台电脑Top10再汇总起来求最终的Top10

方法二：

暴力求解：直接统计统计每台电脑中各个元素的出现次数，然后把同一个元素在不同机器中的出现次数相加，最终从所有数据中找出Top10

三、公共数据问题

(7) 给定a、b两个文件，各存放50亿个url，每个url各占64字节，内存限制是4G，让你找出a、b文件共同的url

可以估计每个文件的大小为5G×64=320G，远远大于内存限制的4G。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法。

分而治之/hash映射：遍历文件a，对每个url求取 hash(url)%1000，然后根据所取得的值将url分别存储到1000个小文件中（记为$a_0, a_1, ..., a_{999}$）这样每个小文件的大约为300M。遍历文件b，采取和a相同的方式将url分别存储到1000小文件中（记为 $b_0, b_1, ... , b_{999}$）。这样处理后，所有可能相同的url都在对应的小文件（ $a_{0}$ vs $b_{0}, a_{1}$ vs $b_{1}, \ldots, a_{0}$ vs $b_{999}$）中，不对应的小文件不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可。
hash_set统计：求每对小文件中相同的url时，可以把其中一个小文件的url存储到hash_set中。然后遍历另一个小文件的每个url，看其是否在刚才构建的hash_set中，如果是，那么就是共同的url，存到文件里面就可以了。

(8) 1000w有重字符串，对字符串去重

先hash分为多个文件
逐个文件检查并插入set中
多个set取交集

四、位图法

(9) 在2.5亿数字中找出不重复的整数

使用2-Bit位图法，00表示不存在，01表示出现一次，10表示出现多次，11无意义。这样共需要$2^{32} * 2$ = 1G 内存，还可以接受。然后扫描这2.5亿个整数，查看Bitmap中相对应位，如果是00变01，01变10，10保持不变。所描完事后，查看bitmap，把对应位是01的整数输出即可。
或者hash划分小文件，小文件使用hash_set检查各个元素，得到的。

(10) 给40亿个不重复的unsigned int的整数，没排过序的，然后再给一个数，如何快速判断这个数是否在那40亿个数当中？

位图法：申请 $2^{32} = 512M$ 的内存，一个bit位代表一个unsigned int值。读入40亿个数，设置相应的 bit位，读入要查询的数，查看相应 bit 位是否为1，为1表示存在，为0表示不存在。

五、Trie树

字典树、前缀树、单词查找树或键树。Trie树的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

基本性质

（1）根节点不包含字符，除根节点以外每个节点只包含一个字符。
（2）从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。
（3）每个节点的所有子节点包含的字符串不相同。

通常在实现的时候，会在节点结构中设置一个标志，用来标记该结点处是否构成一个单词（关键字）。Trie树的关键字一般都是字符串，而且Trie树把每个关键字保存在一条路径上，而不是一个结点中。

优点

（1）插入和查询的效率很高，都为O(m)，其中 m 是待插入/查询的字符串的长度。
（2）Trie树中不同的关键字不会产生冲突。
（3）Trie树只有在允许一个关键字关联多个值的情况下才有类似hash碰撞发生。
（4）Trie树可以对关键字按字典序排序。

缺点

（1）空间消耗比较大
（2）当 hash 函数很好时，Trie树的查找效率会低于哈希搜索

插入过程

对于一个单词，从根开始，沿着单词的各个字母所对应的树中的节点分支向下走，直到单词遍历完，将最后的节点exist 标记为 true，表示该单词已近插入Trie树。时间复杂度为 O(m)：m为单词长度

查找过程

同样的，从根开始按照单词的字母顺序向下遍历trie树，一旦发现某个节点标记不存在或者单词遍历完成而最后的节点未标记为exist=true，则表示该单词不存在，若最后的节点标记为exist=true，表示该单词存在。时间复杂度为 O(m)：m为单词长度

使用范围：

1 . 字符串检索

思路就是从根节点开始一个一个字符进行比较
（1）如果沿路比较，发现不同的字符，则表示该字符串不在该集合中。
（2）如果所有的字符全部比较完并且全部相同，还需判断最后一个节点的标志位（标记该节点是否代表一个关键字）。

struct trie_node {
    bool isKey;   // 标记该节点是否代表一个关键字
    trie_node *children[26]; // 各个子节点 
};

2 . 词频统计

思路：为了实现词频统计，我们修改了节点结构，用一个整型变量 count 来计数。对每一个关键字执行插入操作，若已存在，计数加1，若不存在，插入后 count 置1

struct trie_node {
    int count;   // 记录该节点代表的单词的个数
    trie_node *children[26]; // 各个子节点 
};

3 . 字符串排序

Trie树可以对大量字符串按字典序进行排序，思路也很简单：遍历一次所有关键字，将它们全部插入trie树，树的每个结点的所有儿子很显然地按照字母表排序，然后先序遍历输出Trie树中所有关键字即可。

4 . 前缀匹配

例如：找出一个字符串集合中所有以ab开头的字符串。我们只需要用所有字符串构造一个trie树，然后输出以a->b->开头的路径上的关键字即可。

trie树前缀匹配常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

问题实例

Reference: 1 2 3 4

面试算法题目

给定一个词典，和两个单词A, B. 每次只能改变一个字母，求A在词典中变换为B所需的最小次数
数组形式的a[i][j][k] 改用指针形式来访问
有序数组，旋转后查找一个数
判断一个数是不是2的指数次方的值

如果是2的倍数，那么该数的二进制位只有1位为1，所以只需要使用 n =  n & (n - 1) 即可，其可以掉最右边的一个1，若此时，n为0，则符合，否则，不符合。

最长公共子串 (商汤)

1
2

找到一个数组中唯一一个出现奇数次数的数（商汤）

1
2

给两个有序数组，求第3大的数（头条）

1
2

概率智力题

两个人拿金币，一次只能拿一个或者两个，最后拿光的人赢，怎样才能保证赢？

思想：这类题一般从后往前推，确定剩下多少个物品时，自己一定会赢，然后制定相应的策略。

假设总共有50块金币，A要获胜，就必须要保证他在倒数第二次拿到金币之后还剩下3个，这样无论B拿1个还是2个，最后一个都是A拿到。A要保证最后剩3个，则A需要第一拿金币后，剩下的金币是3的倍数，这样A可以控制每次A和B拿的金币之和为3，最后一定会剩下3个。所以50块金币，A只需刚开始拿2个，然后每次保证以后每次拿的个数与B拿的个数之和为3即可。

A、B两个人从一堆玻璃球（共100个）中向外拿球，规则如下：① A先拿，然后一人一次交替进行；② 每次只能拿1个、2个或者4个。③ 谁拿最后一个球，谁就是最后的失败者。请问，A、B两个人谁将是失败者？

和上一题类似，由于100 = 16*5+4，由于A先拿，B只要保证最后剩下的是1个或者4个，那么最后一个就一定是A拿。具体的策略是B要保证每次A和B拿玻璃球的个数之和为3个或者6个，这样B拿玻璃球之后剩下的玻璃球就是1个或者4个。所以A一定输。

有8瓶试剂，有一个有毒，用几只老鼠可以找出？

方法一：二分思想

每次把试剂分成两份[4, 4]，然后用两只老鼠来测试，试剂喝一小口就行，如果其中一只死掉了，就可以确定哪一堆有毒，然后继续将没毒的分成两份[2, 2]，用两只老鼠吃。8 = 2^3，所以只需要分3次，即3只老鼠就可以确定哪瓶试剂有毒。

方法二：位操作

8 = 2^3，按 _ _ _ 位来表示可以有8种状态。然后从低到高进行排列，用0-7表示8瓶试剂，3位中每位表示一个老鼠。
// [3, 2, 1]号老鼠
000 = 0 // 第0号试剂
001 = 1
010 = 2
011 = 3
100 = 4
101 = 5
110 = 6
111 = 7
然后我们每一列看，即按照每个老鼠看，比如：
1号老鼠，我们就将1、3、5、7号试剂混合给1号老鼠喝；
2号老鼠，我们就将2、3、6、7号试剂混合给2号老鼠喝；
3号老鼠，我们就将4、5、6、7号试剂混合给2号老鼠喝；
最后，如果1,3号老鼠死了，2号活着，我们对应找到101，即第5号试剂有毒（因为1,3号老鼠都吃了第5号试剂）。
如果1,2,3号老鼠都死了，则对应找到111，即7号试剂有毒。

注意，如果这里有时间限制，比如，吃了毒试剂要24小时后才会死，那么第一种方法则需要3天，第2种方法只需要1天即可

待整理

PCA 的两种解释
降为作用
另一种作用
SVM中的核函数有哪些
SVM中的核函数你用过么，存在的问题是什么
1000个样本，100维度，使用SVM计算内存占用情况
当数据的维度很大的，使用SVM会运行的很慢，你会如何处理
核函数的作用（自己要补充！）
核函数的引入避免了“维数灾难”，大大减小了计算量。
无需知道非线性变换函数Φ的形式和参数。
集成学习知道么

自己讲了一下 Boosting方法和Bagging方法

Kaggle比赛介绍一下
这种表格型比赛具体流程是怎么样的
错误错误结果如何分析
训练集和测试集如何划分的
介绍一下主流网络发展

矩阵相乘最小乘法次数

SVM 和 Softmax 区别

仿射变换和透视变化区别

透视变换矩阵的形状

SVM、LR 和 Softmax 区别

SVM寻参问题

SVM核函数解释

交叉熵损失可以用 L2损失替换么

先把YOLO看完（500问中有检测论文需要看的顺序）

简述 YOLO 和 SSD

YOLOv2

batch_size 和 learning rate的关系（怎么平衡和调整二者）

Inception v1-v4的演变

简述 CNN 的演变

ROI Pooling 和 ROI Align

CNN为什么有效 1 2

CNN在图像上表现好的原因

对迁移学习的理解，为什么能work

实现一个卷积操作 另一个简单实现卷积操作

模型精简加速

图像处理中的常用算子

卷积与反卷积

LSTM 与 RNN 模型

LSTM的结构，其相对于RNN的好处

BN原理与实战

面经集合

思维导图

https://www.nowcoder.com/discuss/242172?type=post&order=create&pos=&page=0

技术面：

1、自我介绍

2、项目介绍

3、互斥锁和条件变量如何实现线程同步，线程通信的方式

4、tcp/ip分层模型，tcp为什么是可靠的，如何实现可靠传输

5、内存泄漏，原因及解决方法

6、快排的实现

7、数据结构，map，set底层实现

8、c++的四个智能指针

9、描述一下输入url到页面返回的过程

HR面：

1、就业方向和就业地点

2、不是科班为什么选择互联网方向

2、职业规划

3、期望薪资

4、了解苏宁吗？这个比较尴尬（因为不太了解，感觉添的不行）

晚上8点-10点笔试

1、技术题，选择加问答，无编程

2、苏宁企业文化等

3、行测，言语理解与表达，资料分析，逻辑推理

https://www.nowcoder.com/discuss/244320?type=post&order=time&pos=&page=1

9.3下午苏宁数据挖掘算法管培生面试：

时间：近30min

形式：2V1，1技术官+1HR

整体总结：

面试比较水，只停留在简历的宏观层面（不知道对我不感兴趣，还是看我是妹子😂）。感觉面试官觉得我做的东西比较浅显，不大满意。有点小紧张，全程语速过快，该突出的点轻描淡写带过了，缺少深度、逻辑比较😂。9月底给通知。

一、技术面

. 自我介绍

. 重点介绍下项目，做了什么，怎么做的，具体用了什么技术/算法？

. 研究课题中具体使用了什么算法？

那些算法是我自己设计的，不是大家广知的，就简单带过了。说了数据预处理和聚类算法，真傻😂

. 在数据挖掘方面都了解什么算法？

我说了分类、聚类、关联规则、离群点检测。就问我离群点检测具体方法，额，我不知道…

. 了解哪些二分类算法？

. 说说贝叶斯算法思想？

HR面：

. 对苏宁有什么了解？

. 他们对苏宁有什么评价？

. 在苏宁的职业规划？

. 期望薪资是多少？

. 未来的定居计划？

. 都面了哪些公司？

. 你有什么想问我们的？

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
\(X^{(1)}\)	1	1	1	1	1	2	2	2	2	2	3	3	3	3	3
\(X^{(2)}\)	\(S\)	\(M\)	\(M\)	\(S\)	\(S\)	\(S\)	\(M\)	\(M\)	\(L\)	\(L\)	\(L\)	\(M\)	\(M\)	\(L\)	\(L\)
\(Y\)	-1	-1	1	1	-1	-1	-1	1	1	1	1	1	1	1	-1

排序方法	平均时间	最好时间	最坏时间
桶排序(\(\color{red}不稳定\))	O(n)	O(n)	O(n)
基数排序(\(\color{green}稳定\))	O(n)	O(n)	O(n)
归并排序(\(\color{green}稳定\))	O(nlogn)	O(nlogn)	O(nlogn)
快速排序(\(\color{red}不稳定\))	O(nlogn)	O(nlogn)	O(n^2)
堆排序(\(\color{red}不稳定\))	O(nlogn)	O(nlogn)	O(nlogn)
希尔排序(\(\color{red}不稳定\))	O(n^1.25)
冒泡排序(\(\color{green}稳定\))	O(n^2)	O(n)	O(n^2)
选择排序(\(\color{red}不稳定\))	O(n^2)	O(n^2)	O(n^2)
直接插入排序(\(\color{green}稳定\))	O(n^2)	O(n)	O(n^2)

模型评估

模型评估常用方法

机器学习中的Bias和Variance有什么区别和联系

经验误差与泛化误差

深度学习中的偏差与方差

偏差方差与Boosting和Bagging联系

偏差与方差的计算公式

偏差与方差的权衡（过拟合与模型复杂度的权衡）

欠拟合与过拟合

根据不同的坐标方式，图解欠拟合与过拟合

降低 过拟合 的方法

降低 欠拟合 的方法

L1/L2 范数正则化

L1/L2 范数的作用、异同

为什么 L1 和 L2 正则化可以防止过拟合？

为什么 L1 正则化可以产生稀疏权值，而 L2 不会？

交叉验证的主要作用

\(k\) 折交叉验证

Precision和Recall

P-R曲线

ROC与AUC

mAP

为什么要设置单一数字评估指标，设置指标的意义

训练/验证/测试集的定义及划分

什么是TOP5错误率

如何通过模型重新观察数据

有哪些改善模型的思路

激活函数

为什么需要激活函数？

为什么要使用非线性激活函数？

什么时候可以用线性激活函数

常见的激活函数

为什么Tanh收敛速度比Sigmoid快

怎样理解 ReLU（< 0 时）是非线性激活函数

损失函数/代价函数

为什么需要损失/代价函数

损失/代价函数的作用及原理

为什么损失/代价函数要非负

常用的损失函数

Softmax损失函数

Softmax-Loss损失函数

熵、条件熵、KL散度、交叉熵

为什么用交叉熵代替二次代价(均方误差)函数

范数

L-P范数

L0范数

L1范数

L2范数

L-∞范数

欧式距离 与 余弦相似度

线性回归

逻辑回归

回归划分

逻辑回归适用性

逻辑回归与朴素贝叶斯的区别

逻辑回归 与 线性回归 的联系与区别

逻辑回归 与 SVM 的联系与区别 *

逻辑回归 与 随机森林 区别

SVM

什么是支持向量

支持向量机的分类

最大间隔超平面背后的原理

支持向量机推导

一、线性可分支持向量机推导

SVM 标准问题的推导

SVM 对偶算法的推导

二、线性支持向量机

三、核函数

SVM为什么用对偶问题来求解

为何令间隔为1

什么是拉格朗日对偶

什么是KKT条件

* 反向传播

KNN

决策树

决策树的三要素

剪枝处理的作用及策略

决策树学习基本算法

[分类树] ID3 决策树与 C4.5 决策树

[回归树] - CART 决策树

降低过拟合的方法

降低欠拟合的方法

欧式距离与余弦相似度

逻辑回归与线性回归的联系与区别

逻辑回归与 SVM 的联系与区别 *

逻辑回归与随机森林区别

K值的选择手肘法

Boosting/Bagging 与偏差/方差的关系