Girshick, Ross. “Fast r-cnn.” Proceedings of the IEEE International Conference on Computer Vision. 2015.
继2014年的RCNN, SPP-Net,Ross Girshick在15年推出Fast RCNN,构思精巧,流程更为紧凑,大幅提升了目标检测的速度。在Github上提供了源码。
同样使用最大规模的网络,Fast RCNN和RCNN相比,训练时间从84小时减少为9.5小时,测试时间从47秒减少为0.32秒。在PASCAL VOC 2007上的准确率相差无几,约在66%-67%之间.
1. 思想
1.1 基础:R-CNN + SPP-Net
1.1.1 R-CNN
- R-CNN具有几个显著的缺点:
- 训练分为多个阶段,步骤繁琐 : 微调网络+训练SVM+训练边框回归器
- 训练耗时,占用磁盘空间大:5000张图像产生几百G的特征文件
- 速度慢:因为其要将每一张图片约2000个region proposals,都输入网络执行正向传递+SVM分类+边框回归,而不共享计算。其实际上对一张图像进行了约2000次提取特征和分类的过程。在使用GPU, VGG16模型处理一张图像需要47s。
(具体细节请看这篇博客)
1.1.2 SPP-Net
- SPP-Net利用sharing computation对 RCNN进行了加速:
- 提出一种将region proposals,映射到
conv5_3+relu5_3输出的feature map上的映射关系。只需要将一张图片输入网络,提取一次卷积层特征,然后通过这种映射关系,可将region proposals映射到对应的feature map上,即可获取每个region proposals的卷积特征。无需重复使用CNN提取特征,从而大幅度缩短训练时间。 由于FC层需要固定长度的输入,作者通过使用
SPP(Spatial Pyramid Pooling)层,可以接受任意大小的卷积特征向量,并输出固定长度的输出向量,就可以直接输入到FC层进行后续操作。即SPP-Net可接受任意大小的输入图片,不需要对图像做crop/wrap操作。
(即经过 映射+SPP转换 ,共享了计算,速度和精度都有一定提升) 具体细节请看这篇博客- SPP-Net 也有明显的缺点:
- 像R-CNN一样,训练分为多个阶段,步骤繁琐, : 微调网络+训练SVM+训练训练边框回归器
SPP-NET在微调网络的时候固定了卷积层,只对全连接层进行微调,而对于一个新的任务,有必要对卷积层也进行微调。(分类的模型提取的特征更注重高层语义,而目标检测任务除了语义信息还需要目标的位置信息)
针对以上两个问题,RBG提出了该Fast R-CNN,一个精简快速的检测框架。
1.2 改进:Fast RCNN
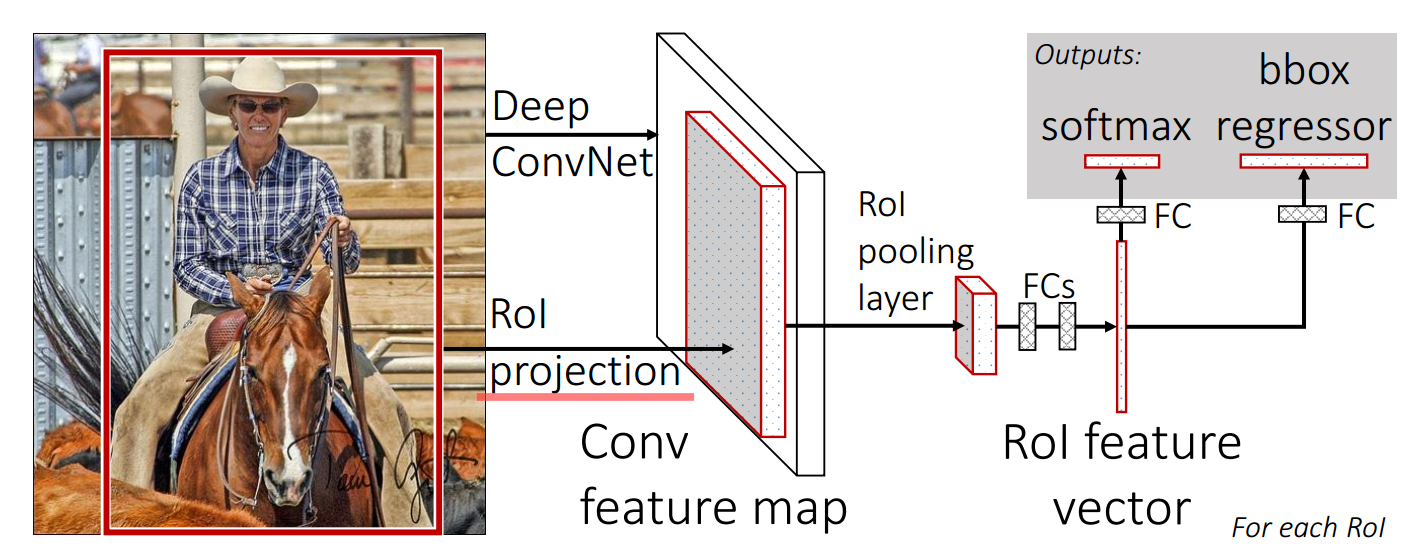
与R-CNN框架图对比,可以发现主要有两处不同:一是最后一个卷积层后加了一个ROI pooling layer,二是损失函数使用了多任务损失函数(multi-task loss),将边框回归直接加入到CNN网络中训练。
- ROI pooling layer实际上是SPP-Net的一个精简版,SPP-Net对每个proposal使用了不同大小的金字塔映射,而ROI pooling layer只需要下采样到一个7x7的特征图。对于VGG16网络conv5_3有512个特征图,这样所有region proposal对应了一个7x7x512维度的特征向量作为全连接层的输入。
- R-CNN训练过程分为了三个阶段,而Fast R-CNN直接使用softmax替代SVM分类,同时利用多任务损失函数边框回归也加入到了网络中,这样整个的训练过程是端到端的(除去region proposal提取阶段)。
- Fast R-CNN在网络微调的过程中,将部分卷积层也进行了微调,取得了更好的检测效果。
2. 特征提取网络
2.1 基本结构
图像归一化为224×224直接送入网络。
前五阶段是基础的 \(conv+relu+pooling\) 形式,在第五阶段结尾,输入P个候选区域(图像序号×1+几何位置×4,序号用于训练)?。
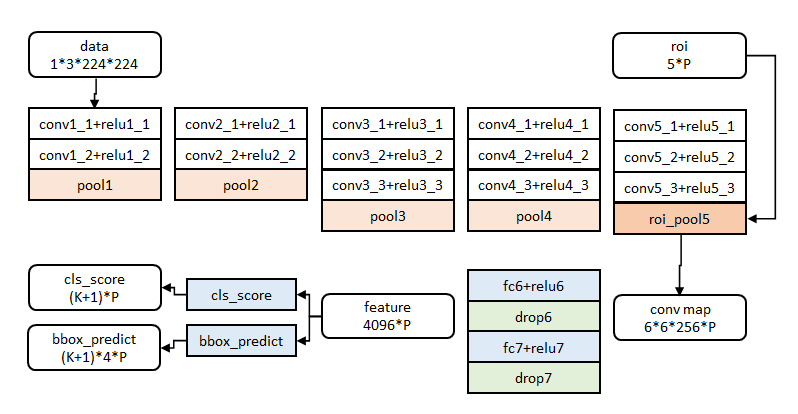
注:文中给出了大中小三种网络,此处示出最大的一种。三种网络基本结构相似,仅conv+relu层数有差别,或者增删了norm层。
2.2 roi_pool层的测试(forward)
roi_pool层将每个候选区域均匀分成M×N块,对每块进行max pooling。将特征图上大小不一的候选区域转变为大小统一的数据,送入下一层。
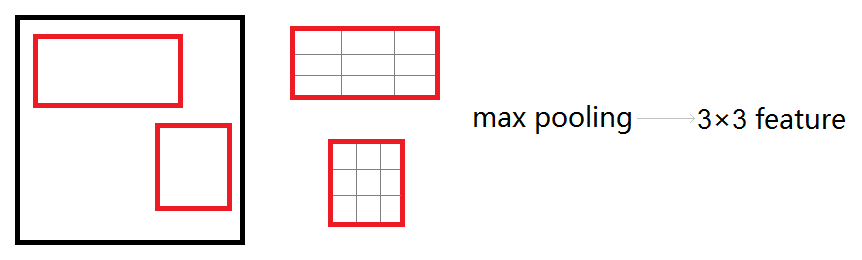
代码层理解:ROI Pooling层解析
2.3 roi_pool层的训练(backward)
首先考虑普通max pooling层如何求导,如何求导。设 \(x_i\) 为输入层的节点,\(y_j\) 为输出层的节点,那么损失函数 \(L\) 对输入层节点 \(x_i\) 的梯度为:
\[
\frac{\partial L}{\partial x_i} = \left\{
\begin{matrix}
&0 &\delta(i,j) = false \\
&\frac{\partial L}{\partial y_j} &\delta(i,j) = true
\end{matrix}\right.
\]
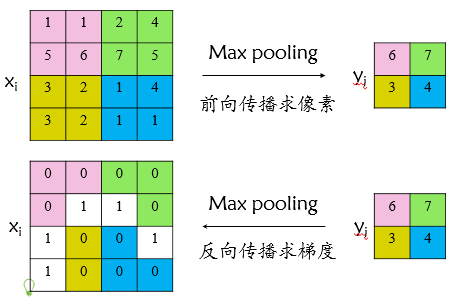
其中判决函数 \(δ(i,j)\) 表示 \(i\) 节点是否被输出 \(j\) 节点选为最大值输出。不被选中 \(\delta(i,j) = false\) 有两种可能: \(x_i\) 不在 \(y_j\) 范围内,或者\(x_i\) 不是最大值。
- 若选中,\(\delta(i,j) = true\) ,则由链式法则可知: 损失函数 \(L\) 相对于 \(x_i\) 的梯度 \(\frac{\partial L}{\partial x_i}\) = \(\frac{\partial L}{\partial y_i} \frac{\partial y_i}{\partial x_i}\) ,选中时 \(\frac{\partial y_i}{\partial x_i} 恒等于1\)
- 若不选中,\(\delta(i,j) = false\) ,\(\frac{\partial L}{\partial x_i}\) = \(\frac{\partial L}{\partial y_i} \frac{\partial y_i}{\partial x_i}\) ,此时 \(\frac{\partial y_i}{\partial x_i} 恒等于0\) ,综上可得上述公式
对于roi max pooling,设 \(x_i\) 为输入层的节点,\(y_{rj}\) 为第 \(r\) 个候选区域的第 \(j\) 个输出节点。 一个输入节点可能和多个输出节点相连,如下图所示,输入节点7和两个候选区域输出节点相关连:
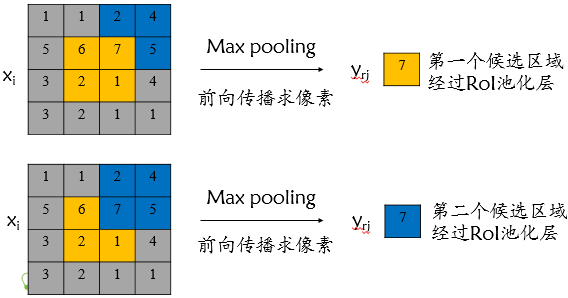
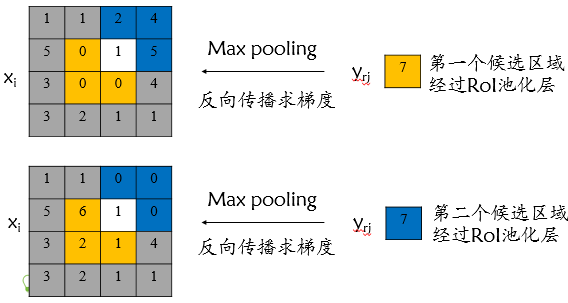
该输入节点7的反向传播如下图所示。对于不同候选区域,节点7都存在梯度,所以反向传播中损失函数 \(L\) 对输入层节点 \(x_i\) 的梯度为损失函数 \(L\) 对各个有可能的候选区域 \(r\) ( \(x_i\) 被候选区域 \(r\) 的第 \(j\) 个输出节点选为最大值)输出 \(y_{ri}\) 梯度的累加,具体如下公式所示:
\[
\frac{\partial L}{\partial x_{i}}=\sum_{r} \sum_{j}\left[i=i^{*}(r, j)\right] \frac{\partial L}{\partial y_{rj}}
\]
\[ \left[i=i^{*}(r, j)\right]=\left\{\begin{array}{ll}{1,} & {i=i^{*}(r, j) \geq 1} \\ {0,} & {\text { otherwise }}\end{array}\right. \]
判决函数 \([i=i^{*}(r, j)]\) 表示 \(i\) 节点是否被候选区域 \(r\) 的第 \(j\) 个节点选为最大值输出。若是,则由链式规则可知损失函数 \(L\) 相对 \(x_i\) 的梯度等于损失函数 \(L\) 相对 \(y_{rj}\) 的梯度 ×( \(y_{rj}\) 对 \(x_i\) 的梯度->恒等于1),上图已然解释该输入节点可能会和不同的 \(y_{rj}\) 有关系,故损失函数 \(L\) 相对 \(x_i\) 的梯度为求和形式。
3. 网络参数训练
3.1 参数初始化
网络除去末尾部分如下图,在ImageNet上训练1000类分类器。结果参数作为相应层的初始化参数。
其余参数随机初始化。
3.2 分层数据
在调优训练时,每一个mini-batch中首先加入N张完整图片,而后加入从N张图片中选取的R个候选框。这R个候选框可以复用N张图片前5个阶段的网络特征。
实际选择N=2, R=128。
3.3 训练数据构成
N张完整图片以50%概率水平翻转。
R个候选框的构成方式如下:
| 类别 | 比例 | 方式 |
|---|---|---|
| 前景 | 25% | 与某个真值重叠在[0.5, 1]的候选框 |
| 背景 | 75% | 与真值重叠的最大值在[0.1, 0.5)的候选框 |
4. 分类与位置调整
4.1 数据结构
第五阶段的特征输入到两个并行的全连层中(称为multi-task)。
cls_score层用于分类,输出K+1维数组 \(p\) ,表示属于K类和背景的概率。对每个RoI(Region of Interesting)输出离散型概率分布 $p = (p_0, p_1, …, p_k) $
bbox_predict层用于调整候选区域位置,输出bounding box回归的位移,输出4*K维数组 \(t\) ,表示分别属于K类时,应该平移缩放的参数。\(t^k = (t^k_x, \ t^k_y, \ t^k_w, \ t^k_h)\)
k表示类别的索引, \(t^k_x, \ t^k_y\) 是指相对于object proposal的ground truth尺度不变的平移, \(t^k_w, \ t^k_h\) 是指对数空间中相对于object proposal的ground truth的高与宽。
4.2 代价函数
loss_cls层评估分类代价。由真实分类 \(u\) 对应的概率决定:
\[
L_{cls} = - \ log{\ p_u}
\]
loss_bbox层评估检测框定位代价。比较真实分类对应的预测参数 \(t^u = (t^u_x, \ t^u_y, \ t^u_w, \ t^u_h)\) 和真实平移缩放参数为 \(v = (v_x, \ v_y \ , v_w, \ v_h)\) 的差别:
\[
L_{loc} = \sum_{i = 1}^4{g(t_i^u - v_i)}
\]
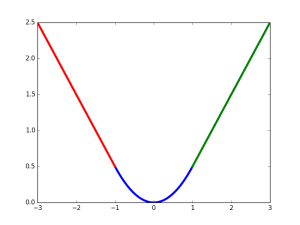
\(g\) 为\(Smooth L1\)误差,函数图像如下,其在(-1, 1)之间为二次函数,其他区域为线性函数。作者这样设置的目的是想让loss对于离群点更加鲁棒,相比于 \(L2\) 损失函数,其对离群点,异常值(outlier)不敏感,可控制梯度的量级使训练时不容易跑飞。
\[
g(x) = \left\{
\begin{eqnarray}
&&0.5x^2 \ \ \ &|x| < 1 \\
&&|x| - 0.5 \ \ \ & otherwise
\end{eqnarray}\right.
\]
总代价为两者加权和,如果分类为背景则不考虑定位代价:
\[
L = \left\{
\begin{eqnarray}
&&L_{cls} + \lambda L_{loc} \ & u为前景 \\
&&L_{cls} \ & u为背景
\end{eqnarray}\right.
\]
规定 \(u=0\) 为背景类(也就是负标签),那么艾弗森括号指数函数 \([u≥1]\) 表示背景候选区域即负样本不参与回归损失,不需要对候选区域进行回归操作。\(λ\) 控制分类损失和回归损失的平衡。Fast R-CNN论文中,所有实验\(λ=1\)。
艾弗森括号指数函数为:
\[
[u \ge 1] =\begin{cases}1 & u \ge 1 \\ 0 & otherwise\end{cases}
\]
源码中几个参数说明:
cls_score: cls_score分类层的输出结果,CNN计算的每个rois (bbox)属于[K类前景+1背景]的概率得分。 [1x(K+1)]
label: 原始输入的每个rois所属的类别标签。 [1*1]
bbox_pred: bbox_prdict层输出的,CNN计算的每个rois预测需要进行bounding box回归的平移缩放参数。[1x4x(K+1)] (注意,这是源码中的维度,上图中的写成了维度[1x4]是为了易于理解损失loss的计算)
bbox_targets: 使用原始数据rois和ground truth计算好了的,每个前景rois回归到其对应的ground truth所需要做的平移尺度变换,背景不需要bounding box回归,对应的值为0。 [1x4x(K+1)]
bbox_loss_weights: 标记每个rois是否属于某一个类。 [1x4x(K+1)]:属于的类别4个位置标志为1,不属于的为都为0
overlap: (每个[ground truth + region proposals] (boxes)与每个ground truth的重叠率[若一个boxes与同类的多个ground truth重叠率取最大的那个])
4.3 全连接层提速
分类和位置调整都是通过全连接层(fc)实现的,设前一级数据为 \(x\) 后一级为 \(y\) ,全连接层参数为 \(W\) ,尺寸\(u×v\) 。一次前向传播(forward)即为:
\[
y=Wx
\]
计算复杂度为 \(u×v\)
将\(W\)进行SVD分解,并用前t个特征值近似:
\[
W=UΣV^T≈U(:,1:t)⋅Σ(1:t,1:t)⋅V(:,1:t)^T
\]
原来的前向传播分解成两步:
\[
y=Wx=U⋅(Σ⋅V^T)⋅x=U⋅z
\]
计算复杂度变为 \(u×t+v×t\) (这部分不是很理解?)
在实现时,相当于把一个全连接层拆分成两个,中间以一个低维数据相连。
在github的源码中,这部分似乎没有实现。
5. 实验与结论
实验过程不再详述,只记录结论
- 网络末端同步训练的分类和位置调整,提升准确度
- 使用多尺度的图像金字塔,性能几乎没有提高
- 倍增训练数据,能够有2%-3%的准确度提升
- 网络直接输出各类概率(softmax),比SVM分类器性能略好
- 更多候选窗不能提升性能
同年作者团队又推出了Faster RCNN,进一步把检测速度提高到准实时,可以参看这篇博客。
关于RCNN, Fast RCNN, Faster RCNN这一系列目标检测算法,可以进一步参考作者在15年ICCV上的讲座Training R-CNNs of various velocities。