【目标检测】SPP-Net (Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition)

Posted on   |   In , , , , ,   |   views

K. He, X. Zhang, S. Ren, and J. Sun. Spatial pyramid pooling in deep convolutional networks for visual recognition. In ECCV, 2014.

文章转载于：物体检测论文-SPPNet

Kaiming的这篇paper，是在R-CNN的基础上提出了空间金字塔变换层(Spatial Pyramid Pooling)，SPPNet大幅度提高了R-CNN的训练速度和测试速度，同时算法的精度也上升了，后续的Fast R-CNN、Faster R-CNN模型也是以这个思路，下面就来细致学习SPPNet模型。

1. Introduction

SPPNet主要针对R-CNN模型以下两点提出改进：

  • CNN网络后面接的FC层需要固定的输入大小，限制网络的输入大小
  • 候选区域会塞给CNN网络用于提取特征向量的，这会有大量的重复计算，造成的计算冗余

1.1 为什么CNN需要固定大小的输入?

因为一个CNN一般分为两个部分，前面的部分是卷积层，后面的部分是FC层，卷积层不要求固定大小的输入;但是FC层在设计时就固定了神经元的个数，故需要固定长度的输入。这也就是CNN需要固定输入的问题所在。SPPNet的解决方案如下:

R-CNN模型 SPPNet模型
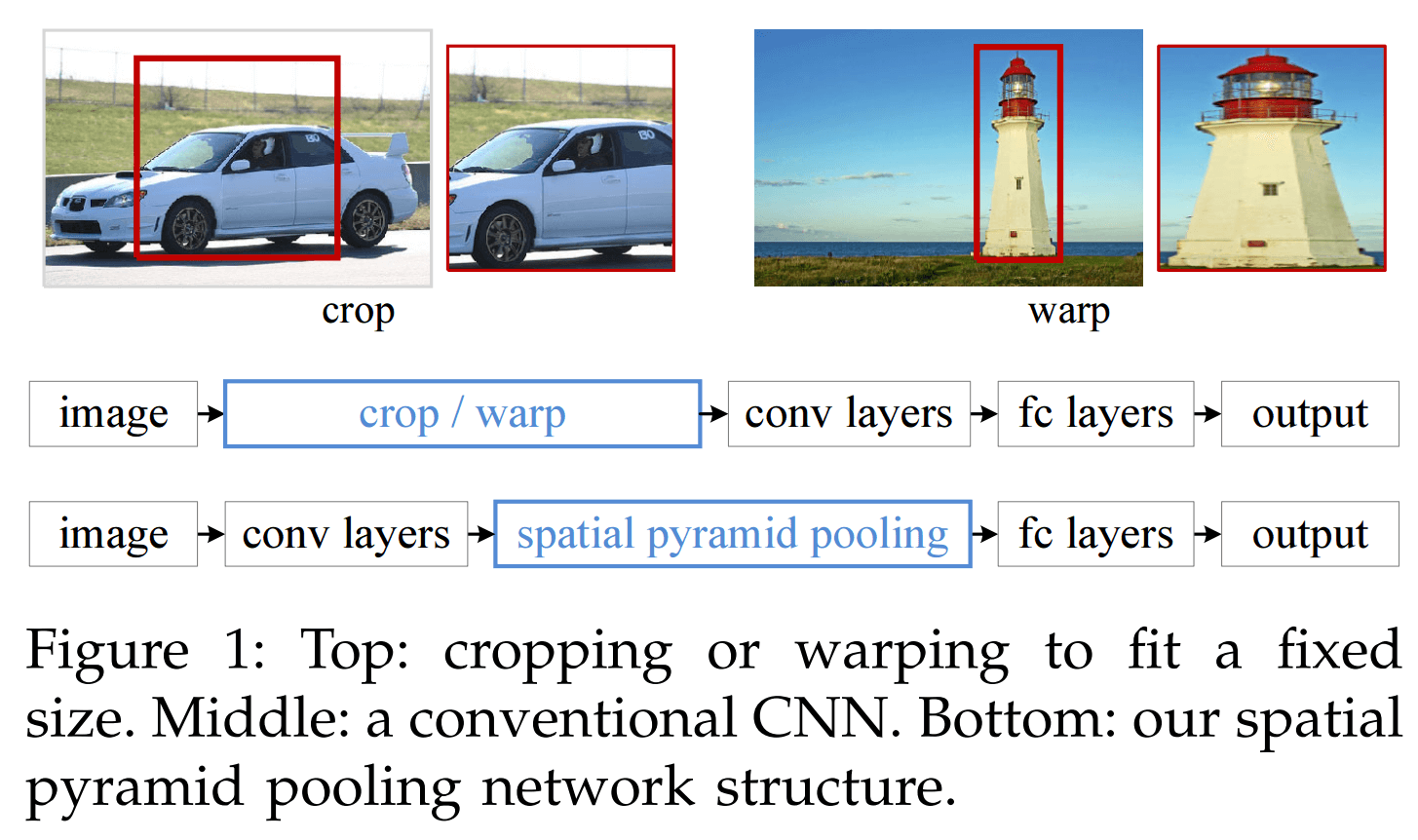
将侯选区域送到CNN里面提取特征向量时，因为CNN的输入图像需要固定大小，而候选区域的长宽都是不固定的，故需要对候选区域做填充到固定大小，当我们对侯选区域做cropping或者warping操作，可能会让图片不完整包含物体，一些我们不想见到的几何失真，这都会造成识别精度损失。 SPPNet的解决办法是使用“空间金字塔变换层”将接收任意大小的图像输入，输出固定长度的输出向量，这样就能让SPPNet可接受任意大小的输入图片，不需要对图像做crop/wrap操作。

2.1 R-CNN模型候选区域在CNN重复计算

R-CNN模型 SPPNet模型
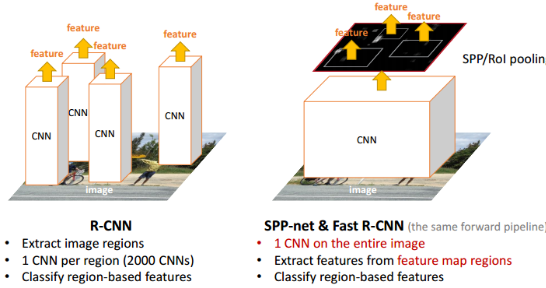
在R-CNN中，每个候选区域都要塞到CNN内提取特征向量，一张图片有2000个候选区域，也就是一张图片需要经过2000次CNN的前向传播，这2000重复计算过程会有大量的计算冗余，耗费大量的时间。 SPPNet提出了一种从候选区域到全图的特征映射(feature map)之间的对应关系，通过此种映射关系可以直接获取到候选区域的特征向量，不需要重复使用CNN提取特征，从而大幅度缩短训练时间。

3.1 我们通俗的理解一下R-CNN和SPPNet的实现过程：

R-CNN模型 SPPNet模型
R-CNN是让每个候选区域经过crop/wrap等操作变换成固定大小的图像

固定大小的图像塞给CNN
CNN输出获得固定大小的feature map
feature map传给后面的层做训练回归分类操作。

这里每个候选区域是需要单独过一下CNN，2000个候选区域过2000次CNN，耗费时间啊		 SPPNet把全图塞给CNN得到全图的feature map
让候选区域与feature map直接映射，得到候选区域的映射特征向量(这是映射来的，不需要过CNN).

映射过来的特征向量大小不固定，所以这些特征向量塞给SPP层(空间金字塔变换层)，SPP层接收任何大小的输入，输出固定大小的特征向量，再塞给FC层

经过映射+SPP转换，简化了计算，速度/精确度也上去了

看完上面的介绍，可以定位这篇论文的两个难点了:

  • SPPNet怎么就能把候选区域从全图的feature map 直接整出来特征向量了？
  • SPP层怎么可以接收任意大小的输入，输出固定的向量？

2. 空间金字塔变换层接收任意大小的输入，输出固定的向量

先了解一下Bag-of-words以及Spatial Pyramid Matching，可以参考如下两篇博客：

第九章三续：SIFT算法的应用—目标识别之Bag-of-words模型
Spatial Pyramid Matching 小结

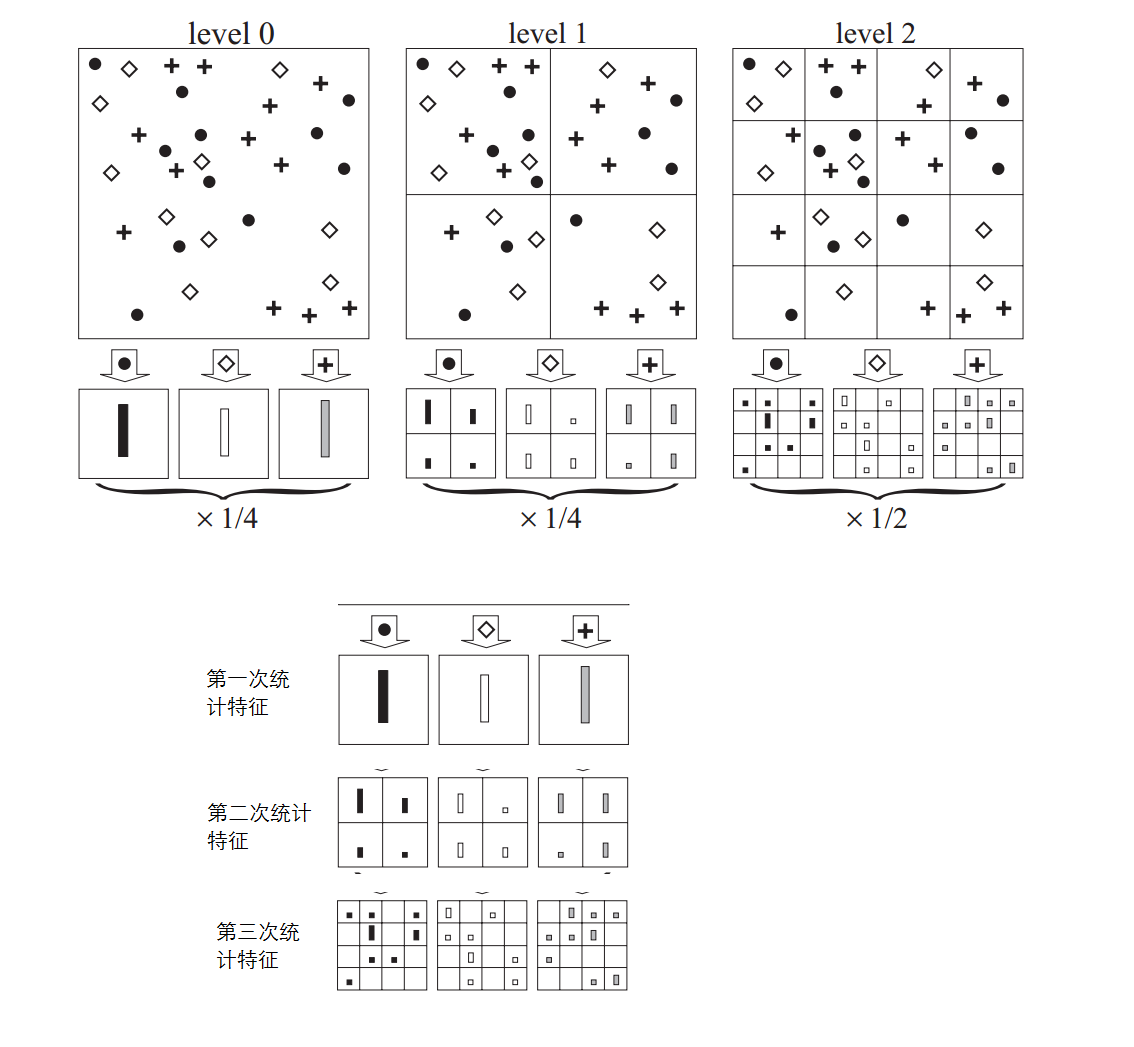
空间金字塔变换层(Spatial Pyramid Pooling,SPP)可以对图片提取特征，例如下图就是1x1，2x2，4x4大小的bin块，将一张图片以三种方式切割并提取特征，这样我们可以得到一共1+4+16=21种特征，这就是以不同的大小的bin块来提取特征的过程就是空间金字塔变换。

不同大小侯选区域在feature map上的映射塞给SPP层上：

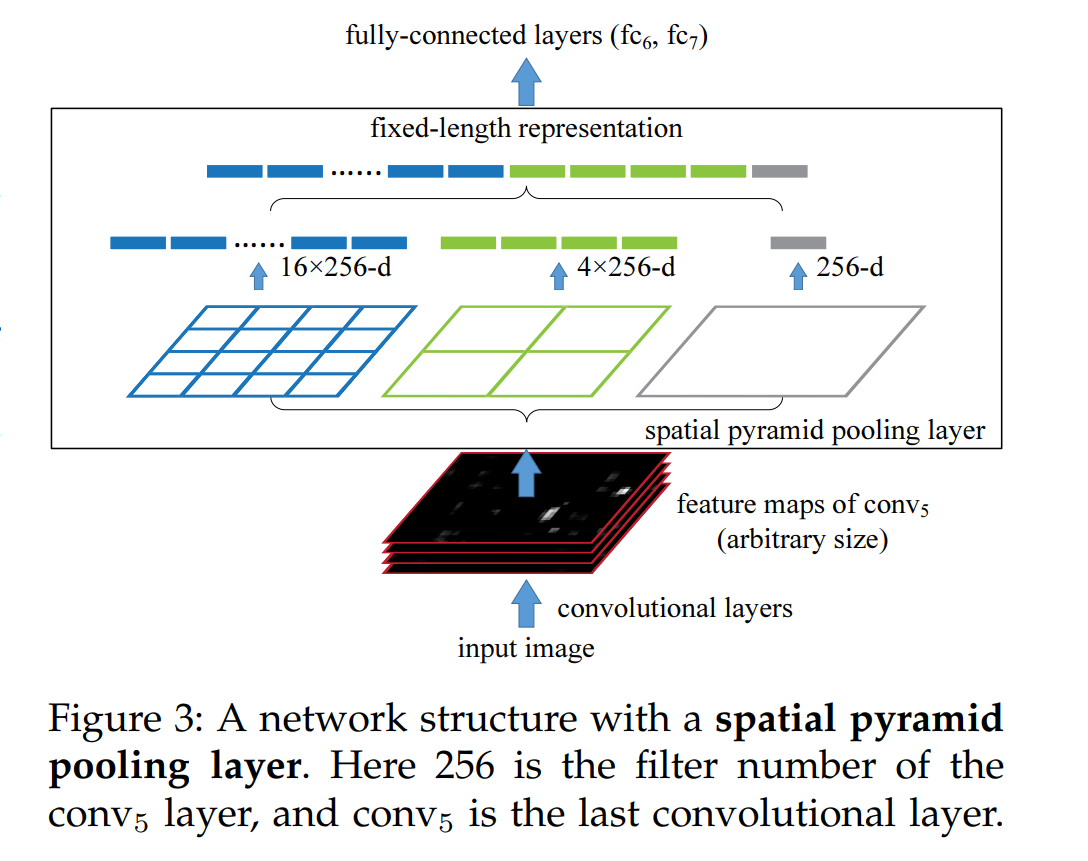
上图spp layer分成1x1(塔底)，2x2(塔中)，4x4（塔顶）三张子图，对每个子图的每个区域作max pooling(论文使用的)，出来的特征再连接到一起，就是(16+4+1)x256的特征向量。

无论输入图像大小如何，出来的特征固定是(16+4+1)x256维度。这样就实现了不管图像尺寸如何，SPP层的输出永远是(16+4+1)x256特征向量。

3. 把候选区域从全图的feature map映射出特征向量

这部分在论文的Appendix A里面简单的介绍了下：

网上查了一堆资料。这里引用知乎-晓雷机器学习笔记。machineLearning-blog. 添加一些自己的理解。

3.1 感受野的计算

感受野我们在CNN里面讲过关于卷积参数计算。

在CNN中感受野(receptive fields)是指某一层输出结果中一个元素所对应的上一层的区域大小.

在卷积参数计算过程中，我们给出上一层/下一层/滤波器尺寸、步长和填充大小的关系:

类型 大小
输入尺寸 \(W1×H1\)
卷积核 \(F×F\)
输出尺寸 \(W2×H2\)
步长 stride：\(S\)
填充大小 padding:\(P\)

关系式如下：
\[ W_2=\frac{W_1−F+2P}{S} + 1, \\ H_2=\frac{H_1−F+2P}{S} + 1 \]
这是上一层到下一层的推导，如果现在反过来，给你下一层的大小，问你上一层的感受野多大，该怎么计算？

我们把上面公式变个形式:
\[ W_1=(W_2−1)S−2P+F \\ H_1=(H_2−1)S−2P+F \]
直观的感受一下从后向前计算感受野的过程

3.2 考虑一下如何计算多层之间的感受野？

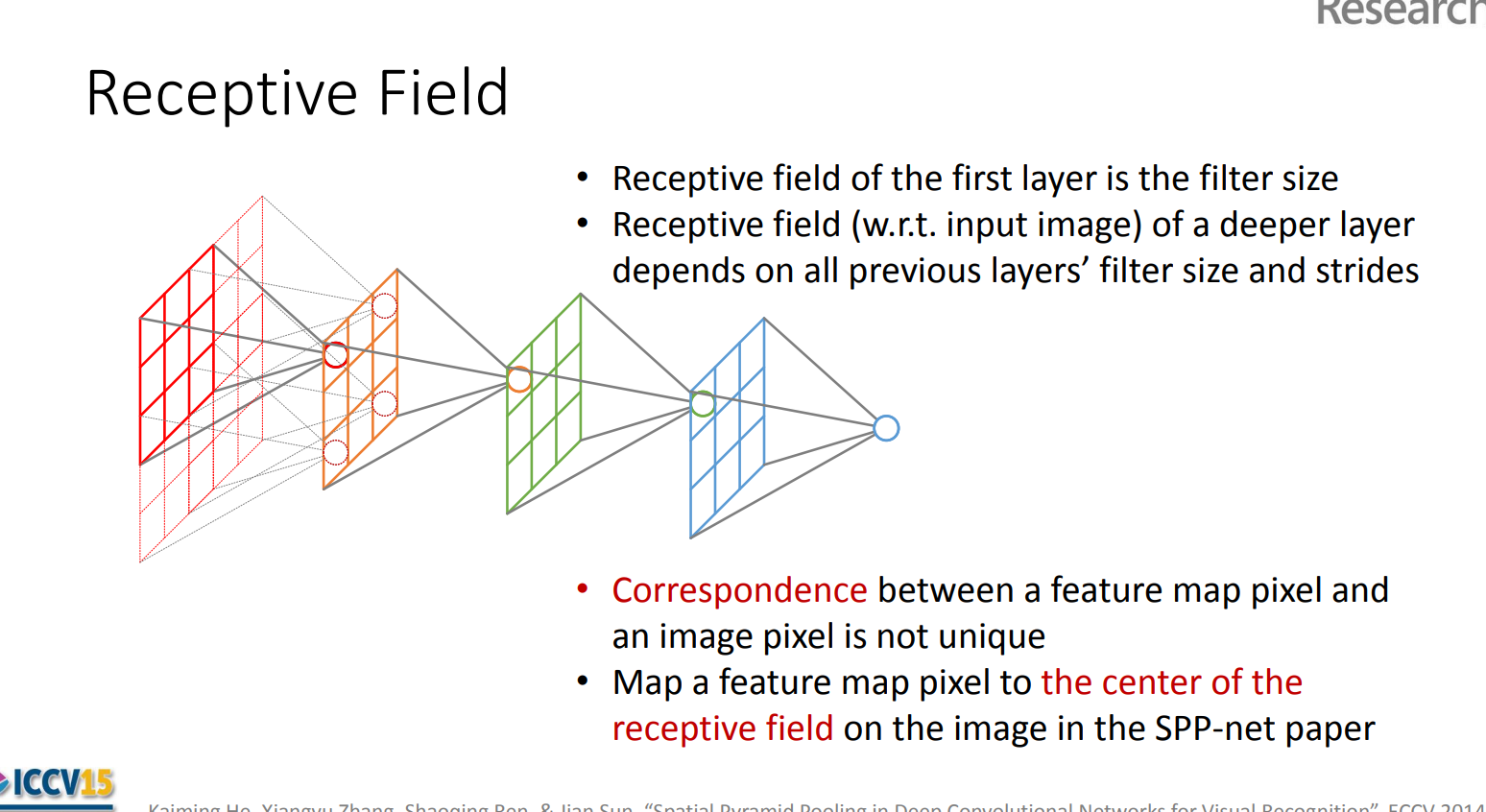
感受野计算时有下面的几个情况需要说明：

  • 第一层卷积层的输出特征图像素的感受野的大小等于滤波器的大小
  • 深层卷积层的感受野大小和它之前所有层的滤波器大小和步长有关系
  • 计算感受野大小时，忽略了图像边缘的影响，即不考虑padding的大小

这里的每一个卷积层还有一个strides的概念，这个strides是之前所有层stride的乘积:
\[ strides_i=stride_1⋅stride_2⋅⋅⋅stride_{i−1} \]
关于感受野大小的计算采用down to top的方式: 即先计算最深层在前一层上的感受野，然后逐渐传递到第一层，使用的公式可以表示如下：

例如我们计算AlexNet的第四层到第一层的感受野:

下面是一个程序计算了AlexNet、VGG16、ZF-5的输入输出尺寸的变化和感受野变化过程，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#!/usr/bin/env python

net_struct = {'alexnet': {'net':[[11,4,0],[3,2,0],[5,1,2],[3,2,0],[3,1,1],[3,1,1],[3,1,1],[3,2,0]],
                   'name':['conv1','pool1','conv2','pool2','conv3','conv4','conv5','pool5']},
       'vgg16': {'net':[[3,1,1],[3,1,1],[2,2,0],[3,1,1],[3,1,1],[2,2,0],[3,1,1],[3,1,1],[3,1,1],
                        [2,2,0],[3,1,1],[3,1,1],[3,1,1],[2,2,0],[3,1,1],[3,1,1],[3,1,1],[2,2,0]],
                 'name':['conv1_1','conv1_2','pool1','conv2_1','conv2_2','pool2','conv3_1','conv3_2',
                         'conv3_3', 'pool3','conv4_1','conv4_2','conv4_3','pool4','conv5_1','conv5_2','conv5_3','pool5']},
       'zf-5':{'net': [[7,2,3],[3,2,1],[5,2,2],[3,2,1],[3,1,1],[3,1,1],[3,1,1]],
               'name': ['conv1','pool1','conv2','pool2','conv3','conv4','conv5']}}

imsize = 224

def outFromIn(isz, net, layernum):
    totstride = 1
    insize = isz
    for layer in range(layernum):
        fsize, stride, pad = net[layer]
        outsize = (insize - fsize + 2*pad) / stride + 1
        insize = outsize
        totstride = totstride * stride
    return outsize, totstride

def inFromOut(net, layernum):
    RF = 1
    for layer in reversed(range(layernum)):
        fsize, stride, pad = net[layer]
        RF = ((RF -1)* stride) + fsize
    return RF

if __name__ == '__main__':
    print "layer output sizes given image = %dx%d" % (imsize, imsize)
    
    for net in net_struct.keys():
        print '************net structrue name is %s**************'% net
        for i in range(len(net_struct[net]['net'])):
            p = outFromIn(imsize,net_struct[net]['net'], i+1)
            rf = inFromOut(net_struct[net]['net'], i+1)
            print "Layer Name = %s, Output size = %3d, Stride = % 3d, RF size = %3d" % (net_struct[net]['name'][i], p[0], p[1], rf)

执行结果如下：

3.3 基于感受野的特征映射

通常，我们需要知道网络里面任意两个feature map之间的坐标映射关系（一般是中心点之间的映射），如下图，我们想得到map 3上的点p3映射回map 2所在的位置p2（橙色框的中心点）

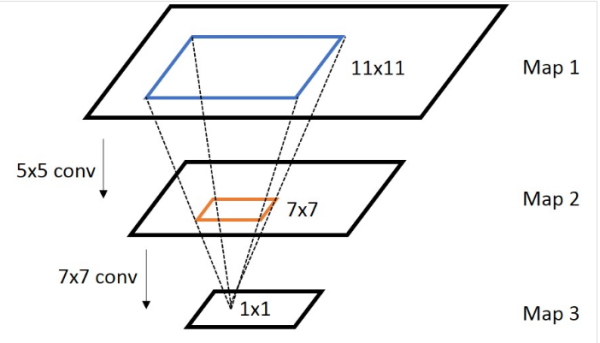
计算公式：

  • 对于 \(Conv/Pool layer: p_i=s_i⋅p_{i+1}+((k_i−1)/2−padding)\)
  • 对于\(Neuron layer(ReLU/Sigmoid/..) : p_i=p_{i+1}\)

上面是计算任意一个layer输入输出的坐标映射关系，如果是计算任意feature map之间的关系，只需要用简单的组合就可以得到，下图是一个简单的例子:

下图是Kaiming He 在ICCV15上的汇报用的PPT，讲解如何求解Receptive Field:

  • A simple solution：
    何凯明在SPP-net中采用的方法。巧妙的化简一下公式
    \[ p_i=s_i⋅p_{i+1}+((k_i−1)/2−padding) \]
    令每一层的padding都为
    \[ padding=⌊k_i/2⌋ \ \ \ ⇒ \ \ \ p_i=s_i⋅p_{i+1}+((k_i−1)/2−⌊k_i / 2⌋) \]

  • 当 \(k_i\) 为奇数时：
    \[ (k_i−1)/2−⌊k_i/2⌋)=0 \ \ \ ⇒ \ \ \ p_i=s_i ⋅ p_{i+1} \]

  • 当 \(k_i\) 为偶数时：
    \[ ((k_i−1)/2−⌊k_i/2⌋)=−0.5 \ \ \ \ ⇒ \ \ \ p_i=s_i⋅p_{i+1}−0.5 \]

  • 而 \(p_i\) 是坐标值，不取小数，基本上认为 \(p_i=s_i⋅p_{i+1}\) 。感受野中心点的坐标\(p_i\)只跟前一层 \(p_{i+1}\)有关。

  • A general solution:
    其实就是把公式 \(p_i=s_i⋅p_{i+1}+((k_i−1)/2−padding)\) 级联消去整合一下

3.4 候选区域到feature map的映射做法详解

SPP-net 是把原始ROI的左上角和右下角 映射到 feature map上的两个对应点。 有了feature map上的两对角点就确定了 对应的 feature map 区域(下图中橙色)。


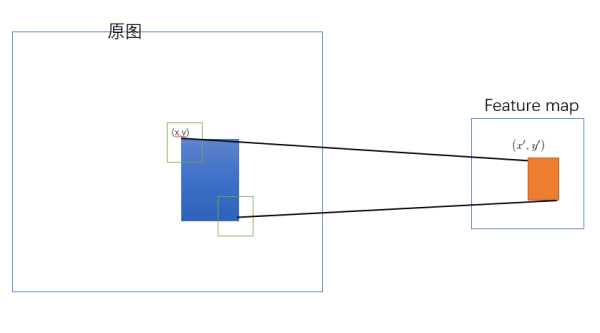
如何映射？
左上角的点\((x,y)\)映射到 feature map上的\((x′,y′)\) : 使得\((x′,y′)\) 在原始图上感受野（上图绿色框）的中心点与\((x,y)\)尽可能接近。

3.5 对应点之间的映射公式是啥？

  • 就是前面每层都填充 \(padding/2\) 得到的简化公式 \(p_i=s_i⋅p_{i+1}\)
  • 需要把上面公式进行级联得到 \(p_0=S⋅p_{i+1}\) 其中 \((S=\prod^i_0s_i)\)
  • 对于feature map 上的\((x′,y′)\) 它在原始图的对应点为 \((x,y)=(Sx′,Sy′)\)
  • 论文中的最后做法：把原始图片中的ROI映射为 feature map中的映射区域（上图橙色区域）
  • 左上角取： \(x′=⌊x/S⌋+1\) ; \(y′=⌊y/S⌋+1\)
  • 右下角取： \(x′=⌈x/S⌉−1\) ; \(y′=⌈y/S⌉−1\)

4. 总结

到这里就算是把SPPNet的核心思想讲完了，SPPNet网络后面和R-CNN类似，训练SVM分类器和位置回归等。 SPPNet在R-CNN的基础上提出了改进，通过候选区域和feature map的映射，配合SPP层的使用，从而达到了CNN层的共享计算，减少了运算时间。后面的Fast R-CNN也是受SPPNet的启发，一次又一次的刷新物体检测的state-of-the-art。

5. Reference: