SVM本身是一个二值分类器。SVM算法最初是为二值分类问题设计的,当处理多类问题时,就需要构造合适的多类分类器。目前,构造SVM多类分类器的方法主要有两类:直接法 和 间接法。
1. 直接法
直接在目标函数上进行修改,将多个分类面的参数求解合并到一个最优化问题中,通过求解该最优化问题“一次性”实现多类分类。这种方法看似简单,但其计算复杂度比较高,实现起来比较困难,只适合用于小型问题中。
2. 间接法
主要是通过组合多个二分类器来实现多分类器的构造,常见的方法有 one-against-one 和 one-against-all 两种。
2.1 一对多法(one-versus-rest 简称OVR SVMs)
训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类,这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。
例如:假如我有四类要划分(也就是4个label),他们是A、B、C、D。
于是我在抽取训练集的时候,分别抽取
(1)A所对应的向量作为正集,B,C,D所对应的向量作为负集;
(2)B所对应的向量作为正集,A,C,D所对应的向量作为负集;
(3)C所对应的向量作为正集,A,B,D所对应的向量作为负集;
(4)D所对应的向量作为正集,A,B,C所对应的向量作为负集;
使用这四个训练集分别进行训练,然后的得到四个训练结果文件。
在测试的时候,把对应的测试向量分别利用这四个训练结果文件进行测试。最后每个测试都有一个结果 \(f1(x),f2(x),f3(x),f4(x)\) 于是最终的结果便是这四个值中最大的一个作为分类结果。
评价:这种方法有种缺陷,训练数据集不平衡,因而不是很实用。可以在抽取数据集的时候,从完整的负集中再抽取三分之一作为训练负集。
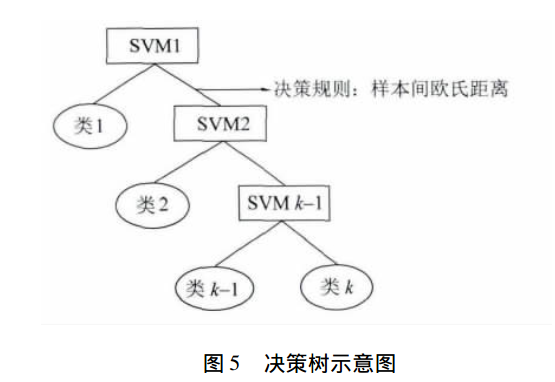
2.2 基于决策树的SVMs(ST-SVMs)层次支持向量机
从“一对多”的方法又衍生出基于决策树的分类:首先将所有类别分为两个类别,再将子类进一步划分为两个次级子类,如此循环下去,直到所有的节点都只包含一个单独的类别为止,此节点也是二叉树树种的叶子。该分类将原有的分类问题同样分解成了一系列的两类分类问题,其中两个子类间的分类函数采用SVM。如下图表示:
2.3 一对一法(one-versus-one 简称OVO SVMs)
其做法是在任意两类样本之间设计一个SVM,因此 \(k\) 个类别的样本就需要设计 \(k(k-1)/2\) 个SVM。当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别,这种策略称为”投票法“。libsvm 中的多类分类就是根据这个方法实现的。
例如:假设有四类A,B,C,D四类。在训练的时候我们选择(A,B)、 (A,C)、(A,D)、(B,C)、(B,D)、(C,D)所对应的向量作为训练集,然后得到六个训练结果,在测试的时候,把对应的向量分别对六个结果进行测试,然后采取投票形式,最后得到一组结果。投票是这样的:
A=B=C=D=0; # 票数初始化
(A,B)-classifier 如果是A win,则A=A+1;otherwise, B=B+1;
(A,C)-classifier 如果是A win,则A=A+1;otherwise, C=C+1;
…
(C,D)-classifier 如果是A win,则C=C+1;otherwise, D=D+1;
The decision is the Max(A,B,C,D)
评价:这种方法虽然好,但是当类别很多的时候,model的个数是 \(n*(n-1)/2\) ,代价还是相当大的。
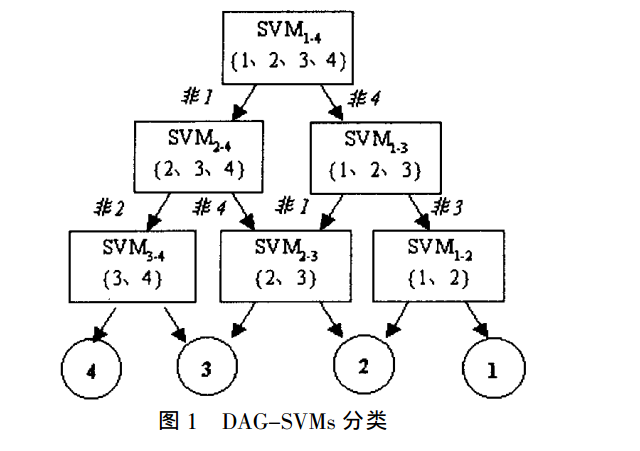
2.4 有向无环图SVMs(Directed Acyclic Graph SVMs)
从”一对一“衍生出来的,其在训练阶段和”1-1“投票一样,也要构造出每两类间的分类面,即有 \(k(k - 1)/2\) 个分类器。但是在分类阶段,该方法将所用分类器构造成一种两向有向无环图(图1):包括 \(k(k - 1)/2\) 个节点和 \(k\) 个”叶“。其中每个节点为一个分类器,并与下一层的两个节点(或者叶)相连。当对一个未知样本进行分类时,首先从顶部的根节点开始,根据根节点的分类结果用下一层中的左节点或者右节点继续分类,知道到达底层某个叶为止,该叶所表示的类别即未知样本的类别。
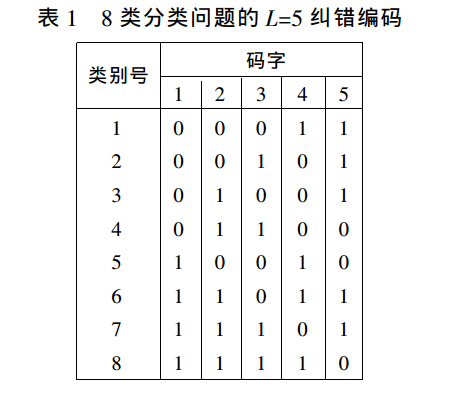
2.5 纠错编码 SVMs
Dietterich 提出对类别进行二进制编码将多类分类问题转化为多个两类分类问题。对于 \(k\) 类分类问题,给每个类别赋予一个长度为L的二进制编码,形成一个 \(k\) 行 \(L\) 列的码本(表1)对于其中第 \(i (=1,..,L )\) 列,将该位中码字为 ”0” 的所有类别作为一类,其他码字为 “1” 的类别归为另一类,因此每个码位对应一个两类分类问题,\(k\) 类分类问题就转化为 \(L\) 个两类分类问题。采用具有纠错能力的编码对类别进行编码,并将SVM作为码位分类器,这种多类SVM分类方法被称为纠错编码支持向量机(ECC -SVM)。对于一个未知样本分类时,\(L\) 个SVM分类器的分类结果(0或1 )构成一个编码 \(s\) ,计算码本内 \(k\) 个编码与 \(s\) 汉明距离,距离最小者所代表的类别即该测试样本所属类别。
3. Reference
[1] 刘志刚,李德仁,秦前清,史文中.支持向量机在多类分类问题中的推广[J].计算机工程与应用,2004(07):10-13+65.
[2] 王正海,方臣,何凤萍,祖玉川,王磊,王娟.基于决策树多分类支持向量机岩性波谱分类[J].中山大学学报(自然科学版),2014,53(06):93-97+105.
[3] Multi-Class Support Vector Machine
[4] https://www.cnblogs.com/CheeseZH/p/5265959.html
[5] https://blog.csdn.net/xfChen2/article/details/79621396
[6] https://blog.csdn.net/rainylove1/article/details/32101113