Contrastive loss 最初源于
Yann LeCun“Dimensionality Reduction by Learning an Invariant Mapping” CVPR 2006。该损失函数主要是用于降维中,即本来相似的样本,在经过降维(特征提取)后,在特征空间中,两个样本仍旧相似;而原本不相似的样本,在经过降维后,在特征空间中,两个样本仍旧不相似。同样,该损失函数也可以很好的表达成对样本的匹配程度。
1. Contrastive Loss 定义
在caffe的孪生神经网络(siamese network)中,其采用的损失函数是 contrastive loss,这种损失函数可以有效的处理孪生神经网络中的paired data的关系。contrastive loss 的表达式如下:
\[
L(W, (Y, X_1, X_2))=\frac{1}{2N}\sum_{n=1}^N \left( YD_W ^2+(1-Y)max(m-D_W,0)^2 \right)
\]
其中 \(D_W(X_1, X_2)=||X_1 - X_2||_2 = (\sum^P_{i=1}{(X^i_1 - X^i_2)^2})^\frac{1}{2}\),代表两个样本特征 \(X_1\) 和 \(X_2\) 的欧氏距离(二范数)\(P\) 表示样本的特征维数,\(Y\) 为两个样本是否匹配的标签,\(Y=1\) 代表两个样本相似或者匹配,\(Y=0\) 则代表不匹配,\(m\) 为设定的阈值,\(N\) 为样本个数。
观察上述的contrastive loss的表达式可以发现,这种损失函数可以很好的表达成对样本的匹配程度,也能够很好用于训练提取特征的模型。
当 \(Y = 1\)(即样本相似时),损失函数只剩下 \(L_S = \frac{1}{2N}\sum_{n=1}^NYD_W ^2\) ,即原本相似的样本,如果在特征空间的欧式距离较大,则说明当前的模型不好,因此加大损失。
当 \(Y = 0\)(即样本不相似时),损失函数为 \(L_D = \frac{1}{2N}\sum_{n=1}^N (1-Y)max(m-D_W,0)^2\) ,即当样本不相似时,其特征空间的欧式距离反而小的话,损失值会变大,这也正好符号我们的要求。
[注意这里设置了一个阈值 margin,表示我们只考不相似特征欧式距离在0~margin 之间的,当距离超过 margin 的,则把其 loss 看做为0(即不相似的特征离的很远,其 loss 应该是很低的;而对于相似的特征反而离的很远,我们就需要增加其 loss,从而不断更新成对样本的匹配程度)]
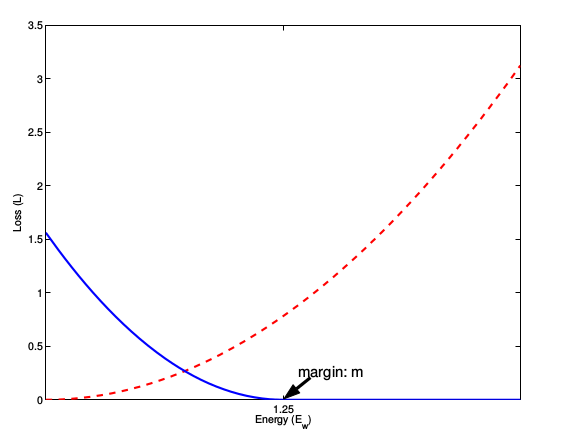
这张图表示的就是损失函数值与样本特征的欧式距离之间的关系,其中红色虚线表示的是相似样本的损失值,蓝色实线表示的不相似样本的损失值。
2. 梯度计算
论文中使用 stochastic gradient descent 来不断更新 \(D_W\),不断减小 loss,更好表达成对样本的匹配程度。
- \(Y = 1\)(即样本相似时),损失函数为 \(L_S = \frac{1}{2N}\sum_{n=1}^ND_W ^2\) ,此时计算梯度为:
\[ \frac{\partial L_S}{\partial W} = D_W\frac{\partial D_W}{\partial W} \\ \]
即分别对 \(X_1\)和\(X_2\)求偏导,更新梯度 :
\[ \frac{\partial L_S}{\partial W} = \left\{ \begin{eqnarray} &&\frac{\partial L_S}{\partial X_1} = D_W\frac{\partial D_W}{\partial X_1} = D_W\frac{\partial}{\partial X_1} ||X_1 - X_2||_2 = D_W\frac{ X_1-X_2}{||X_1-X_2||_2} = X_1 - X_2 \\ &&\frac{\partial L_S}{\partial X_2} = D_W\frac{\partial D_W}{\partial X_2} = D_W\frac{\partial}{\partial X_2} ||X_1 - X_2||_2 = D_W\frac{ -(X_1-X_2)}{||X_1-X_2||_2} = -(X_1 - X_2) \end{eqnarray}\right. \]
- \(Y = 0\) (即样本不相似时),损失函数为 \(L_D = \frac{1}{2N}\sum_{n=1}^N (1-Y)max(m-D_W,0)^2\),此时计算梯度为 :
\[ \frac{\partial L_D}{\partial W} = \left\{ \begin{matrix} &0 &, D_W > m \\ &-(m - D_W)\frac{\partial D_W}{\partial W} &, D_W < m \end{matrix}\right. \]
同理,当\(D_W < m\)时,分别对 \(X_1\) 和 \(X_2\) 求偏导:
\[ \frac{\partial L_D}{\partial W} = \left\{\begin{eqnarray} &&\frac{\partial L_D}{\partial X_1} = -(m - D_W)\frac{\partial D_W}{\partial X_1} = -(m - D_W)\frac{\partial}{\partial X_1} ||X_1 - X_2||_2 = -(m - D_W)\frac{ X_1-X_2}{||X_1-X_2||_2} = -(m - D_W)\frac{ X_1-X_2}{D_W} \ \\ &&\frac{\partial L_D}{\partial X_2} = -(m - D_W)\frac{\partial D_W}{\partial X_2} = -(m - D_W)\frac{\partial}{\partial X_2} ||X_1 - X_2||_2 = -(m - D_W)\frac{ -(X_1-X_2)}{||X_1-X_2||_2} = -(m - D_W)\frac{ -(X_1-X_2)}{D_W} & \end{eqnarray}\right. \]
3. Spring Model Analogy 弹簧模型类比
弹簧模型公式:
\[
F = -KX
\]
( \(F\) 表示两点间弹簧的作用力,\(K\) 是弹簧的劲度系数,\(X\) 为弹簧拉伸或收缩的长度,弹簧静止状态时 \(X=0\) )
论文中将该 contrastive loss 损失函数类比于弹簧模型:将成对的样本特征,使用该损失函数来表达成对样本特征的匹配程度。成对的样本特征之间(类比于图中的一个个点),我们假设这些点之间都有一个弹簧,弹簧静止时长度为0,点对之间无作用力。①对于样本相似的特征,相当于其间的弹簧产生了正位移 \(X(X < m)\),即弹簧被拉伸了 \(X\) 的长度,此时两个相似特征(点)之间存在吸引力。②对于样本不相似的特征,相当于其间的弹簧产生的了负位移,即弹簧被压缩了,此时两个不相似特征之间存在排斥力。注意弹簧的特性:当两点之间弹簧位移超\(X>m\) 时,此时,弹簧发生形变,此时两点之间视为没有吸引力了。具体如下图所示:
结合上面求梯度的公式也可以很好的理解该损失函数的思想,上面的 \(\frac{\partial L_S}{\partial W}\) 和 \(\frac{\partial L_D}{\partial W}\) 代表两点间弹簧的作用力 \(F\),\(\frac{\partial D_W}{\partial W}\) 对应弹簧的劲度系数,\(D_W\) 和 \(-(m - D_W)\) 代表弹簧的缩放位移。
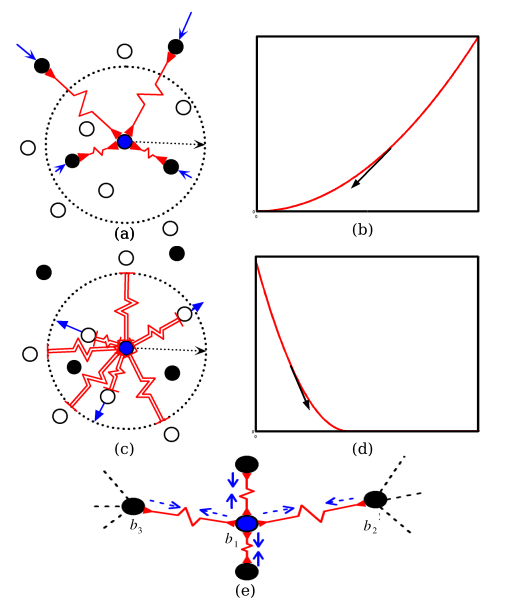
上图显示了类比的弹簧系统。实心圆表示与中心点相似的点。空心圆圈代表不同的点。弹簧显示为红色曲折线。作用在点上的力以蓝色箭头显示。箭头的长度近似给出了力的强度。在右侧的两个图中,x轴是距离 \(D_W\),y轴是损失函数的值。(a)中显示使用仅吸引attractonly弹簧连接到相似点的点。(b)表示相似点对的损失函数及其梯度。(c)表示该点仅与半径为m的圆内的不同点连接,仅具有m-repulse-only排斥弹簧连接到不相似的点。(d)显示不相似点对相关的损失函数及其梯度。(e)显示一个点被不同方向的其他点拉动,形成平衡的情况。